
Photo by
cheemamericco
Pythonを用いた機械学習18日目
第4章の関数と微分をいっきに学習していく。
1.関数
関数には、一次関数、二次関数、指数関数や三角関数がある。これらに共通するのは、入力値を1つ決めると、出力が1つ決まること。
*y=2x+1という一次関数を実装したコード
>>> def func(x):
... return 2 * x + 1
...
>>> print(func(-2))
-3
>>> print(func(1))
3
2.微分
*hを0に近づけて微分係数の変化を見るコード
>>> def f(x):
... return x ** 2
...
>>> def df(x, h):
... return (f(x + h) - f(x)) / h
...
>>> for h in [1, 1e-1, 1e-2, 1e-3]:
... print([h, df(0, h), df(1, h)])
...
[1, 1.0, 3.0]
[0.1, 0.10000000000000002, 2.100000000000002]
[0.01, 0.01, 2.0100000000000007]
[0.001, 0.001, 2.0009999999996975]上記のdfを以下のように定義すると、誤差が少なくなる。
def df(x, h):
return (f(x + h) - f(x - h)) / (2 * h)*連鎖律・・・複数の関数からなる合成関数の導関数は、それぞれの導関数を掛け算して求められる。
NumPyのexp関数を使ってシグモイド関数を定義し、以下のようにその導関数もかんたんに実装できる。
*シグモイド関数とその微分を計算するコード
>>> def sigmoid(x):
... return 1.0 / (1.0 + np.exp(-x))
...
>>> def sigmoid_derivative(x):
... return sigmoid(x) * (1 - sigmoid(x))3.多変数関数で最小値を求める
*小さく移動を繰り返して最小値に近づけるコード
>>> def f(x, y):
... return x * x + y * y
...
>>> def dfx(x, y):
... return 2 * x
...
>>> def dfy(x, y):
... return 2 * y
...
>>> eta = 0.1
>>> x, y = 10, 8
>>> print(f(x, y))
164
>>>
>>> for i in range(0, 30):
... x += - eta * dfx(x, y)
... y += - eta * dfy(x, y)
... print(f(x, y))
...
104.96000000000001
67.1744
42.991616
27.51463424
17.6093659136
11.269994184704004
7.212796278210563
4.616189618054761
2.9543613555550463
1.89079126755523
1.2101064112353472
•••4.練習問題
⑦連鎖律を使って以下の関数を微分する(公式の確認問題?)
(1)
![]()
解答:
![]()
(2)
![]()
解答:
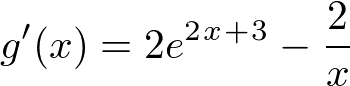
(3)
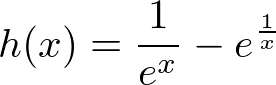
解答:
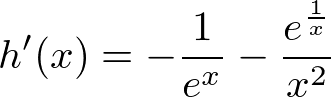
⑧以下の関数をx, yそれぞれで偏微分する(公式の確認問題?)
(1)
![]()
解答:
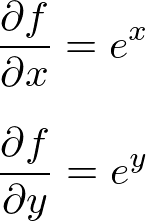
(2)
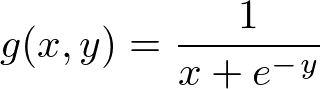
解答:
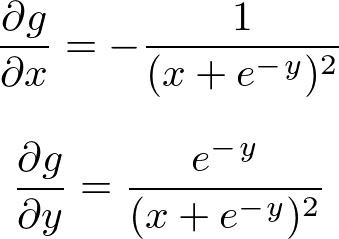
(3)
![]()
解答:
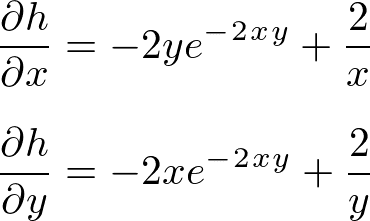
次回から、ここまで学習してきた数学的な知識を使って実際に予測する方法と、ニューラルネットワークで使われる誤差逆伝播の考えかたについて学んでいく。
いいなと思ったら応援しよう!

