
パズルの解の数を調べるには
本日の話題
前の記事では、一筆書きには二種類あって、そのうち点の一筆書きは「NP完全」という性質で、解くことが難しいとされていることをご紹介したわ。
NP完全や、P対NPについてのざっくりした解説は下記が参考になりそうよ。
このnoteでNP完全について言及してもいいけれど、かなり難しい(私も詳しく覚えていない)から、やめておくわ。それに、探せばいろんな方が解説記事を作っているしね。
今日は、点の一筆書きという「パズル」らしさを追求したテーマにしたいと思うの。ずばり、内容はずばり「パズルの答えを1通りにしたい」!比較的簡単だからついてきてくれると幸いよ。
なぜ1通り?
まずは、次の敷き詰めパズルから考えてみよっか。

敷き詰め方は何通り?
答えは2通りあるわね!
でも、数独とかを解いているときって、答えが1通りしかないよね?
数独の答えって、なんで1通りなのかしら?
まず答えが0通り、つまり解がないと、そもそもパズルの問題として成立しないっか。
複数答えがあるとしたらどうなるかしら。数独って、論理的に確定するマスを、数字で埋めていくのよね。答えが複数あった場合って、過程のどこかで確定できないマスができてしまうんじゃないかしら?
なんか適当にあてはめたら、たまたまうまくいっちゃった~というのは、うれしいけれど何かしっくりこないよね、そう思いません?だから、全部論理的に決めるためにも、暗黙の了解で、答えは1通りでなければならないルールがあると思うのよ。
じゃあ「点の一筆書き」はどんな条件だと答えが1通りになるかな?
余談:ASPとは
パズルが別解を持つかどうかという問題は、ASP (Another Solution Problem ) と呼ばれているわ。
http://www.mountainvistasoft.com/docs/puzcc.pdf
点の一筆書き問題は、そもそも経路があるかどうかすら難しいんだから、解が1個かどうかを求めるのはなおさら難しいはずね。
解の個数を証明できる方法はある
でも、一般的な形ではなく、例題に対してなら、次のような証明方法は考えられるわ。
解がないことを示せる例

以降、一筆書きする図はつながっているものとする。

終点に戻るには、点Pを二度通る必要がある。

点Pから戻ることができない。
上のような場合には、一筆書きができないよ。でも注意してほしいのは、それ以外の場合でも一筆書きできない例はたくさんあるということ。つまり、ここで挙げた例は、一筆書きができないための十分条件であって、必要条件ではないこと。一筆書きできないことを判定するための一般的な性質ではないのよ。
解が1個だけであることを示せる例
ここの後半「点の一筆書きの解法?」では、確定できる経路を順に見つけて、最後に1個だけ答えが見つかったね。
解が複数存在することが示せる例
解の個数がわからなくても、1個だけじゃないことを証明できる場合があるよ!

仮に、この図の一筆書きが次の図のような経路だけだったとしようか。

終点にはもう1本、経路に含まれない線がついているわね。これを追加してみると、経路の中にループができるのよ。このループから、別の線を1本うまく選んでやるの。
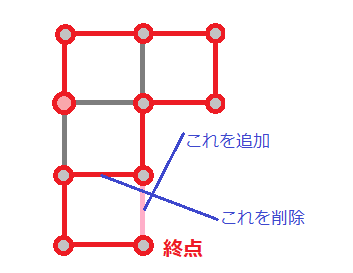
すると、どう?別の一筆書きが現れたわね!!
ということは、一筆書きの解が二つあったってことね!
終点につながっている点に線が二本以上つながっていたから、もう1つの一筆書きを発見できたけれど……、これって、どの点も線が2本つながっている盤面には複数の解答があるってことよね?裏を返せば……。
~ 終点確定定理 ~
点の一筆書きで出発点が決まっているとき、解を1通りにするには、次数1の点がただ1つ存在し、それが一筆書きの終点になる。
点につながっている線の本数を、その点の次数 (Degree) というから、グラフ理論を勉強するなら覚えておくといいわ!
一般的な証明手段
一般的に、解が複数あるのではないかという疑問を解決したいときは、次の手段が使えそうね。
~ 目的物がN個以上存在することを示す ~
N-1 個しかないと仮定したときに、なんやかんや操作をすることで数え上げられていない別の目的物がでてきてしまうので、N個存在してしまう。
免責
※当記事の解説は、筆者の備忘録を分かりやすさ重視で書いているため、表現があいまいだったり厳密でなかったりします。なるべく文献は探しますが、当記事の内容を直ちに受けとめず、真実は必ずご自身でご確認ください(なので、当記事を参考文献にされることは推奨しません)。
次回は、点の一筆書きを「数学で表現するとどうなるか」について書きたいと考えています。
