未解決の超難問「ABC予想」を証明 “天才数学者”望月新一とは何者か？

京都大学数理解析研究所教授の望月新一氏（51）による「宇宙際タイヒミュラー（IUT）理論」についての論文が、数学の専門雑誌『PRISM（プリムス）』に掲載されることが、4月3日に発表された。これによって、35年にわたり未解決だった数学の超難問「ABC予想」が証明されたこととなる。

望月氏は東京都生まれ。5歳の時に渡米し、16歳で米国の名門プリンストン大学に飛び級入学、32歳という若さで京都大学教授に就任という経歴を持つ。

東京工業大学教授の加藤文元氏（51）は、望月氏と20年来の友人であり、IUT理論の構築の過程で議論を重ねた経験も持つ。著書は、IUT理論を一般向けに説明した『宇宙と宇宙をつなぐ数学』（KADOKAWA）、『数学する精神』（中公新書）など多数。

そんな加藤氏が、望月氏の数学者としての凄さを解説する。

加藤氏　©山本彩乃

アインシュタインに喩えられるインパクト

望月新一さんが構築された「宇宙際タイヒミュラー（IUT）理論」によって、数学の未解決難問であり続けた「ABC予想」が証明され、大きな話題になりました。

もちろん「ABC予想」の証明は凄いことですが、IUT理論の構築こそが望月さんの偉大な功績です。言ってしまえば望月さんは、これまでにない“全く新しい数学”を創造したということになるのです。

IUT理論はあまりに独創的で斬新であるため、その内容を正しく理解している数学者は世界でも限られた数しか存在しません。「未来からやってきた論文」と称されたこともあります。

このインパクトについては、アインシュタインの一般相対性理論に喩えられます。一般相対性理論はかなり時代を先取りしていたため、提案された当初はほとんど理解されませんでした。言ってみれば、一般相対性理論は当時、まだ誰もかかったことがない病気に対する薬みたいなものだったのです。IUT理論も似たところがあると言えます。

ここまでの説明だけで匙を投げたくなる方も多いでしょう。ですが実は、IUT理論のアイデアはとても自然な考え方に根差しているのです。皆さんにはその雰囲気に少しでも触れていただければと思います。

望月氏（京都大学提供）

宇宙と宇宙をつなぐ数学 IUT理論の衝撃

数学する精神―正しさの創造、美しさの発見 (中公新書 1912)

はじめに強調しておきたいのは、IUT理論は本来、「ABC予想」を解くためだけに作られたものではないという点です。

望月さんが意図したことは、新しい数学のやり方を開発するための壮大な枠組みを作るということでした。そして、この理論が非常に強力な理論だと証明するための“試金石”が「ABC予想」という流れだったのです。

まずは、「ABC予想」についておおまかに説明します。

「ABC予想」の理解には、中学や高校で習った「素数」と「素因数分解」の知識があれば十分です。少しおさらいすると、どんな自然数もいくつかの素数の積の形に分解できます。例えば、24という数字を見てみましょう。24は6と4のかけ算でつくれます。さらに、6は2と3のかけ算、4は2と2のかけ算に分解することができます。以上から、24＝6・4＝2・3・2・2と素因数分解できるのです。これを累乗の記号を用いて見やすく書くと、

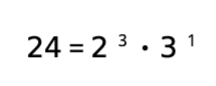
となります。

たし算とかけ算を比べる

それに加えて、自然数の「根基」の概念について説明します。

一般に、自然数ｎについて、それを素因数分解し、そこに現れる素数の指数を全て1にしたものをｎの根基と呼び、rad（n）と書きます。

実際に数を当てはめてやってみましょう。先ほどの24を素因数分解すると、

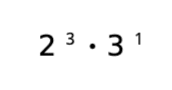
となりました。24の根基は、素因数の指数を全て1にして計算します。2の右肩の数字3と、3の右肩の数字1を全て1にすると、

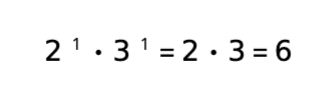
となるため、rad（24）=6です。

本題に入りましょう。「ABC予想」の出発点は、「a＋b＝c」を満たす互いに素な自然数a、b、cについて、その根基を計算することから始まります。

下の枠内の計算例をご覧ください。a＝11、b＝25とすると、cが36、dが330となります。このcとdを比べてみると、dのほうがcよりも大きい数です。他にもいろいろな数を入れて計算してみると、ほとんどの場合はdのほうがｃより大きく、cがdよりも大きくなるケースは稀なことだと分かります。皆さんも実際に計算してみてください。

この「cがdより大きくなる例は少ない」ということを予想したのが、ABC予想なのです。

つまり、ABC予想の大きなテーマは、数の「たし算的側面」の代表選手であるｃと、「かけ算的側面」の代表選手であるdを比べるということになります。一見シンプルな問題に思えますが、その解決は恐ろしく難しいのです。

大きな原因は、たし算とかけ算の関係にあります。なぜなら、「自然数において、たし算とかけ算という2つの演算は、分かちがたく結びついている」からなのです。

たし算とかけ算はどちらも小学校の算数で習うことですし、その関係は皆さんにとっても明白なことだと思います。例えば、最初に2＋2＋2＋2＝8というたし算を習ってから、2×4＝8というかけ算でも同じことが出来ると習いますよね。

たし算とかけ算は“一蓮托生”に結びついていて、望月さんはこの関係を「正則構造」と呼んでいます。その結びつきを分離したり変形したりして、勝手にいじることは出来ません。逆に言えば、正則構造に縛られているからこそ、歴史上の数学者たちが寄ってたかって挑戦しても全く歯が立たないような難問が「ABC予想」も含めていくつも存在しているというわけです。

「複数の数学」で作業する

そこで望月さんが思いついたのが、正則構造をうまく破壊し、「たし算とかけ算を分離して、別々のものとして扱う」ということでした。ですが、正則構造をいじるということは、今ある数学自体を破壊するということになってしまいます。それを避けるために、一つの数学ではなく、「複数の数学」で作業をしようと考えたのです。

ここで、理論の名称に含まれている「宇宙際」という言葉に注目します。私達は国と国の間の関係について論じる時に「国際」という言い方をしますが、望月さんの「宇宙際」という命名もこの延長線上にあります。スケールをどんどん大きくしていけば、宇宙と宇宙の間の関係について論じる時は「宇宙際」という言葉を使うことになるのです。

「宇宙」とは、我々が生き、それについて思考したり、科学したりするあらゆるモノと場所と時間など「全ての物事の一式」です。

望月さんはそれと同じように、我々が数学をする上での「数学一式」というものを考えました。それは、我々が普段の数学の様々な計算や理論を証明したりする限界であり、その「舞台」です。その数学一式の「舞台」のことを、彼は「宇宙」と呼んでいるのです。

望月さんは、数学一式ができる「舞台（宇宙）」を複数考えて、それらの間の往来や関係について論じることで、今までになかった柔軟性を生み出そうとしました。その発想にこそ、IUT理論の新しさがあります。