Qualify Marathon難問解決委員会

2022年10月1日 00:01

今回は難問の出題パターンを知って解ける問題を増やそうという記事です。※QMの出題パターン自体は別の記事でまとめています。

難問になるのはTARGETの約数が盤面数字に存在するときです。掛け算開始と掛け算終了の両方が解答として存在し得るため解くのに時間がかかります。難問のパターンを把握すると解ける問題が増えたり解答速度向上に繋がると考えています。以下では問題とともに難問のパターンを紹介します。

(A)足し引きしてからかける

[1]　盤面全体でぐるぐるさせてTARGETの約数の相手となる数字を作るパターンです。9-8+9-8×2=4のように序盤から厳しい問題が飛んでくるため注意が必要です。計算途中で負の数になるルートは排除できます。

[2]　後半でTARGETの約数が多い状況だと×を何回使うのか判別し辛い難問です。7マス解のダミー数字に惑わされると時間を食います。

[3]　TARGETがaxbの形で表せて盤面にaとbの数字があるが直接掛け算が出来ないときに複数存在する数字cを介してカーソルを移動させるパターンです。aが最初に来ると(a+c-c)xbで、aが真ん中に挟まると(c+a-c)xbの解になります。このパターン自体はそこまで難解ではありません。

[3-1]　上記の発展形としてaが直接盤面数字に出現しない場合やbとcが同じ数字になるパターンがあります。上手く見抜ければ計算自体は簡単です。

[4]　後半の掛け算が2回のパターンですが、[2]と区別できないため難度は高いです。TARGETが大きくても最初に作る数が大きいとは限りません。

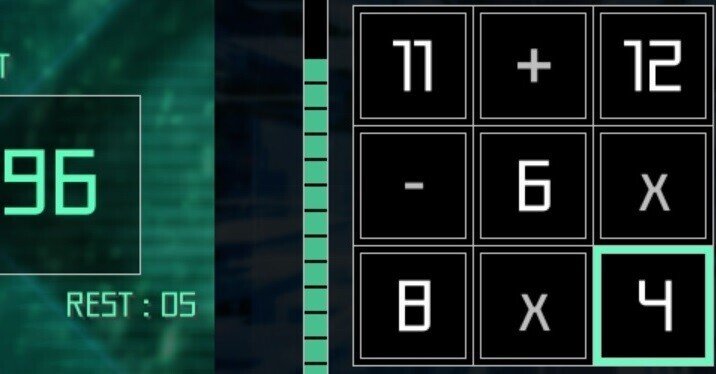
[4-1]　約数のとなる盤面の数字でaxb=cが成立していると、どちらを経由する解なのか判別するのに時間を食います。

[4-2]　足し引きが2回になって9マス解になる場合もあります。わかりやすい例だと44や66のとき11を作って×2や×3に繋ぐ形ですが、約数が増えると面倒になります。ダミー数字がないだけマシではありますが…

[4-3]　[3]のようなTARGETの約数となる盤面数字aとbがありますがaがダミー数字で他で調整してからaの値を作ってbに繋ぐケースです。辺で調整してからS字掛け算3つの形が見えにくいことも難度を上昇させています。

この基本形は「a×b±a」です。この形は変形するとa×(b±1)となり、(A)のパターンと見分けがつかないため難問となっています。

[1] a×b-c+d形　cとdの差がaになっています。表題の20がこれです。

[1-1] cとdの差がaの2倍になることもあります。分かりづらいです。

[2] a×b-c-d形　c+d=aの形です。足し算連続パターンはQMでは出ません。

[3] a×b×c±d形　よくみるあの形です。a,b,cいずれか2つの積がdです。

[3-1]　a,b,cどれかの倍数がdです。中盤でよく出現します。

[3-2]　a,b,cの約数からいくつか集めた積がdです。

[3-3]　dが12になると個人的には最悪だと思っています。

　なんか怪しいな？と思ったらS字3つ掛け算を疑うのは割と有用です。終盤は判断力が低下しがちなので84,91,98が7の倍数であることを覚えておくと役に立つかもしれません。
※こちらで使用している盤面は全て難問対策委員会本部より引用しています