
無限本の弦の平均長さは4/π
――メリークリスマス×(1週間)^-3――
こんばんは。理人です。
今回は数学をネタにしますが、大学で習うようなものではなく、高校数学を応用したみたいなものなので、高校までの数学や計算が好きな人向けです。
今回の議論では「極限」「無限大」の概念を使用します。私はε-N論法を書かなくなって久しいため、極限に関する厳密な証明はしません(できません)。なので、説明が飛び飛びだったり不完全だったりすると思いますが、「へーそんな考え方があるんだー」ぐらいに、軽い気持ちで思っててください。
学科のゼミじゃないので、鬼の首を取ったような揚げ足取りはご遠慮ください。
ちなみに、大学受験には役立ちませんので、受験生はnote見るのやめてあなたのノートの方を見て下さい。
同様に、この記事は学術論文の参考文献としても役立ちません。
この記事はCCS Advent Calendar 2024の12月7日の記事です。
前日(6日):ない!!!!
後日(8日):オワコンみたいな海底に住んでいる潜水艦(わたし)はどうすりゃいいですか?2|りょうさん
こちらの記事では難しい話をしているなあってことが分かりました。
スティールダイバーは昔ちょっとやってました。モールス信号が楽しい。
あ~^今年のアドカレの埋まらなさ、ガチでヤバいんじゃあ~^
さて、突然ですが、「1.27323954474…」という小数は何を表しているでしょうか。
ずばり、この数は $${4/π}$$ です。
「よんぶんのパイ」ではありません。「パイぶんのよん」です。
この数に関して、今回この記事では以下の主張をしたいと思います。
「単位円に無限本の弦を引くと、その長さの平均値は4/π」
単位円:半径が1の円
弦:円を構成する点のうち、任意の異なる2点を結ぶ線分
(弦の)長さ:弦の端の2点間の平面上でのユークリッド距離。単位円では最大値は2、最小値はない(無限小)とする。
ここで私は、円の中に無限に弦を引くと、その長さの平均値が
$${4/π≒1.27323954474…}$$になるという主張をしたいのです。
まずは正多角形
いきなり円を考えるのは難しいので、まずは正多角形からにします。正多角形で何かしら一般化をして、その角の数を増やしていけば(極限をとれば)いつか円になるだろうという魂胆です。
最終的に単位円になってほしいので、正多角形のなかでも特に「単位円に内接する正多角形」を考えます。
単位円に内接する正多角形のうち、任意の2頂点を結ぶ線分をここでは「対角線」と呼びます。
ここで、円に内接する正$${n}$$角形($${n}$$は自然数、$${n\geq 3}$$)に対し、「第$${l}$$対角線」($${l}$$は自然数)という言葉を以下のように定義したいと思います。
正多角形の任意の異なる2頂点A、Bをとり、頂点Aから正多角形の辺を辿って頂点Bにたどり着くまでに最少で$${l}$$本の辺を通る必要があるとき、線分ABを第$${l}$$対角線という。
難しい言い回しですが、要は「隣り合った2点を結んだ対角線は第1対角線、1点飛ばして結んだものは第2対角線、2点飛ばして結んだものは第3対角線…」もしくは「全ての対角線で、長さが短いものから第1、第2、第3…」みたいなイメージです。

「最少」なので7本(黒)はダメ。
・正三角形には第1対角線が3本しかなく、第2以降の対角線は存在しません。
・正方形には第1対角線が4本、第2対角線が2本あります。
・正五角形には第1対角線が5本、第2対角線が5本あります。
定義と例からもわかるように、第1対角線とはすなわち正多角形の辺そのものですね。辺を対角線という言葉で呼ぶことに違和感はあるでしょうが、後々のため便宜上そう呼ぶことにします。
さて、最終的には長さの平均を求めなければなりませんから、以下の2つのことを考える必要があります。
1. ある$${n}$$に対して、$${l}$$の最大値は?
2. 正$${n}$$角形の第1、第2、…第$${l}$$対角線はそれぞれ何本存在するか?
1. あるnに対して、lの最大値は?
$${l}$$の最大値、すなわち、第何対角線まで存在するのか。
$${l}$$の最大値を$${L}$$と表すことにし、$${L}$$を$${n}$$の関数として表す方法を考えます。
$${n}$$が偶数と奇数で状況が違うので、場合分けして考えます。
・$${n}$$が偶数の場合
第$${L}$$対角線、すなわち対角線の中で最長のものは、ある点からちょうど反対側にある点です。座標平面で$${(1,0)}$$のところに第$${L}$$対角線の一方の端点Aを置いたとすると、もう一方の端点Bは$${(-1,0)}$$にあるイメージです。このとき、頂点A、B以外の点はいくつあるかというと当然$${n-2}$$個です。それが座標平面の$${y>0}$$側と$${y<0}$$側に半分ずつ配置されているはずなので、頂点Aから頂点Bへたどり着くまでに通る点はA、B以外には$${(n-2)/2=n/2-1}$$個あります。よって、頂点Aから頂点Bへたどり着くまでに通る辺の数はそれより1多いはず(植木算)なので、$${L=n/2}$$です。
・$${n}$$が奇数の場合
偶数の場合を応用して考えてみます。$${n}$$が偶数の場合の最長の対角線(第$${L}$$対角線)の次に長い対角線(第$${(L-1)}$$対角線)を考えてみます。$${(1,0)}$$が第$${(L-1)}$$対角線の一方の端であるとき、もう一方は$${(-1,0)}$$の隣の点($${(-1,0)}$$から辺を1本だけ辿って辿り着く点)であるはずです。さてこの状況で、$${(-1,0)}$$の点をなかったことにして、$${n}$$を奇数にしてみると、さっきまで$${n}$$が偶数の正$${n}$$角形の第$${(L-1)}$$対角線だった対角線が、$${n}$$が奇数の正$${n}$$角形における最長の対角線になってますね。つまり、$${n}$$が奇数の正$${n}$$角形の$${L}$$は、偶数の場合の$${n}$$から単に1小さくして求めればよいと言えます。
よって、$${n}$$が奇数の場合、$${L=(n-1)/2}$$です。
2. 正n角形の第1、第2…第l対角線はそれぞれ何本存在するか?
$${n}$$が偶数の場合、第$${L}$$対角線以外は、ある頂点を基準としてそこから$${l}$$本の辺を辿った先の頂点と線分を作り、それが全ての頂点を基準に異なる線分を形成できるため本数は$${n}$$になります。一方、第$${L}$$対角線(第$${n/2}$$対角線)はある頂点を基準としてちょうど反対側の頂点と結ばれた線分であり、その反対側の頂点を基準とした場合は同一の線分になるので数えません。よって本数は$${n/2}$$になります。
$${n}$$が奇数の場合、どの対角線も、ある頂点を基準としてそこから$${l}$$本の辺を辿った先の頂点と線分を作り、それが全ての頂点を基準に異なる線分を形成できるため本数は$${n}$$になります。
これらの結果を数式上で扱うために、以下の関数$${f(n,l)}$$を導入します。この関数は、自然数$${n,l}$$の関数で、正$${n}$$角形の第$${l}$$対角線の本数を表します。一見そうは見えないとは思いますが、実際に$${n,l}$$に色々と代入すると、上記の長い説明をこの関数1つで表していると分かると思います。
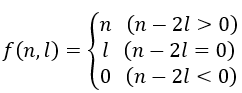
別の関数で変形して場合分けをなくすこともできますが、今回は必要ないのでこのまま進めます。
辺の長さの平均は?
ここまで長々と導入してきましたが、実際に辺の長さと平均値を出していきます。
辺の長さを出すと言えば余弦定理ですね。シンプルな高校数学です。
第$${l}$$対角線の端点をA、Bとし、単位円の中心をOとするとき、三角形OABに対して余弦定理を用いると、ABの長さ=第$${l}$$対角線の長さは
$${\sqrt{2-2\cos{2πl \over n}}}$$
となります。
図を書けばすぐ分かりますが一応導出しておきます。
単位円に内接する正$${n}$$角形を考え、単位円の中心と各頂点を線で結んだとき、合同な二等辺三角形が$${n}$$個できます。そしてその頂角は、$${360°=2π}$$を$${n}$$等分なので$${2π/n}$$と表せます。
ここで三角形OABに対して余弦定理を適用し、線分AB(第$${l}$$対角線)の長さを考えると、三角形OABは$${OA=OB=1}$$の二等辺三角形で、その頂角は$${2π/n}$$が$${l}$$個分なので$${2πl/n}$$です。よって線分ABの長さは上式のように求まるわけです。
ここで、$${n}$$が偶数のときの第$${L}$$対角線では三角形OABができないことになってしまいますが、その場合は$${L=n/2}$$なので、
$${\sqrt{2-2\cos{2πL \over n}}=\sqrt{2-2\cos{π}}=\sqrt{2+2}=\sqrt{4}=2}$$
となります。$${n}$$が偶数のとき、第$${L}$$対角線は単位円の直径と同じなので長さは明らかに2です。つまり、上記の数式はそのような場合も包含しているといえるので一旦OKとします。
第$${l}$$対角線の本数と長さが出たので、これらを掛け算すると、ある$${l}$$について「第$${l}$$対角線」の長さの合計が出ます。
$${f(n,l)\sqrt{2-2\cos{2πl \over n}}}$$
これを第1対角線から第$${L}$$対角線まで足し合わせることにより、「正$${n}$$角形にある全ての対角線の長さの和」が出ることになります。
$${\sum_{l=1}^L f(n,l)\sqrt{2-2\cos{2πl \over n}}}$$
一方、正$${n}$$角形に対角線が合計で何本あるかは、第$${l}$$対角線の本数の$${l=1}$$から$${L}$$までの和なので
$${\sum_{l=1}^L f(n,l)}$$
…と表してもいいのですが、対角線(辺を含む)を引くには、単純に異なる頂点2つを選べばいいので、これは$${n}$$個のものから2つを選ぶ場合の数として考えることができるため
$${\sum_{l=1}^L f(n,l)={n(n-1)\over 2}}$$
と、簡単にすることができます。
さて、今求めようとしているのは長さの平均値なので、長さの和を本数で割ります。これを、正$${n}$$角形に対する対角線平均長と呼ぶことにし、記号は$${A(n)}$$と書くことにします。
$${A(n)={{2\over n(n-1)}\sum_{l=1}^L f(n,l)\sqrt{2-2\cos{2πl \over n}}}}$$
$${n\geq3}$$なので、分母は0になりません。
関数fを簡単にする
対角線平均長が式化できましたが、やはり$${f(n,l)}$$が厄介なので、もう少し簡略化します。
まず、$${n\geq4}$$として、和を$${1 \leq l \leq L-1}$$と$${l=L}$$に分けて考えます。
$${\sum_{l=1}^L f(n,l)\sqrt{2-2\cos{2πl \over n}}}$$
$${=\sum_{l=1}^{L-1} f(n,l)\sqrt{2-2\cos{2πl \over n}}+f(n,L)\sqrt{2-2\cos{2πL \over n}}}$$
$${1 \leq l \leq L-1}$$のとき、$${n}$$の偶奇にかかわらず$${f(n,l)=n}$$になります(代入すれば明らか)。
一方で$${l=L}$$のとき、$${n}$$が偶数なら$${f(n,L)=n/2}$$、奇数なら$${f(n,L)=n}$$でしたから、ここで以下のように$${f(n,L)}$$を変形できます。
$${f(n,L)={{3-(-1)^n}\over 4}n}$$
唐突に見えますが、単純に$${n}$$が偶数のとき$${(-1)^n}$$は1、$${n}$$が奇数のとき$${(-1)^n}$$は-1になることに注目したものなので、式が表していることは見た目よりシンプルです。
以上より対角線平均長の和の部分は
$${\sum_{l=1}^L f(n,l)\sqrt{2-2\cos{2πl \over n}}}$$
$${=\sum_{l=1}^{L-1} f(n,l)\sqrt{2-2\cos{2πl \over n}}+f(n,L)\sqrt{2-2\cos{2πL \over n}}}$$
$${=\sum_{l=1}^{L-1} n\sqrt{2-2\cos{2πl \over n}}+{{3-(-1)^n}\over 4}n\sqrt{2-2\cos{2πL \over n}}}$$
$${=n(\sum_{l=1}^{L-1} \sqrt{2-2\cos{2πl \over n}}+{{3-(-1)^n}\over 4}\sqrt{2-2\cos{2πL \over n}})}$$
対角線平均長の一般式を求める
以上より、対角線平均長$${A(n)}$$は
$${A(n)={{2\over n(n-1)}×n(\sum_{l=1}^{L-1} \sqrt{2-2\cos{2πl \over n}}+{{3-(-1)^n}\over 4}\sqrt{2-2\cos{2πL \over n}})}}$$
$${={{2\over n-1}×(\sum_{l=1}^{L-1} \sqrt{2-2\cos{2πl \over n}}+{{3-(-1)^n}\over 4}\sqrt{2-2\cos{2πL \over n}})}}$$
$${={2\over n-1}\sum_{l=1}^{L-1} \sqrt{2-2\cos{2πl \over n}}+{{3-(-1)^n}\over 2(n-1)}\sqrt{2-2\cos{2πL \over n}}}$$
ここまで$${n\geq4}$$としてきましたが、これは総和がバグらないように$${L-1\geq1}$$にしたかったためです。つまり、正三角形、すなわち$${n=3}$$のときは上記の分解した式ではなく、変形前の式を使いましょう。
$${A(3)={{2\over 3(3-1)}\sum_{l=1}^1 f(3,l)\sqrt{2-2\cos{2πl \over3}}}}$$
$${={1\over3}f(3,1)\sqrt{2-2\cos{{2\over3}π}}={1\over3}×3\sqrt{2+1}=\sqrt3}$$
円で考える
ここから極限が出てくるため、説明がさらにあやふやになります。本職の数学者の方は体調に悪影響を及ぼす可能性があるため、ここで閲覧をやめるか、体調を崩してでも読む覚悟を今のうちに決めて下さい。
極限を求めたいのですが、「極限をとる操作の線形性」をどうしても使いたいところです。
$${f(x)\to \alpha, g(x)\to \beta \Rightarrow f(x)+g(x)\to \alpha + \beta}$$
みたいなやつです。
本来は、それぞれの関数の極限が一定の値に収束することを示す必要がありますが、ここを省略したいと思います。
各項が上と下に有界なことはいうて簡単に示せるんですが、それぞれが収束するか振動するかをきっちり証明するのが嫌になりました。
ということで、$${A(n)}$$の$${n\to \infty}$$での極限を以下のように変形します。
$${\lim_{n\to \infty}A(n)}$$
$${=\lim_{n\to \infty}{2\over n-1}\sum_{l=1}^{L-1} \sqrt{2-2\cos{2πl \over n}}+\lim_{n\to \infty}{{3-(-1)^n}\over 2(n-1)}\sqrt{2-2\cos{2πL \over n}}}$$
まず簡単な方の第2項に注目します。
第$${L}$$対角線の長さを大雑把に上と下から評価します。対角線の長さは0より大きく2以下であるということだったので、
$${0<\sqrt{2-2\cos{2πL \over n}}\leq2}$$
$${{3-(-1)^n}\over 2(n-1)}$$は$${n\geq4}$$で明らかに0以上なので辺々$${{3-(-1)^n}\over 2(n-1)}$$をかけて
$${0\leq{{3-(-1)^n}\over 2(n-1)}\sqrt{2-2\cos{2πL \over n}}\leq{{3-(-1)^n}\over n-1}\leq{4\over{n-1}}}$$
ここで、最右辺は$${n\to \infty}$$で0に収束するので、挟みうちの原理により
$${{\lim_{n\to \infty}}{{3-(-1)^n}\over 2(n-1)}\sqrt{2-2\cos{2πL \over n}}=0}$$
一方、和の記号を含む方の第1項は無理やり区分求積に変形します。
$${\lim_{n\to \infty}{2\over n-1}\sum_{l=1}^{L-1} \sqrt{2-2\cos{2πl \over n}}=\lim_{n\to \infty}{1\over n}\sum_{l=1}^{n}\sqrt{2-2\cos{2πl \over n}}=\int_{0}^{1}\sqrt{2-2\cos{2πx}}dx}$$
最後にして最大のあやふやポイントです。ここでの近似は、結論が都合よく導き出せるようにやっている節があるので、そういう意味では「ベルトランのパラドックス」に似ているところがあります。こういうのをすっきり議論できる人が数学者なんだろうなあ。
積分にできることが認められればあとは単純です。
$${\int_{0}^{1}\sqrt{2-2\cos{2πx}}dx=\sqrt2 \int_{0}^{1}\sqrt{1-\cos2πx}dx}$$
$${2πx=y}$$と置換して
$${\sqrt2 \int_{0}^{1}\sqrt{1-\cos2πx}dx={\sqrt2\over2π}\int_{0}^{2π}\sqrt{1-\cos y}dy={\sqrt2\over2π}\int_{0}^{2π}\sqrt{2\sin^2{y\over2}}dy={1\overπ}\int_{0}^{2π}|\sin{y\over2}|dy={1\overπ}\int_{0}^{2π}\sin{y\over2}dy={1\overπ}[-2\cos{y\over2}]_{0}^{2π}={-2\overπ}(\cosπ-\cos0)=4/π}$$
ということで、めでたく(?)
$${\lim_{n\to \infty}A(n)=4/π}$$
に、なったんじゃないかと思います。
実際に計算してみる
なぜこんなに怪しい、あやふやな議論をしてまで$${4/π}$$に執着しているのか、ということですが、これは実際に計算してみるとその値になりそうな予測が立っているからです。
純粋な数学にはあるまじき帰納的な結論ですが、以下に実例を並べてみます。収束は非常に遅いですが、なんとなく$${4/π=1.27323954474…}$$に近づいている気がしませんか?
$${A(4)={2\over{4-1}}({\sum_{l=1}^{1}}\sqrt{2-2\cos{2πl\over4}}+{1\over2}{\sqrt{2-2\cos{2π×2\over4}}})≒1.60948…}$$
$${A(16)={2\over 16-1}({\sum_{l=1}^{7}}\sqrt{2-2\cos{2πl\over 16}}+{1\over2}{\sqrt{2-2\cos{2π×8\over 16}}})=1.35376…}$$
$${A(256)={2\over 256-1}({\sum_{l=1}^{127}}\sqrt{2-2\cos{2πl\over 256}}+{1\over2}{\sqrt{2-2\cos{2π×128\over 256}}})=1.27822…}$$
$${A(65536)={2\over 65536-1}({\sum_{l=1}^{32767}}\sqrt{2-2\cos{2πl\over 65536}}+{1\over2}{\sqrt{2-2\cos{2π×32768\over 65536}}})=1.27325…}$$
(これ以上$${n}$$を大きくしたらWolframAlpha君が爆発しました。)
あとがき
ということで、12月7日の記事だということで、$${4/π=1.27…}$$に関する記事をあげました(1月27日なんて知らん)。
この辺境の地に埋もれた記事を見て文句をつけてくる数学者が現れる可能性を考えると夜も眠れません。でも私は最初に言いましたからね。あくまでそういう考え方もあるんだねぇ、程度に考えて、揚げ足取りはご遠慮くださいってね。
揚げ足取りするならコメント欄じゃなくてあなたの論文に書きましょう。
ということで、お疲れ様でした。今年のクリスマスケーキはホールケーキを買って、ぜひ無限本の弦でカットして食べて下さい。
またこんど!
――アドカレ埋まるんか?――
