度数分布表から偏差値を求める #1

株式会社リュディアです。個人の成績は既知で全体の度数分布表が与えられたときに偏差値を求める方法についてまとめます。

学校から子供のテストの点数と平均点は教えてもらえるけど偏差値がわからればよいな、と思っている方は多いのでは？その際に度数分布表やヒストグラムが提供されるのであれば自分で計算することが可能です。平均点に対して良い点か悪い点かという議論は分散や標準偏差を考えないと意味がない、という話は何度もしてきました。そこで今回は度数分布表と平均点から自分で偏差値を求める方法についてまとめてみます。

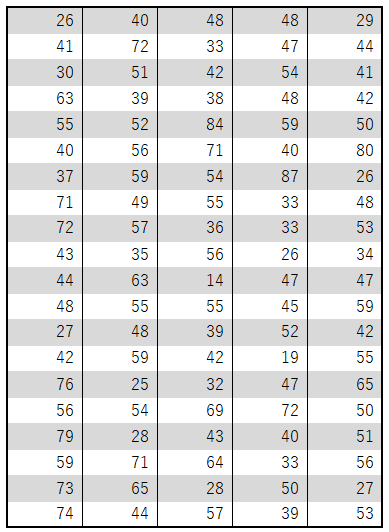
乱数を使って以下のようなデータを生成しました。100人のテストの点数で算術平均は 49.1 です。

たとえば太郎が100点満点のテストで 58点をとりました。先生が平均は 49.1 点だと教えてくれました。また学校から度数分布表が配布されました。例えば以下のようなものです。よくある光景だと思います。また受験者数は100人とします。

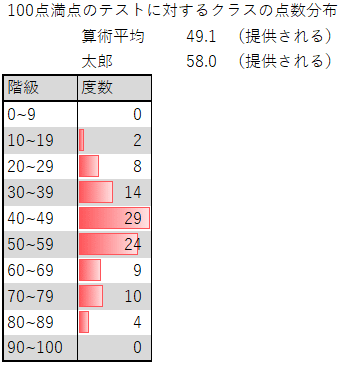
今回は太郎の偏差値を求めるためだけの操作方法をまとめます。上記のような度数分布表を紙で配布されたらエクセルに入力するところまで頑張ってください。入力が終わったら以下のように表を補ってください。以下、補ってもらいたい項目についての説明です。項目の意味は別途まとめますので計算方法のみです。

階級値

階級の下限と上限の数字を加えて2 で割ります。階級を代表する点として真ん中の点を決めます。

相対度数

各階級の度数、つまり人数の合計人数に対する比率です。今回であれば各階級の度数を 受験者の合計100 で割った数字です。

累積相対度数

相対度数を順に加えていきます。今回のまとめでは使いませんが次回以降で利用します。今回は累積相対度数が最終的に 1.0 になることを確認しエクセルの数式にミスがないか確認するために使ってください。

偏差（階級値 - 平均値）

各階級の偏差を求めます。偏差とは平均からのずれです。各階級の階級値から平均値を引いた数です。ここでは平均は 49.1 点ですので各階級の階級値から 49.1 を引いた数を記載します。

偏差の2乗 x 相対度数

各階級で既に求まっている偏差の2乗 x 相対度数を求めます。

ここまで準備ができたら後は簡単です。各階級の偏差の2乗 x 相対度数を求め全階級に対して加算します。これが分散になります。ここでは 251 です。分散のルートが標準偏差でしたので標準偏差 σ は 16 となります。偏差値を求める式は以下です。

太郎の点数 58、クラスの平均点 49.1、標準偏差 16 がわかったので太郎の偏差値は 56 となります。

偏差値については以下の記事でもまとめていますので参考にしてください。

今回は度数分布表から偏差値を求める方法のみを記載しました。なぜこの計算で求まるのかは次回にまとめます。まずはこの方法で学校から配布されたプリントを使って自分の偏差値を計算してみてください。

続きはこちらからどうぞ。

では、ごきげんよう。