ローレンツ曲線とジニ係数 #3
引き続きローレンツ曲線とジニ係数についてまとめてみたいと思います。前2回の記事の続きですので先に以下の2つの記事を読んでください。
ジニ係数の計算方法は前回に説明しましたがローレンツ曲線の積分をどうするか、という問題にあたりました。今回はこの部分を具体的に扱う方法について記載します。
次の図をみてください。今、求めたいのはローレンツ曲線の下部とX軸で囲まれた部分の面積です。

求めたい部分を計算するための積分の式もつけておきます。
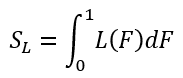
図中の緑の台形部分を見てください。この台形の面積をすべて加算すると積分の結果にほぼ等しくなることはわかりますよね。つまり以下の近似計算により積分計算を行えるということです。
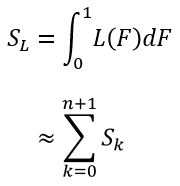
ローレンツ曲線とジニ係数 #1 の具体的な問題に戻ってみたいと思います。ローレンツ曲線に台形を追記すると以下のようになります。

この段階の面積を求め、さらに台形の合計値、ジニ係数まで求めたのが以下の表です。
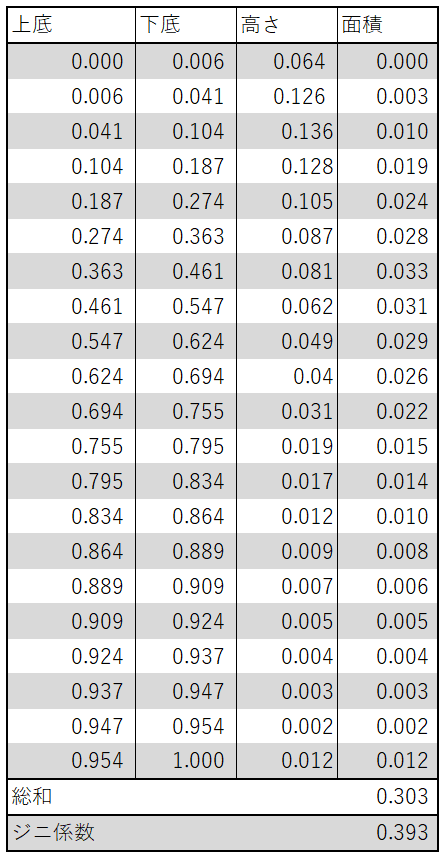
ジニ係数は 0.393 となりました。実際、以下の厚労省が報告しているジニ係数 0.37 よりは大きいですが的外れな値でもないので勉強の課題としてご容赦願いたいと思います。
今回は具体的にジニ係数を求めてみました。前2回を含め全3回に渡ってローレンツ曲線、ジニ係数の意味、具体的な計算と進めてきました。メディアでよく目にするジニ係数ですが、実際に自分で計算してみると意味が理解できた感じがしてきます。
Wikipedia によると社会騒乱多発の警戒ラインは0.4であると記載されています。0.4 に対して今回の計算では 0.39 でありかなり近づいていることがわかります。日本も富の隔たりが大きくなっていると考えるのか、ぎりぎりのところで抑えられている、と考えるのか難しいとことろではないでしょうか。
では、ごきげんよう。
