G検定 / 統計検定 確率分布 #3

株式会社リュディアです。引き続き確率分布についてまとめていきます。

前回までの確率分布についてのまとめへのリンクは以下を参考にしてください。

今回は具体例としてベルヌーイ分布についてまとめてみます。一言で説明すると結果が二択になるような試行をベルヌーイ試行と言い、ベルヌーイ試行が従う確率分布をベルヌーイ分布と言います。例えばコイントスで表裏いずれが出るかはベルヌーイ試行の代表例です。二択と言われると限定されるような気がしますが「はい」か「いいえ」で回答できる試行と考えればどうでしょうか？

サイコロを振った出目が偶数かどうか

昼食で食べるおにぎりの具は梅かどうか

住民投票で有権者をランダムに抽出して、その有権者が住民投票で「はい」と投票するかどうか

これらの例もすべてベルヌーイ試行であり確率分布はベルヌーイ分布に従います。ではベルヌーイ分布の確率質量関数を考えます。ベルヌーイ分布は離散分布の一つなので確率質量関数を考える必要がありますね。コイントスを具体例として考えます。コイントスでコインが表になる事象を X = 1、裏になる事象を X = 0 とするとそれぞれの確率を以下のように表現できます。

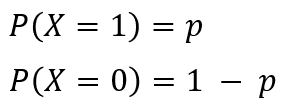
表が出る確率 P( X = 1 ) を p とすると裏が出る確率 P( X = 0 ) は 1 - p になりますね。これらをまとめて 1 つの式で表現した確率質量関数は以下のようになります。ただし k = 0 または 1 です。

コイントスで考えると p = 1/2 、つまりコインの表裏のいずれが出現するかは等確率になります。具体的に見てみましょう。

f(k = 1) = P ( X = 1 ) = 1/2

f(k = 0) = P ( X = 0 ) = 1/2

コイントスでは表裏いずれかが出る確率は 1/2 であることがわかりますね。

最後にベルヌーイ分布の平均と分散を以下に示しておきます。

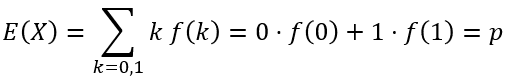
コイントスのように p = 1/2 だとすると平均 E(X) = 1/2、分散 V(X) = 1/4 になります。ベルヌーイ分布は最も単純な離散分布です。

G検定 / 統計検定 確率分布に関するまとめの続きは以下からどうぞ。

では、ごきげんよう。