G検定 ニューラルネットワークと活性化関数 #3
株式会社リュディアです。G検定対策として G検定 ニューラルネットワーク #2 に続き活性化関数についてまとめていきたいと思います。
G検定 ニューラルネットワーク #2 では活性化関数としてステップ関数についてまとめました。ステップ関数は出力が 1 または 0 になる関数なので、もしすべてのニューロンにステップ関数を適用するとニューラルネットワーク全体の出力として 1 または 0、つまり入力に対して Yes or No の判断しかできなくなります。現実の問題に適用したニューラルネットワークで Yes or No の結論を得るよりも、A である確率 70%、Bである確率 20%、Cである確率 10% という確率の方が有意な場合が多いのでは?ということは容易に想像できますよね。
今回はステップ関数の代わりにシグモイド関数を使って、出現確率を得る方法についてまとめていきたいと思います。シグモイド関数とはどのようなものでしょうか?以下の図をみてください。シグモイド関数の数式とグラフを記載しています。横軸があるニューロンへの入力としたとき、ニューロンへの入力に依存して縦軸が 0 ~ 1 の値、つまりYes or No ではなく確率が得られることになります。0.7 であれば 70% の確率ということです。
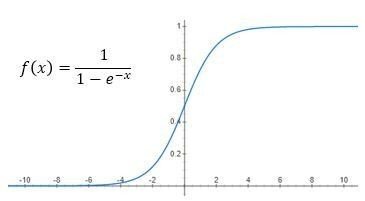
ステップ関数ではなくシグモイド関数を用いることでどのような旨味があるのでしょうか?
1. Yes or No ではなく、ある条件が妥当である確率を計算可能、G検定公式テキストの用語を使うなら分類だけではなくクラスタリングにも適用可能
2. ステップ関数は微分不可能であるがシグモイド関数は微分可能、これは数理モデルとしてニューラルネットワークを扱う際に便利(深い意味は考えないで、理論屋さんにとって楽という程度で問題ないです)
次に G検定公式テキスト p138 で説明されている tanh 関数について見てみましょう。まず以下の数式を見てください。
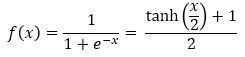
実はシグモイド関数は tanh を使った式に変形できます。これは何を意味しているのでしょうか?さらに詳しく見るためにシグモイド関数と tanh(x) のグラフを重ねて描画してみました。緑がシグモイド関数で赤が tanh(x) のグラフです。
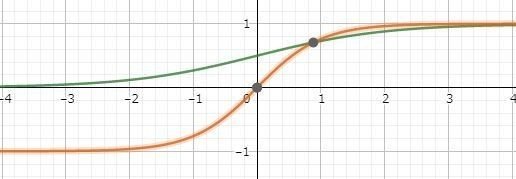
緑のシグモイド関数は f(x) の値の範囲が 0~ 1であるのに対し f(x) = tanh(x) は -1~ 1 となります。従来から tanh(x) が使われていた背景としては活性化関数は原点を通過すべき、という考え方があったためと言われています。
私見ですが活性化関数は何でもいい、ただし過去の膨大な研究成果から、どの関数がよさそう、という経験則は存在している、と理解しています。逆誤差伝搬法でうまく逆伝搬しない、という理論的な背景があることはわかります。しかし基本はどのような入力に対しても決まった範囲の値を返すような関数が活性化関数であり、流行りすたれがあるものだと思っています。
では、ごきげんよう。
