代表値といろいろな平均

株式会社リュディアです。今回は具体的なG検定対策ではないですが、代表値といろいろな平均についてまとめてみたいと思います。データサイエンスや統計学は機械学習の勉強をする上で非常に重要な分野です。基本的な用語はしっかりと身につけておいてください。

最初に代表値と平均値についてまとめます。あるデータの集まりに対して代表値を考えることがあります。日常生活では平均値を考えることが多いのですが代表値には平均値、中央値、最頻値の 3つがあります。平均値については後でまとめますので、中央値と最頻値について先にまとめます。

中央値はデータを大きさの順に並べて中央に来るデータのことです。

最頻値は最も頻度が高いデータのことです。ヒストグラムを作ったときに出現回数が最も多いデータでもあります。

では平均値について算術平均、幾何平均、調和平均の 3 つについてまとめます。

算術平均

一般的に平均値と言った場合には算術平均（arithmetic mean）のことをさします。相加平均とも呼びます。2 つの数 a1, a2 の算術平均は以下の数式で計算します。皆さんも普段使いますよね？

2 つ以上の n 個の数の算術平均を求める場合は以下の計算式になります。すべての数の和をとって n で割ります。

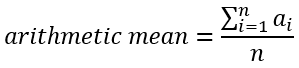
幾何平均

相乗平均とも言います。2 つの数 a1, a2 の幾何平均は以下の数式で計算します。2つの数の積をとって平方根をとります。

2 つ以上の n 個の数の幾何平均を求める場合は以下の計算式になります。すべての数の積をとって n 乗根をとります。

調和平均

2 つの数 a1, a2 の調和平均は以下の数式で計算します。2つの数の逆数の算術平均の逆数をとります。

2 つの数ではなく n 個の数の調和平均を求める場合は以下の計算式になります。すべての数の逆数の算術平均の逆数となります。

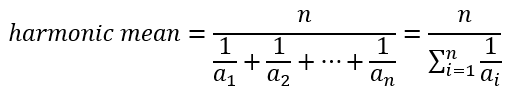
幾何平均の用途

算術平均は日常的に使うので用途をイメージしやすいと思うのですが幾何平均はどのようなときに使うのでしょうか？具体例をあげてみてみましょう。

皆さんが株や投資信託のような投資商品を購入したとします。投資商品は年間の運用実績を公開します。たとえば前年と比較して 15% の実績で資産が変動した、あるいは -10%の実績で資産が変動した、という情報です。仮に以下のような運用実績の投資商品があるとします。元本は100円であるとします。2020年の結果は +15% で運用額は 115万円に増加しました。2021年は 2020年に対して +5.2% で運用額は 120.98万円に増加しました。このように5年間の運用実績が公開された場合の平均を考えてみましょう。

計算すると運用実績の算術平均は 3.24%、幾何平均は 2.82% となります。では次に元本に対して年率を算術平均である 3.24%、幾何平均 2.82% で5年間運用した場合を計算してみます。

幾何平均を使った計算値は元の表と一致していますが算術平均を使った計算値では値がずれています。考えてみたら当たりまえなのですが、運用実績は前年に対するパーセンテージであって、元本に対するパーセンテージではありません。毎年基準が変わっていることに注意する必要があります。このような場合は算術平均は意味をなさず幾何平均を使うべきです。

変動金利の住宅ローン残金の計算、企業の決算の売上高や利益の増加率を扱う場合は幾何平均を使うべきです。

調和平均の用途

有名な用途は以下の問題です。小学校、中学校の算数で出てきます。

Aさんは家から2km 先のスーパーまで買い物にいきます。行くときは時速 5km/時でしたが、帰るときは時速 2km/時でした。平均の速度を求めなさい。

算術平均を使って ( 5 + 2 ) / 2 = 3.5 km/時と考えた方は間違いです。実際に計算してみましょう。

行くときにかかった時間は 2 / 5 = 0.4 時間です。帰るときにかかった時間は 2 / 2 = 1時間です。往復で 2 + 2 = 4km の距離に 0.4 + 1 = 1.4 時間かかっています。往復の総距離に対する平均速度は 4 / 1.4 = 2.857 km/時であり算術平均で求めた 3.5km/時 とは異なります。では調和平均で求めてみましょう。2 / (1/2 + 1/5) = 2.857 km/時となり一致します。

他に電気回路分野の並列接続の合成抵抗でも調和平均を使います。確率の平均を計算する際にも調和平均を使います。

今回は代表値と平均値についてまとめてみました。統計学やデータサイエンスにおける重要な考え方ですのでしっかりと理解してください。

では、ごきげんよう。