G検定 / 統計検定 確率分布 #7

株式会社リュディアです。引き続き確率分布についてまとめていきます。

前回までの確率分布についてのまとめへのリンクは以下を参考にしてください。

今回は最も有名な確率分布と言ってもよい正規分布についてまとめてみます。ガウス分布とも呼ばれます。

多くの確率変数が正規分布に従い、また分布という言葉に対して皆さんの頭の中にも正規分布のグラフが浮かんでいるのではないでしょうか？実際、多数のデータの分布が正規分布に従うことがわかっています。

まず正規分布を具体的にイメージしてもらうために確率密度関数から見ていきましょう。分布の平均をμ、分散をσの2乗とすると、正規分布の確率密度関数は以下のようになります。

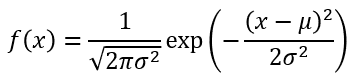
細かい話ですが x は実数であり連続分布です。つまり以下のように定義されます。

また正規分布を表現する記号として以下を用います。

このことからもわかるように正規表現は平均と分散のみで規定される分布と言えます。また特に N(0, 1) のことを標準正規分布と呼び確率密度関数は以下のようになります。

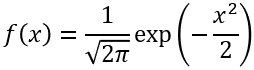
確率密度関数のグラフを見て平均と分散が変化したときに正規分布の曲線がどのように変化するか見てみましょう。

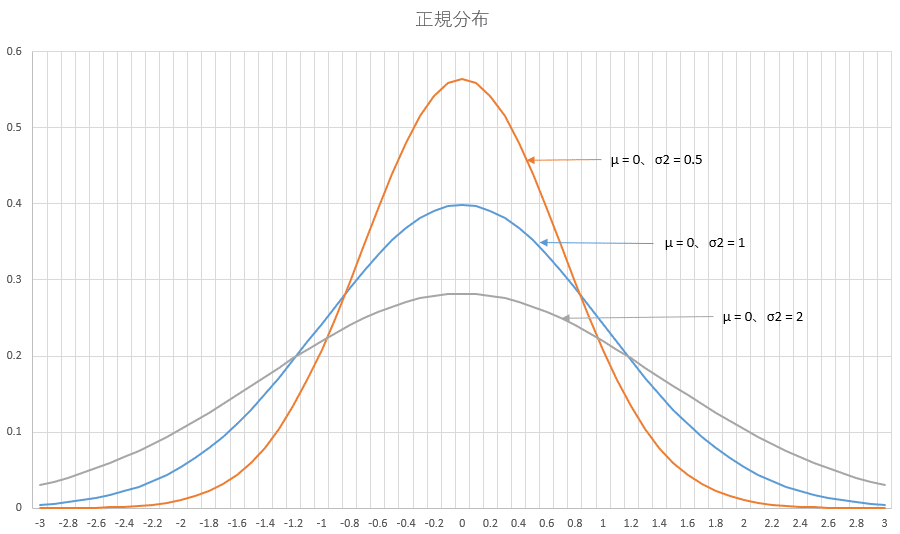
分散が小さくなると中央部への集中度合いが強い、つまり縦軸方向に尖ったグラフになり、分散が大きくなると横方向に広がった形状になります。分散自体がデータの拡がり具合を表現するものなので感覚とも合致しますね。

また平均値を中心として左右対称であることも容易に理解できると思います。さらに3つの代表値、つまり平均、中央値、最頻値が一致していることもわかりますね。代表値について過去にまとめていますので詳細を知りたい方は以下の記事を参考にしてください。

正規分布では特に標準偏差σを用いてデータの分布を表現します。以下の図を見てください。標準正規分布、つまり平均 μ = 0、分散σ2 = 1 のグラフです。平均を中心として左右に±σ、±2σ、±3σの範囲のデータが全データのうちどれくらいを占めるか正規分布では決まっています。±σの範囲に68%のデータが含まれ、±2σの範囲に 95%のデータが含まれ、±3σの範囲には99.7% のデータが含まれます。

この性質を使ってテストの偏差値は計算されています。今回は正規分布についてまとめました。性質も含めてしっかりと理解してください。

G検定 / 統計検定 確率分布に関するまとめの続きは以下からどうぞ。

では、ごきげんよう。