G検定 / 統計検定 データの集計 #2
株式会社リュディアです。前回に引き続きデータの集計についてまとめていきます。
前回までのG検定 / 統計検定 データの集計のまとめへのリンクは以下を参考にしてください。
今回はばらつきの指標についてです。前回はデータの中心がどこにあるか?という議論でしたが今回はデータ全体が中心からどれくらいばらついているか?という指標についてまとめてみます。四分位範囲、平均絶対偏差、分散、標準偏差の4つについてまとめてみます。
最初は四分位(しぶんい)範囲についてです。まず一言で書くとデータの中央 50% が分布している範囲のことです。ある数値データが与えられたとします。そのデータを小さい数から大きい数になるように並べました。そのとき中央にある数を第2四分位数と呼びます。データが偶数個の場合は中央のデータが2つ存在しますので2つのデータの平均値を第2四分位数とします。
第2四分位数が決まると第2四分位数を基準としデータを前半、後半の2つにわけることが可能です。前半をさらに 2 つにわけたとき中央にある数を第1四分位数と呼びます。後半を2つにわけたとき中央にある数を第3四分位数と呼びます。つまりそれぞれの四分位数は以下のようになります。
第1四分位数:下位 25% までの数を含む上限となる数
第2四分位数:下位 50% までの数を含む上限となる数
第3四分位数:下位 75% までの数を含む上限となる数
図で見ると以下のようなイメージになります。
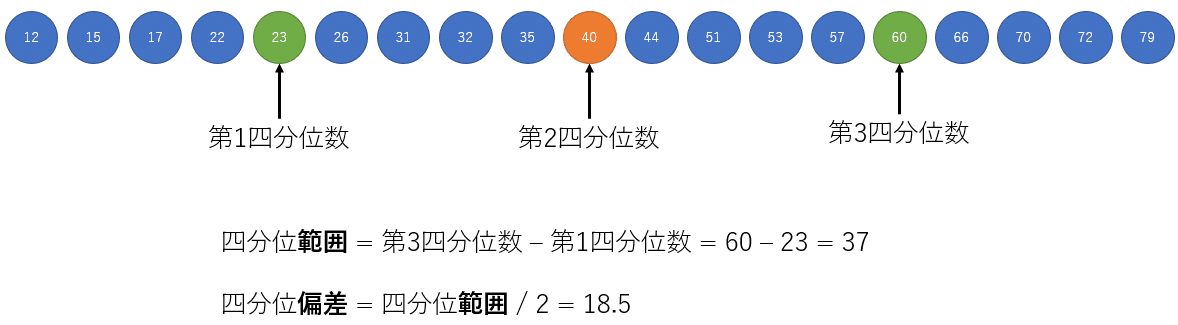
次に本題のばらつきの指標である四分位範囲です。四分位範囲は第3四分位数と第1四分位数の差です。つまりデータの中央半分がどの範囲に分布しているかを示す指標です。
ついでではありますが四分位偏差は四分位範囲を2で割ったものです。ただ私は実際のデータ解析で四分位偏差を使ってるのを見たことがないので紹介だけにしておきます。
最後にパーセンタイルという用語を紹介しておきます。例えば第1四分位数は 25パーセンタイル値とも言います。値 x が 25パーセンタイル値であるとは x よりも小さな値のデータ数が全データの 25% あることを示します。つまり四分位数は次のように言い換えることができます。
第1四分位数 = 25 パーセンタイル値
第2四分位数 = 50 パーセンタイル値
第3四分位数 = 75 パーセンタイル値
今回は四分位数、四分位範囲を中心にデータのばらつきについてまとめました。
G検定 / 統計検定 データの集計に関するまとめの続きは以下からどうぞ。
では、ごきげんよう。
