G検定 標準化、正規化、正則化
株式会社リュディアです。今日は標準化、正規化、正則化についてまとめてみます。初めてG検定公式テキストで見た方はどれもよく似た雰囲気に感じるのでしっかりと区別できるようになってください。
まず大きく「標準化、正規化」と正則化は根本的に異なることを意識してください。
標準化、正規化:データの前処理で使う考え方でデータの加工方法によって標準化、正規化という名称になっている。
正則化:過学習を抑制するための手法
まず正則化から済ませてしまいましょう。過学習を起こす、ということは特定のデータに対して過度に重みが調整されてしまうということです。そこで重みの取りうる範囲を制限してみてはどうか?というのが正則化の考え方です。G検定では以下の 2つの正則化技術が問われます。
L1 正則化:一部のパラメータをゼロにすることで正則化処理を行います。この方法を回帰に適用したものをラッソ回帰と呼びます。
L2 正則化:パラメータの大きさにあわせてパラメータをゼロに近づけることで正則化処理を行います。この方法を回帰に適用したものをリッジ回帰と呼びます。
ここで少し横道にそれますがラッソ回帰とリッジ回帰の双方を適用した手法をElastic Net と呼ぶことも知っておいてください。
次に標準化と正規化です。それぞれを文章で記載すると以下のようになります。
標準化:元データを平均が 0、標準偏差が 1 になるように変換する処理
正規化:元データを最小値が 0、最大値が 1 になるように変換する処理
元々は次元の違う複数のデータの範囲を揃えるための考え方です。たとえば体重の分布と視力の分布を使って機械学習することを考えます。体重は40kg ~ 70kg、視力は 0.1 ~ 1.5程度で、これらの数字を直接比較や演算すると意味がないことはわかりますよね。体重も視力も特定の範囲の値にスケーリングする方法が標準化、正規化です。
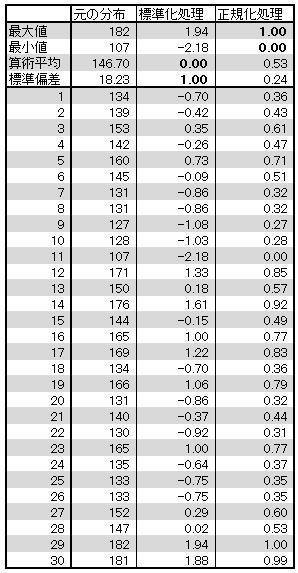
以下のサンプルデータを使って実際に計算してみます。ベースになるのは「元の分布」という列です。
元データ x(1), x(2), ... , x(n) を標準化するには以下の式を使います。各要素から平均値を引き、標準偏差 σ で割ります。
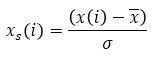
上の表を見ると標準化したデータは平均が0で標準偏差が 1 になっていることがわかりますね。
次は正規化です。元データ x(1), x(2), ... , x(n) を正規化するには以下の式を使います。分母は元データの最大値と最小値の引き算、つまりデータの幅を求めています。分子は各要素と最小値の引き算、つまり最小値が 0 になるように調整しています。

上の表を見ると正規化したデータは最大値が1、最小値が 0 になっていることがわかりますね。
最後に元データ、標準化したデータ、正規化したデータのヒストグラムを見てみましょう。

縦軸はどれも個数ですが、横軸のスケールが異なることに注意してください。標準化、正規化したことで横軸のスケールが変わっています。
最後に1つだけ白色化についても記載しておきます。複数の特徴量があるときにそれらが相関関係を持つ場合があります。特徴量の相関関係を無効化する処理を白色化と言います。
今回はG検定の用語対策として、標準化、正規化、正則化についてまとめてみました。それぞれしっかりと区別できるようにしてください。
では、ごきげんよう。
