G検定 / 統計検定 確率分布 #5

株式会社リュディアです。引き続き確率分布についてまとめていきます。

前回までの確率分布についてのまとめへのリンクは以下を参考にしてください。

今回は具体例として多項分布についてまとめてみます。前回の二項分布についてのまとめは事前に必ず目を通してください。

「はい」か「いいえ」かという試行を n 回実施したときの確率分布が二項分布に従うわけですが、これを一般の試行、つまり「はい」か「いいえ」だけでは無いような試行を n回実施したときの確率分布に拡張することを考えます。例えばサイコロを n回ふったときに出目の分布はどうなるかという確率分布を考えるわけです。この確率分布は多項分布に従います。

確率質量関数を見てみましょう。試行回数を n 回とします。また確率変数 Xのとりうる値を 1, 2, ..., k  の k種とします。また n 回の試行で各確率変数となった回数を x1, x2, ..., xk とします。最後に各確率変数の値の出現確率を p1, p2, ..., pk とします。このとき確率質量関数は以下のようになります。

サイコロの出目を例として具体的に見てみましょう。サイコロを n 回ふるとします。確率変数がとりうる値はサイコロの出目の種類なので k = 6 になります。またサイコロが均等であるとすると p1 = p2 = ... = 1/6 となります。x1, x2, ..., x6 は n 回の試行で実際に1, 2, ..., 6 が出た回数になります。確率質量関数に出てくる変数の具体的なイメージは捉えられましたか？

多項分布の平均と分散を以下に示しておきます。

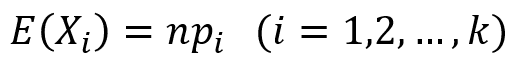
ちなみに多項分布で k = 2、つまり各試行で確率変数が取りうる値の種類 k = 2 の場合、多項分布は二項分布に一致します。実際、他項分布の確率質量関数で k = 2 とすると以下のように整理できます。

組合せ表記 nCr の部分は展開されていますが二項分布と一致していることがわかりますね。さらに n = 1 にするとベルヌーイ分布になりますが、これは前の記事のまとめでわかると思います。

G検定 / 統計検定 確率分布に関するまとめの続きは以下からどうぞ。

では、ごきげんよう。