G検定 停留点と鞍点

株式会社リュディアです。機械学習を最適化問題と捉えることは多く、G検定で停留点や鞍点に関する問題、特に正誤問題では頻出です。特に停留点は公式テキストである「白本」にキーワードも出ていないのでとまどいますね。今回は最適化問題と停留点、鞍点についてまとめてみます。

関数 f (x1, x2, ... , xn)  が与えられたとき、f が最小となるような (x1, x2, ... , xn) の組を求める問題を最小化問題と呼びます。最大化したい場合は符号を反転するだけなのでここでは最小化問題を扱います。

まず停留点についてです。停留点は臨界点とも呼びます。簡単化するため2変数関数 f ( x, y ) を考えます。停留点とは 2 変数関数 f ( x, y ) に対し

をみたす点 ( a , b ) のことを言います。関数 f を x で偏微分、関数 f を y で偏微分したものが 0 になる点を停留点と定義します。停留点とはどのような点なのでしょうか？結論から書くと以下の3つに「なりうる」候補が停留点です。

1. 関数 f の極大値をとる点 ( x, y )（極大点）
2. 関数 f の極小値をとる点 ( x, y )（極小点）
3. 鞍点 ( x, y )

つまり停留点は極大点、極小点、鞍点のいずれかになりうる点であるわけです。ここでは2変数関数であることと簡単化のため3分類としましたが厳密には「何とも判断できない点」という選択肢がありますが今回のまとめでは無視します。

ここからは具体的な数式とグラフでイメージを捉えてください。グラフは Wolfram alpha で生成しました。上記の 3 点を順にみていきましょう。

関数 f の極大値をとる点（極大点）についてみていきます。次の式とグラフをみてください。この数式は x = 0, y = 0 で極大値をとることがわかると思います。結果として最大値になるのですがここでは極大値とします。点 ( 0, 0 )は停留点であり、極大点でもあります。また f ( 0, 0 )は極大値となります。

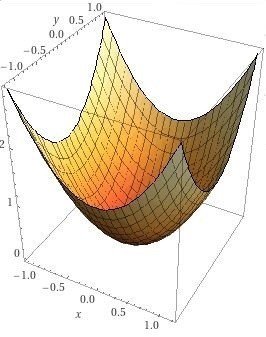
関数 f の極小値をとる点（極小点）についてみていきます。次の式とグラフをみてください。この数式は x = 0, y = 0 で極小値をとることがわかると思います。極大点の例で使ったグラフの符号を反転させたものです。結果論として最小値になるのですがここでは極小値とします。点 ( 0, 0 )は停留点であり、極小点でもあります。また f ( 0, 0 )は極小値となります。

鞍点についてみていきます。次の式とグラフをみてください。この数式は yを固定して x についてみると x = 0 で極小値になります。一方、x を固定して y についてみると y = 0 で極大値となります。( x, y ) = ( 0, 0) はどの方向から見るかによって、極小点にも極大点にもなります。それが鞍点です。

今回は停留点と鞍点、さらに極大点、極小点についてまとめてみました。G検定でも頻出分野のわりには公式テキストにものっていない内容があり、私も調べた記憶があります。皆さまのお役に立つようでしたら幸いでございます。

では、ごきげんよう