Python 複素数 #4

株式会社リュディアです。今回も Python で複素数を扱う方法についてまとめます。

前回までの Python で複素数を扱う方法についてのまとめへのリンクは以下を参考にしてください。

前回に引き続き複素数の特殊な演算や情報の取得についてまとめていきます。

複素数を使っていると極座標と関連付けて扱うことが多くあります。厳密には複素平面と極座標平面との行き来が多くなるということになります。

複素平面では複素数 c = a + bj を表す複素平面上での座標は (a, b) になります。これを極座標で扱うにはどのような情報が必要になるか考えるために以下の図を見てください。具体的な複素数として c = 3 + 5j を用います。

左側は通常の複素平面になります。横軸が実数軸、縦軸が虚数軸を表し c = 3 + 5j は (3, 5) という点として表現されます。右側は極座標で表現したものです。距離 r と偏角θで複素平面の例と同じ場所を表現しています。極座標で表現するためには r と θ の値が必要であることがわかりますね。

任意の複素数から r と θ を求める関数が polar() です。前回のまとめでは phase() を使って偏角を求めましたが polar() を使えば r とθをまとめて求めることが可能です。

import cmath

c = 3 + 5j

print(cmath.polar(c))

# (5.830951894845301, 1.0303768265243125)

また前回のまとめでは r を定義に従って求める、と記載しましたが何を言っていたのか以下の式で説明します。

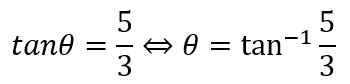
今回の例であれば tan を使えば θの値が求まることはわかりますね。これが定義に従えばという意味でこの定義通りの演算をしましたということです。また r も正面から計算するのであれば、以下のように計算可能であることもわかりますね。

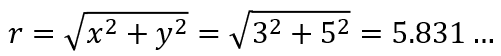
次は極座標から複素平面に戻す方法です。以下の例を見てください。

import cmath

c = 3 + 5j

r, theta = cmath.polar(c)
print(r, theta)

c1 = cmath.rect(r, theta)
print(c1)

#5.830951894845301 1.0303768265243125
#(3+5j)

まず関数 polar() で極座標の成分 r, theta に分割しています。次に極座標の成分 r, theta から元の複素数に戻す場合には関数 rect() を使います。実際 r, theta を rect() に渡すと元の c = 3 + 5j に戻っていることがわかりますね。

今回で Python で複素数を扱う方法についてのまとめはいったん終わりにします。

では、ごきげんよう。