G検定 コサイン類似度
株式会社リュディアです。今回はコサイン類似度についてまとめてみたいと思います。コサイン距離とも言われます
まずベクトルの内積から始めてます。高校の授業で習う2つの2次元ベクトルの内積は覚えてますか?2 つの 2 次元ベクトルを以下のように定義します。

この 2つのベクトルの内積は以下のように計算できましたね。
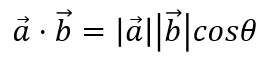
2つのベクトルの内積は2つのベクトルの大きさの掛け算と2つのベクトルのなす角をθとして上記の式で表現できます。2つのベクトルの間の・が内積を表す演算子になります。この式を以下のように変形してみます。

分子は内積をベクトルの成分で計算したものです。内積は 2つのベクトルの各成分の掛け算の和として表現できることを思い出してください。分母は 2つのベクトルの大きさの掛け算です。
今 2 つのベクトルが同じ向きである場合を考えます。たとえば 2 つのベクトルの成分が (1, 1) と (2, 2) であるとします。上記の式にあてはめると cosθ = 1 となります。
次に 2 つのベクトルのなす角が 90 度 = π/2 とします。たとえば 2 つのベクトルの成分が (1, 0) と (0, 2) であるとします。上記の式にあてはめると cosθ = 0 となります。
最後に 2 つのベクトルが逆向きである場合を考えます。たとえば 2 つのベクトルの成分が (-1, -1) と (2, 2) であるとします。上記の式にあてはめると cosθ = -1 となります。
結論としてはこの cosθ の計算式がコサイン類似度やコサイン距離と呼ばれるものです。n 次元ベクトルで再度考えてみます。2つの n次元ベクトルを以下のように定義します。

このときコサイン類似度を以下のように定義されます。

2次元で考えたときと同様に 2つのベクトルの向きが同じなら cosθ = 1、90度の角をなす場合は cosθ = 0 となります。2つのベクトルの向きが逆なら cosθ = -1 となります。
例えば文書の比較を行う際に各文書をベクトルの集合として表現しコサイン類似度を用いてどの程度似ているかの基準とします。コサイン類似度は -1 ~ +1 の値をとりますが文書比較で用いる場合は 0 ~ 1 の値を使う場合が多いです。1 のときに同一で 0 に近づくにつれて似ていないということになります。
では、ごきげんよう。
