ポケモンカードにおける確率について（統計データによるじゃんけんの勝率や採用枚数における確率など）

はじめに
こんにちは。
皆さんはポケカにおける構築やプレイの順番において考えるべきこと（それぞれの採用枚数に対しての確率や、必要アクションに対しての要求の成功率など）をその場の肌感でプレイしてはいませんか？
そういった人のために今回の記事ではポケカにおける一般的な確率についての解説や紹介を行いたいと思います。この記事は１プレイヤーの趣味のようなものなので気軽に内容の誤りへの指摘や質問などをしていただけると幸いです。
それでは、主題に入っていこうと思います。
（主がnoteに慣れておらず数式が拙くなりましたがご了承ください。）

じゃんけんについて
皆さんは普段考えてじゃんけんをされていますか？
主は何を言っているのだと思った方もいられるかもしれませんが、実はじゃんけんはすべての手が均等な勝率をしているわけではないのです。手の出し方によっても勝率は変化するためそのことについて紹介したいと思います。
桜美林大学の芳沢教授における研究（論文のリンクを貼ろうと思ったのですが見つからないのでネット記事をソースとして紹介させていただきます。https://president.jp/articles/-/79230?page=2 ）によって統計的なデータにおけるじゃんけんには以下のことが分かっています。
１．初めに出す手の内訳としてはグーが約35％、チョキーが約32％、パーが約33％であること。
２．同じ手を二回連続で出す割合は約23％となっていること。

上の二点からじゃんけんを統計データに基づいて行うときの最適化計算を行う。ただし、あいことなった後は0.77×（1.の比率）であると仮定します。

2. からじゃんけんを「最初はグー」の掛け声で始める際、出される手が統計データに基づいくなら相手の手からは初手はパーかチョキが77％ででることになります。そのためはじめにチョキを出し、あいこであるならパーその次はグーという風にあいことなった手に負ける手を出し続ければ勝率は高まります。
この方法を手段Aと呼びます。

ここで簡単のため3回目までに決着がつくじゃんけんを考えます。手段Aを遂行したときの勝率（勝率＝3回目までに勝利する確率/3回目までに決着する確率）を求めます。ただし相手の出る手は上の統計データに従うとします。

このときの求める確率をpとしたとき

$${ p = \frac{0.77 \cdot \frac{33}{65} + 0.77^2 \cdot \frac{32}{65} \cdot \frac{35}{68} + 0.77^3 \cdot \frac{32}{65} \cdot \frac{33}{68} \cdot \frac{32}{67}}{1 - 0.77^3 \cdot \frac{32}{65} \cdot \frac{33}{68} \cdot \frac{35}{67}} = 0.6291 }$$

となります。
仮定の中での結果ではありますが、手段Aの勝率約63％となりました。
また最初はグーで始めない場合約54％になりました。

上の結果を踏まえて、皆さんも統計上一番勝てる手段Aを試してみてはいかがでしょうか。

採用枚数について
皆さんは採用枚数についてどのような認識でいますか？
私は採用枚数ごとのサイド落ち確率や初手の手札に来る確率などのある程度の数値を捉えることが構築を組む上での指標を増やすことにつながると思います。
そこでポケカにおける確率の数値を捉えていただくために以下にポケカのデッキを構築する上で上で多く起こる事象を列挙させていただきます。

1. ピン刺し（1枚採用）のサイド落ち確率p1
$${ p_1 = \frac{{\binom{59}{5}}}{{\binom{60}{6}}} = 0.10 }$$
約10％

2. 2枚採用の2枚サイド落ち確率p2
$${ p_2 = \frac{{\binom{58}{4}}}{{\binom{60}{6}}} = 0.00847 }$$
約0.847％
2枚に増やすだけでここまでサイド落ちをケアできるのはうれしいですね。
僕はボムドラパのリストでヨノワールを2枚で利用するのですが、これは確実に1回は（約99％で）ゲーム中にヨノワールのカーストボムを撃ちたいからですね。

3.4枚採用のカードがはじめの手札7枚＋トップの1枚の合計8枚の中に最低一枚ある確率p3
$${ p_3 = 1 - \frac{{\binom{56}{8}}}{{\binom{60}{8}}} = 0.4448 }$$
約44.48％

4.8枚採用（4枚採用×２）（ex ペパー４ポフィン４）のカードたちがはじめの手札7枚＋トップの1枚の合計8枚の中に最低一枚ある確率p4
$${ p_4 = 1 - \frac{{\binom{52}{8}}}{{\binom{60}{8}}} = 0.7005 }$$
約70.05％

5.12枚採用(4枚採用×3)のカードたちがはじめの手札7枚＋トップの1枚の合計8枚の中に最低1枚ある確率p5
$${ p_5 = 1 - \frac{{\binom{48}{8}}}{{\binom{60}{8}}} = 0.8525 }$$
約85.25％

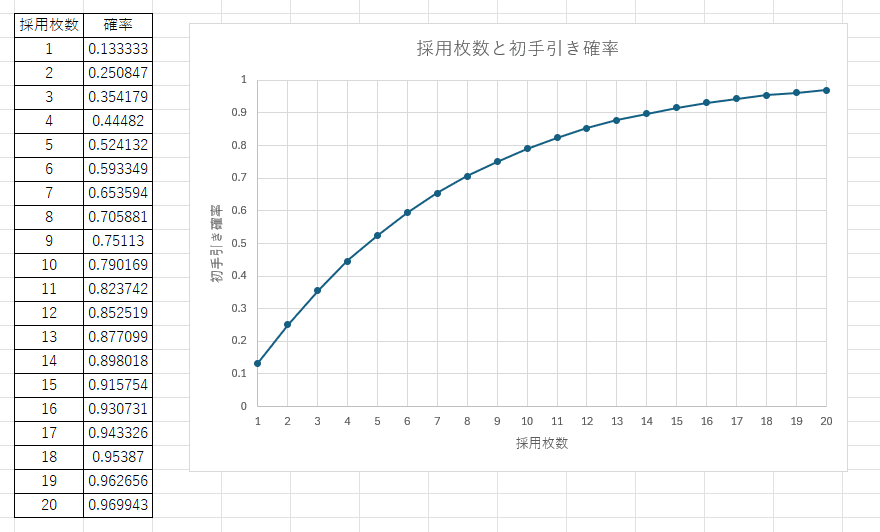
3.～5.のようなある枚数aに対しての最初の手札に来る確率をp(a)としてグラフ化しました。

excelで出力した結果です。

まあ　
$${ 1 - \frac{{\binom{60-x}{8}}}{{\binom{60}{8}}} }$$
のグラフなのでこんな感じにはなりますよね。
初手に来る確率が7割を超えるのは8枚から
初手に来る確率が8割を超えるのは11枚から
初手に来る確率が9割を超えるのは15枚からとなっています。
厳密には初手で山を掘ることのできるカード（ex ポケストップ トレッキングシューズ）や初めの7枚の中に2枚たねポケモンがいないと枚数にカウントできない召喚時効果カード（ex ネオラントV）などがあるので計算が難しくなりますが指標にはなると思います。

まとめ
ここまで読んでいただいたかたありがとうございました。最後に実践編として問題を出して終わろうと思います。面白かったという人はぜひ問題に挑戦してみてください。（結構難しく作ったつもりです）

問）以下のキャリードラパのリストで手段Aを行いじゃんけんをして、後1でプレシャスキャリーを打てる確率はどれくらいか？
（ただし、手段Aのじゃんけんの勝率は63％であり、先攻をとりたいプレイヤーと後攻をとりたいプレイヤーの割合は 1 : 1とする。)
（ただし簡単のため今回の問いにおいて使用できるカードは プレシャスキャリー , ペパー , 森の封印石 , ハイパーボール , すべてのたねポケモンの現物
に限るとする。ナンジャモは計算がグロくなるので外しました。）

解答はこの記事を拡散していただけると見れる仕組みにしますので、よかったらtwitter(新X)フォローと該当ツイートのリツイートをお願いします。

twitter(新X)⇒https://x.com/lupiapoke?s=21