
スプリンターズステークス(GⅠ)2024年9月29日 中山競馬11R JRA| 払戻金の相場をデータ分析
競馬の予測や戦略を考える上で、この記事は非常に有益な情報を提供しています。過去の同じレースにおける馬券の払戻金を基に、統計的な相場を解析した結果を紹介し、レースの払戻金やオッズの目安に活用できます。また、レースが荒れる可能性があるかどうかを判断するための手がかりとしても利用できる内容となっています。
はじめに
■グラフの読み方
払戻金を対数変換して確率密度で比較
・内容:本レースと同じクラス・馬場条件での払戻金の確率密度を比較しています。
・解釈:横軸は対数変換された払戻金、縦軸は確率密度を示しています。払戻金の対数値が大きいほど、払戻金は高くなります。確率密度が高い場合、その払戻金が頻繁に発生していることを意味します。分布のピークに顕著な差があるか、または分布が低配当や高配当に偏っているかを確認することができます。
分析結果
単勝の払戻金
単勝払戻金を対数変換して、同クラス・馬場と確率密度で比較
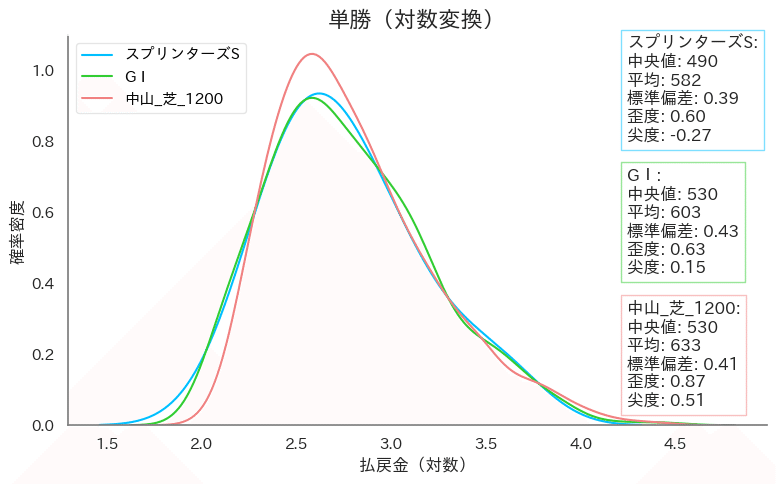
中央値と平均値:
スプリンターズSの中央値(490)はG1(530)および中山 芝1200m(530)より低いです。これは、スプリンターズSの払戻金が他のレースに比べて中程度の値が少ないことを示しています。
スプリンターズSの平均値(582)は、G1(603)および中山 芝1200m(633)より低くなっています。これは、高額配当の発生頻度が他のカテゴリーより低いことを示唆しています。
標準偏差(データのばらつき):
スプリンターズSの標準偏差は0.39で、G1(0.43)より小さく、中山 芝1200m(0.41)とほぼ同等です。
これは、スプリンターズSの払戻金のばらつきがG1よりも小さく、中山 芝1200mとほぼ同程度であることを示しています。
歪度(データの偏り):
スプリンターズSの歪度は0.60で、G1(0.63)より若干低く、中山 芝1200m(0.87)よりも大幅に低いです。
これは、スプリンターズSの払戻金分布が他の2つのカテゴリーよりもやや対称的であることを示しています。
尖度(データの集中度):
スプリンターズSの尖度は-0.27で、G1(0.15)および中山 芝1200m(0.51)よりも低いです。
これは、スプリンターズSの払戻金分布が他の2つのカテゴリーよりも平坦で、極端な値が少ないことを示しています。
同じクラス(G1)と比較:
スプリンターズSの中央値(490)はG1全体の中央値(530)よりも低く、平均値(582)もG1全体の平均値(603)よりも低いです。
払戻金の分布を見ると、スプリンターズSは同じG1クラスの他のレースと比較して、払戻金が低めであり、ばらつきが少なく、払戻金が均等に分布している傾向があります。
同じ馬場(中山 芝1200m)と比較:
スプリンターズSの中央値(490)は中山 芝1200mの中央値(530)よりも低く、平均値(582)も中山 芝1200mの平均値(633)よりも低いです。
払戻金の分布を見ると、スプリンターズSの払戻金は中山 芝1200mのレースと比較して、全体的に低く、ばらつきが少なく、極端な値が発生しにくい傾向があることがわかります。
結論
スプリンターズSは他のG1レースや中山 芝1200mのレースと比べて、中央値と平均値が共に低いことから、払戻金が全体的に低い傾向にあることが示唆されます。
また、標準偏差が小さいことに加えて、歪度が低く、尖度が負であることから、払戻金の分布が比較的対称的で平坦であり、極端に高額または低額な払戻金が少なく、安定していることがわかります。
よって、スプリンターズSの払戻金は全体として低く、安定傾向にあるといえます。
枠連の払戻金
枠連払戻金を対数変換して、同クラス・馬場と確率密度で比較

中央値と平均値:
スプリンターズSの中央値(1,130)はG1(1,150)および中山 芝1200m(1,220)より低いです。これは、スプリンターズSの枠連払戻金が他のレースに比べて中程度の値が少ないことを示しています。
スプリンターズSの平均値(1,137)は、G1(1,278)および中山 芝1200m(1,303)より低くなっています。これは、高額配当の発生頻度が他のカテゴリーより低いことを示唆しています。
標準偏差(データのばらつき):
スプリンターズSの標準偏差は0.34で、G1(0.39)および中山 芝1200m(0.42)よりも小さいです。
これは、スプリンターズSの枠連払戻金のばらつきが他の2つのカテゴリーよりも小さいことを示しています。
歪度(データの偏り):
スプリンターズSの歪度は0.46で、G1(0.58)および中山 芝1200m(0.43)と比較して中間的な値です。
これは、スプリンターズSの枠連払戻金分布が他の2つのカテゴリーと同程度の偏りを持っていることを示しています。
尖度(データの集中度):
スプリンターズSの尖度は-0.32で、G1(0.35)よりも低く、中山 芝1200m(-0.11)よりもさらに低いです。
これは、スプリンターズSの枠連払戻金分布が他の2つのカテゴリーよりも平坦で、極端な値が少ないことを示しています。
同じクラス(G1)と比較:
スプリンターズSの中央値(1,130)はG1全体の中央値(1,150)よりも低く、平均値(1,137)もG1全体の平均値(1,278)よりも低いです。
払戻金の分布を見ると、スプリンターズSは同じG1クラスの他のレースと比較して、枠連払戻金が低めであり、ばらつきが少なく、払戻金が均等に分布している傾向があります。
同じ馬場(中山 芝1200m)と比較:
スプリンターズSの中央値(1,130)は中山 芝1200mの中央値(1,220)よりも低く、平均値(1,137)も中山 芝1200mの平均値(1,303)よりも低いです。
払戻金の分布を見ると、スプリンターズSの枠連払戻金は中山 芝1200mのレースと比較して、全体的に低く、ばらつきが少なく、極端な値が発生しにくい傾向があることがわかります。
結論
スプリンターズSは他のG1レースや中山 芝1200mのレースと比べて、中央値と平均値が共に低いことから、枠連払戻金が全体的に低い傾向にあることが示唆されます。
また、標準偏差が小さいことに加えて、歪度が中間的で、尖度が最も低いことから、枠連払戻金の分布が比較的対称的で平坦であり、極端に高額または低額な払戻金が少なく、安定していることがわかります。
よって、スプリンターズSの枠連払戻金は全体として低く、安定傾向にあるといえます。
馬連の払戻金
馬連払戻金を自然対数変換して、同クラス・馬場と確率密度で比較

中央値と平均値:
スプリンターズSの中央値(2,140)はG1(2,335)および中山 芝1200m(2,290)より低いです。これは、スプリンターズSの馬連払戻金が他のレースに比べて中程度の値が少ないことを示しています。
スプリンターズSの平均値(2,173)は、G1(2,733)および中山 芝1200m(2,611)より低くなっています。これは、高額配当の発生頻度が他のカテゴリーより低いことを示唆しています。
標準偏差(データのばらつき):
スプリンターズSの標準偏差は0.49で、G1(0.54)および中山 芝1200m(0.56)よりも小さいです。
これは、スプリンターズSの馬連払戻金のばらつきが他の2つのカテゴリーよりも小さいことを示しています。
歪度(データの偏り):
スプリンターズSの歪度は0.11で、G1(0.49)および中山 芝1200m(0.58)よりも大幅に低いです。
これは、スプリンターズSの馬連払戻金分布が他の2つのカテゴリーよりもかなり対称的であることを示しています。
尖度(データの集中度):
スプリンターズSの尖度は-1.21で、G1(-0.09)および中山 芝1200m(0.23)よりもかなり低いです。
これは、スプリンターズSの馬連払戻金分布が他の2つのカテゴリーよりもかなり平坦で、極端な値が少ないことを示しています。
同じクラス(G1)と比較:
スプリンターズSの中央値(2,140)はG1全体の中央値(2,335)よりも低く、平均値(2,173)もG1全体の平均値(2,733)よりも大幅に低いです。
払戻金の分布を見ると、スプリンターズSは同じG1クラスの他のレースと比較して、馬連払戻金が低めであり、ばらつきが少なく、払戻金が非常に均等に分布している傾向があります。
同じ馬場(中山 芝1200m)と比較:
スプリンターズSの中央値(2,140)は中山 芝1200mの中央値(2,290)よりも低く、平均値(2,173)も中山 芝1200mの平均値(2,611)よりも大幅に低いです。
払戻金の分布を見ると、スプリンターズSの馬連払戻金は中山 芝1200mのレースと比較して、全体的に低く、ばらつきが少なく、極端な値が発生しにくい傾向が非常に強いことがわかります。
結論
スプリンターズSは他のG1レースや中山 芝1200mのレースと比べて、中央値と平均値が共に大幅に低いことから、馬連払戻金が全体的にかなり低い傾向にあることが示唆されます。
また、標準偏差が小さいことに加えて、歪度が非常に低く、尖度が大幅に負であることから、馬連払戻金の分布が非常に対称的で平坦であり、極端に高額または低額な払戻金が非常に少なく、非常に安定していることがわかります。
よって、スプリンターズSの馬連払戻金は全体として低く、非常に安定傾向にあるといえます。
馬単の払戻金
馬単払戻金を対数変換して、同クラス・馬場と確率密度で比較

中央値と平均値:
スプリンターズSの中央値(4,010)はG1(4,440)および中山 芝1200m(4,260)より低いです。これは、スプリンターズSの馬単払戻金が他のレースに比べて中程度の値が少ないことを示しています。
スプリンターズSの平均値(4,132)は、G1(5,116)および中山 芝1200m(4,995)より大幅に低くなっています。これは、高額配当の発生頻度が他のカテゴリーより明らかに低いことを示唆しています。
標準偏差(データのばらつき):
スプリンターズSの標準偏差は0.54で、G1(0.57)および中山 芝1200m(0.57)よりもわずかに小さいです。
これは、スプリンターズSの馬単払戻金のばらつきが他の2つのカテゴリーよりもやや小さいことを示しています。
歪度(データの偏り):
スプリンターズSの歪度は0.18で、G1(0.44)および中山 芝1200m(0.58)よりも大幅に低いです。
これは、スプリンターズSの馬単払戻金分布が他の2つのカテゴリーよりもかなり対称的であることを示しています。
尖度(データの集中度):
スプリンターズSの尖度は-0.95で、G1(-0.09)および中山 芝1200m(0.24)よりもかなり低いです。
これは、スプリンターズSの馬単払戻金分布が他の2つのカテゴリーよりもかなり平坦で、極端な値が少ないことを示しています。
同じクラス(G1)と比較:
スプリンターズSの中央値(4,010)はG1全体の中央値(4,440)よりも低く、平均値(4,132)もG1全体の平均値(5,116)よりも大幅に低いです。
払戻金の分布を見ると、スプリンターズSは同じG1クラスの他のレースと比較して、馬単払戻金が低めであり、ばらつきがやや少なく、払戻金がより均等に分布している傾向があります。
同じ馬場(中山 芝1200m)と比較:
スプリンターズSの中央値(4,010)は中山 芝1200mの中央値(4,260)よりも低く、平均値(4,132)も中山 芝1200mの平均値(4,995)よりも大幅に低いです。
払戻金の分布を見ると、スプリンターズSの馬単払戻金は中山 芝1200mのレースと比較して、全体的に低く、ばらつきがやや少なく、極端な値が発生しにくい傾向が強いことがわかります。
結論
スプリンターズSは他のG1レースや中山 芝1200mのレースと比べて、中央値と平均値が共に大幅に低いことから、馬単払戻金が全体的にかなり低い傾向にあることが示唆されます。
また、標準偏差がわずかに小さいことに加えて、歪度が非常に低く、尖度が大幅に負であることから、馬単払戻金の分布が非常に対称的で平坦であり、極端に高額または低額な払戻金が少なく、非常に安定していることがわかります。
よって、スプリンターズSの馬単払戻金は全体として低く、非常に安定傾向にあるといえます。
3連複の払戻金
3連複払戻金を対数変換して、同クラス・馬場と確率密度で比較

中央値と平均値:
スプリンターズSの中央値(11,660)はG1(7,985)および中山 芝1200m(7,450)よりも大幅に高いです。これは、スプリンターズSの3連複払戻金が他のレースに比べて中程度の値が多いことを示しています。
スプリンターズSの平均値(11,203)も、G1(9,300)および中山 芝1200m(8,118)より高くなっています。これは、高額配当の発生頻度が他のカテゴリーより高いことを示唆しています。
標準偏差(データのばらつき):
スプリンターズSの標準偏差は0.68で、G1(0.67)とほぼ同等で、中山 芝1200m(0.62)よりもやや大きいです。
これは、スプリンターズSの3連複払戻金のばらつきが他の2つのカテゴリーと同程度かやや大きいことを示しています。
歪度(データの偏り):
スプリンターズSの歪度は0.35で、G1(0.65)および中山 芝1200m(0.39)よりも低いです。
これは、スプリンターズSの3連複払戻金分布が他の2つのカテゴリーよりもやや対称的であることを示しています。
尖度(データの集中度):
スプリンターズSの尖度は-0.04で、G1(0.37)および中山 芝1200m(-0.12)の中間的な値です。
これは、スプリンターズSの3連複払戻金分布が他の2つのカテゴリーと比較して、極端な値の発生頻度が中程度であることを示しています。
同じクラス(G1)と比較:
スプリンターズSの中央値(11,660)はG1全体の中央値(7,985)よりも大幅に高く、平均値(11,203)もG1全体の平均値(9,300)よりも高いです。
払戻金の分布を見ると、スプリンターズSは同じG1クラスの他のレースと比較して、3連複払戻金が高めであり、ばらつきはほぼ同等で、払戻金の分布がやや対称的である傾向があります。
同じ馬場(中山 芝1200m)と比較:
スプリンターズSの中央値(11,660)は中山 芝1200mの中央値(7,450)よりも大幅に高く、平均値(11,203)も中山 芝1200mの平均値(8,118)よりも大幅に高いです。
払戻金の分布を見ると、スプリンターズSの3連複払戻金は中山 芝1200mのレースと比較して、全体的に高く、ばらつきがやや大きく、払戻金の分布がやや対称的である傾向があることがわかります。
結論
スプリンターズSは他のG1レースや中山 芝1200mのレースと比べて、中央値と平均値が共に大幅に高いことから、3連複払戻金が全体的にかなり高い傾向にあることが示唆されます。
また、標準偏差が同程度かやや大きいことに加えて、歪度が低く、尖度が中間的であることから、3連複払戻金の分布がやや対称的で、極端な値の発生が中程度であることがわかります。
よって、スプリンターズSの3連複払戻金は全体として高く、やや荒れる傾向にあるといえます。
3連単の払戻金
3連単払戻金を対数変換して、同クラス・馬場と確率密度で比較

中央値と平均値:
スプリンターズSの中央値(50,820)はG1(42,410)および中山 芝1200m(41,270)よりも大幅に高いです。これは、スプリンターズSの3連単払戻金が他のレースに比べて中程度の値が多いことを示しています。
スプリンターズSの平均値(58,500)も、G1(48,387)および中山 芝1200m(48,129)より大幅に高くなっています。これは、高額配当の発生頻度が他のカテゴリーより高いことを示唆しています。
標準偏差(データのばらつき):
スプリンターズSの標準偏差は0.72で、G1(0.73)とほぼ同等で、中山 芝1200m(0.68)よりもやや大きいです。
これは、スプリンターズSの3連単払戻金のばらつきが他の2つのカテゴリーと同程度かやや大きいことを示しています。
歪度(データの偏り):
スプリンターズSの歪度は0.25で、G1(0.55)および中山 芝1200m(0.37)よりも低いです。
これは、スプリンターズSの3連単払戻金分布が他の2つのカテゴリーよりもやや対称的であることを示しています。
尖度(データの集中度):
スプリンターズSの尖度は-0.41で、G1(0.27)および中山 芝1200m(-0.10)よりも低いです。
これは、スプリンターズSの3連単払戻金分布が他の2つのカテゴリーよりも平坦で、極端な値が少ないことを示しています。
同じクラス(G1)と比較:
スプリンターズSの中央値(50,820)はG1全体の中央値(42,410)よりも大幅に高く、平均値(58,500)もG1全体の平均値(48,387)よりも大幅に高いです。
払戻金の分布を見ると、スプリンターズSは同じG1クラスの他のレースと比較して、3連単払戻金が高めであり、ばらつきはほぼ同等で、払戻金の分布がより対称的で平坦である傾向があります。
同じ馬場(中山 芝1200m)と比較:
スプリンターズSの中央値(50,820)は中山 芝1200mの中央値(41,270)よりも大幅に高く、平均値(58,500)も中山 芝1200mの平均値(48,129)よりも大幅に高いです。
払戻金の分布を見ると、スプリンターズSの3連単払戻金は中山 芝1200mのレースと比較して、全体的に高く、ばらつきがやや大きく、払戻金の分布がより対称的で平坦である傾向があることがわかります。
結論
スプリンターズSは他のG1レースや中山 芝1200mのレースと比べて、中央値と平均値が共に大幅に高いことから、3連単払戻金が全体的にかなり高い傾向にあることが示唆されます。
また、標準偏差が同程度かやや大きいことに加えて、歪度が低く、尖度が負であることから、3連単払戻金の分布がより対称的で平坦であり、極端な値の発生が比較的少ないことがわかります。
よって、スプリンターズSの3連単払戻金は全体として高く、やや荒れる傾向にあるものの、極端な高配当は比較的少ないといえます。
Amazonアソシエイト・プログラムに参加しております。
記事内に掲載している商品は広告リンクです。
傾向と対策
スプリンターズSは、他のG1レースや中山芝1200mのレースと比較して、払戻金に以下の特徴があります。
単勝:払戻金が低く、安定した傾向
枠連:払戻金が低く、安定した傾向
馬連:払戻金が低く、安定した傾向
馬単:払戻金が低く、安定した傾向
3連複:払戻金が高く、やや荒れる傾向
3連単:払戻金が高く、やや荒れる傾向
総評
スプリンターズSは、全体的に払戻金が低いレースですが、3連複と3連単に関しては高い払戻金が見られ、特に3連単ではやや荒れる傾向が確認できます。他のG1レースや中山芝1200mのレースと比べると、安定性が高い一方で、3連系の馬券では高額配当が発生しやすい特徴が見られます。
払戻金の比較

この分析を通じて、競馬のデータ分析が初めての方でも、レースの予想や馬券の選択に役立てていただけることを期待しています。
興味を持っていただけましたら、フォローしていただくと、AIの制作モチベーションが上がります。
#競馬
#JRA
#中央競馬
#競馬予想
#競馬AI
#競馬AI予想
この記事が気に入ったらサポートをしてみませんか?
