知識ゼロの未経験がpythonで株価予測ができるようになりました。
はじめに
パソコンもろくに触ったとがない、未経験が時系列データの分析、株価予測に挑戦しました。少しでも興味がある方や、初学者にとってぜひ参考になれば幸いです。
きっかけ
私が興味を持ったきっかけは、あるinstagramの投稿で「pythonによる株価の予測」というものを見て、自分もやりたい!と思い、何の知識もなく、何から始めたらいいのか分からず、Google先生に聞いてみたところ、Aidemy(プログラミングスクール)を見つけ受講することになりました。
概要
Pythonで時系列データを分析
LSTMを活用
実行環境
Google Colab
Intel Mac
LSTMとは
LSTMとは(Long-Short Term Memory:長短期記憶ユニット)とは、
RNN(Recurrent Neural Network:再帰型ネットワーク)の一つです。
主に時系列データの解析に用いられ、例えば、翻訳や言語解析や音声の解析、
売上予測などに多様されています。
LSTMを使うメリット・ポイントとして、
LSTMは長期的な依存関係を学習できるため、時系列データなどの長期的なパターンを捉えるのに優れています。
LSTMは非線形な関係をモデル化できるため、データの複雑なパターンを捉えることができます。
LSTMはモデルの層をスタックすることで、深いネットワークを構築できるため、高い表現能力を持ちます。
LSTMはメモリセルを持ち、過去の情報を保持しながら新しい情報を学習することができます。
LSTMは過去の情報を保持し、長期的な予測を行うことができるため、将来のトレンドやパターンを捉えて予測を行うことができます。
全体の流れ
データの取得
目的変数の追加、下準備
全体像を掴むため可視化
データの準備、特徴量を追加する
学習データと検証データに分割する
LSTMで予測
作成したモデルが本当に予測に使えるかどうか確認するために、交差検証を行う
予測結果と正解結果を混同行列を用いて確認
・データの取得・確認
yfinanceインストール(Yahoo! Financeから情報を取得するためのAPI)
pip install yfinance今回はamazon(コード:AMZN)の株価予測をしていきたいと思います。
株価の銘柄については以下より確認できます。
日本取引所グループ
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import datetime
import yfinance as yf
#ターゲットを指定
ticker = "AMZN"
#データを収集
data = yf.download(ticker, start= "2003-01-01",end="2023-03-15", interval = "1d")
df = data
#追加
df["Date"] = df.index
df = df.reset_index(drop=True)
df = df.drop("Volume", axis=1)
df_tmp = df.drop("Date",axis=1)
#可視化する
df_tmp.plot()
df
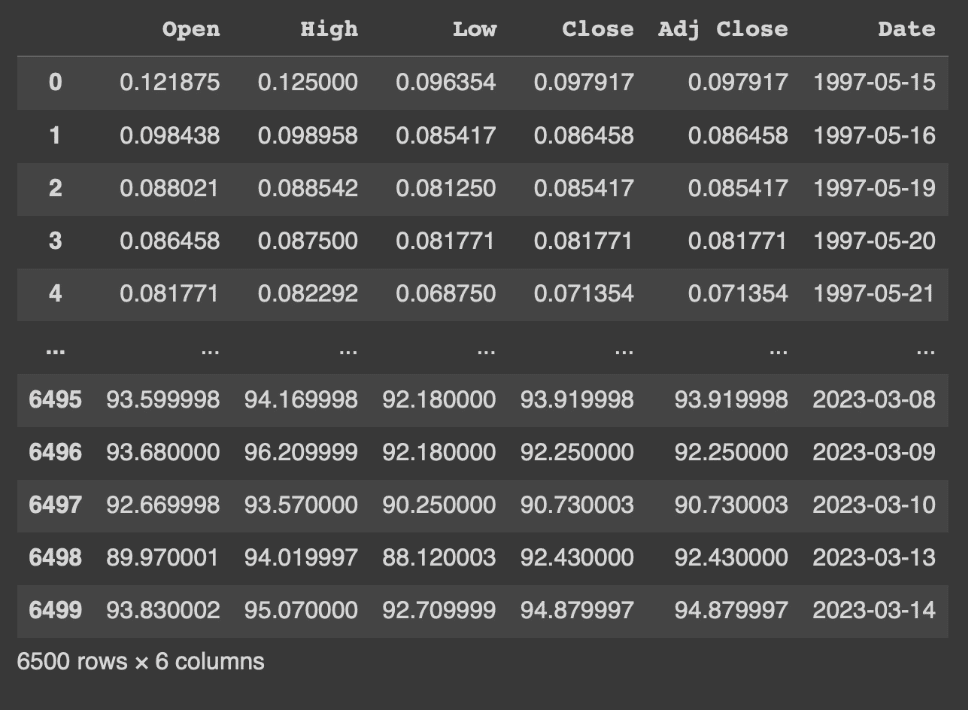
インデックスが0から6499までの連番で、カラムに
日付('Date')、最高値('High')、最安値('Low')、始値('Open')、終値('Close')が設定されたデータフレームである事が確認できます。
日付('Date)は指定した範囲で1980年1月1日から2023年3月15日までとなっています。(好きな範囲で日付の部分は指定してください。)
その後、'info'メソッドを用いて、欠損値の有無やカラムのデータの方を確認します。
df.info()
出力結果から、各カラム欠損値なしであることがわかります。
次に、曜日情報のカラムを追加します。'datetime64'型は'dt.weekday'メソッドを用いて、曜日情報を取得する事ができます。月曜日を0として連番の数字を設定されます。
# 曜日情報を追加(月曜:0, 火曜:1, 水曜:2, 木曜:3, 金曜:4、土曜:5、日曜:6)
df['weekday'] = df['Date'].dt.weekday
df
'weekday'のカラムが追加され0から4の数字が入力されている事がわかります。
また、株取引の行われない土曜日:5と日曜日:6のデータは存在していない事もわかります。
日付の情報の'Date','weekday','weeks'のカラムが分かれて表示されているので、見栄えを整理する目的で、一旦カラムの並び替えを行います。
先頭に日付の情報をまとめます。
並び替えたい順序でカラムを記述しdfを置き換えます。
実行する事で、並び替えられている事がわかります。
# カラムの並べ替え
df = df[['Date', 'weeks', 'weekday', 'High', 'Low', 'Open', 'Close']]念の為にsort_valuesメソッドを使って日付順に並び替えを行います。
# データの並び替え
df.sort_values(by='Date', ascending=True, inplace=True)次に今回予測したい翌日の終値が本日の終値よりも上がるのかどうかの情報を追加します。shiftメソッドを用いてカラムの情報をずらすdfを作成する事ができるので、それを用いて計算を行います。
shift(-1)とする事で、カラムの情報を1行上にずらしたデータフレームを作成する事ができます。
dfを1行分上にずらしたものをdf_shiftとして作成します。一番下のカラムは欠損値となります。
#カラム情報を1行上にずらしたデータフレームを作成する
df_shift = df.shift(-1)このdf_shiftを用いて、翌日の終値と本日の終値を引き算し、その結果を'delta_Close'というカラムを追加しdfに入力します。
#翌日の始値と本日の終値の差分を追加する
df['delta_Close'] = df_shift['Close'] - df['Close']この'delta_Close'が上がる場合1、それ以外を0として目的変数となる'Up'のカラムを追加します。同時に'delta_Close'カラムの削除も行います。
#目的変数Upを追加する(翌日の終値が上がる場合1、それ以外は0とする)、'delta_Close'カラムの削除
df['Up'] = 0
df['Up'][df['delta_Close'] > 0] = 1
df = df.drop('delta_Close', axis=1)ここまでで、下準備となる週番号、曜日、目的変数の追加が終わりました。
・全体像を掴む
時系列データをグラフで表示する事で、株価変動の大まかなイメージを掴みます。
'Open', 'High', 'Low', 'Close'を抜き出しdf_newを作成後に、pyplotを用いてグラフ化行います。
matplotlibのライブラリからpyplotをpltという名前でインポートします。
df_newにplotメソッドを用いて、引数'kind=line'とする事で折れ線グラフが作成されます。pyplotのshowメソッドでグラフを表示します。
#データの全体像を掴む。
# 'Open', 'High', 'Low', 'Close'グラフ化のためにカラム抽出
df_new = df[['Open', 'High', 'Low', 'Close']]
# matplotlibのインポート
from matplotlib import pyplot as plt
# 時系列折れ線グラフの作成
df_new.plot(kind='line')
plt.show()
2022年頃まで、上昇傾向にあり、以降は下降していることがわかります。
・特徴量の追加
予測を正しく行えるようにする為の情報量(特徴量)を追加します。現在dfに入っている始値、終値、最高値、最安値の情報だけを用いて予測する事も可能ですが、株価の変動に影響すると言われている一般的な情報を追加していきます。
終値の前日比率と、始値と終値の差分カラムに追加します。
まず終値の前日比率ですが、本日の終値が前日から何%変動したのかを表す値となります。
(今日の終値 - 前日の終値) ÷ 前日の終値
で計算します。
shiftメソッドを用いて、今度は1行したにずらしたデータフレームを作成し、終値の前日比率'Close_ratio'を計算しdfにカラムを追加します。
#特徴量を追加する。
# 終値の前日比の追加
df_shift = df.shift(1)
df['Close_ratio'] = (df['Close'] - df_shift['Close']) / df_shift['Close']次に、始値と終値の差分'Body'をdfに追加します。
# 始値と終値の差分を追加
df['Body'] = df['Open'] - df['Close']特徴量の追加は以上になります。次に、不要なデータの削除を行います。今回、月曜日から木曜日までの情報を用いて、金曜日の始値が上がるか下がるのかを予測するモデルを作成するために、各週で月曜日から金曜日までのデータが揃っている週だけ使用します。祝日や年末年始など株取引が行われていない日はデータがない為、5日分のデータが揃っていない週が存在しています。
各週毎に何日分のデータが存在しているのかを調べて、5日分揃っている週のデータを持ってきます。
手順としては、週番号'weeks'のリストを作成します。その後リストから取り出した同じ週番号のデータ数をカウントして行き結果をdfに格納し、5日揃っている週だけ残す処理をします。
週番号は1688から3036まで連番で有ると考えられ、1688から順番に処理すれば良いと考えられますが、万が一抜けている週が存在して居ても処理が行えるように、あえて週番号を抜き出したリスト(list_weeks)を作成します。
#次に、不要なデータの削除を行います。。
#月曜日から金曜日までのデータが揃っている週を使用します
# 週番号をリストに格納
list_weeks = []
list_weeks = df['weeks'].unique()
list_weeks出力結果>>>
array([1688, 1689, 1690, ..., 3034, 3035, 3036])リストに従い、for文を用いて、週毎の日数をカウントしたカラム'week_days'にカウント数を入力します。
# 各週ごとの日数を入力
df['week_days'] = 0
for i in list_weeks:
df['week_days'][df['weeks'] == i] = len(df[df['weeks'] == i])
df
5日データの存在する週(week_daysが5)の週のデータを抜き出して、dfに入力します。
#5日データの存在する週(week_daysが5)の週のデータを抜き出して、dfに入力します。
# 月曜〜金曜まで5日分データのある週だけデータを取り出す
df = df[df['week_days'] == 5]予測に使用しない金曜日のデータ(weekdayが4)を削除します。
#予測に使用しない金曜日のデータ(weekdayが4)を削除します。
#金曜日のデータを削除する(weekday:4となるデータ)
df = df[df['weekday'] != 4]不要カラムの削除と並び替えを行います。
不要カラムの削除と、並び替えを行います
# 不要カラムの削除と並べ替え
df = df[['weekday', 'High', 'Low', 'Open', 'Close', 'Close_ratio', 'Body', 'Up']]ここまでで、データの準備は完了です
・学習データと検証データに分割
ここからは、2003年以降のデータを使用します。
2003年から2020年を学習データ、2021年以降を検証データとして分割します。
#学習データと検証データに分割する
# 学習データを2003-01-01〜2020-12-31の期間としdf_trainに入力する
df_train = df['2003-01-01' : '2020-12-31']2021年1月1日以降のデータを抜き出し、df_valに入力します。
# 検証データを2021-01-01以降としてとしてdf_valに入力する
df_val = df['2021-01-01' : ]学習データと検証データをそれぞれ、説明変数と目的変数に分けます。
説明変数のカラムは'weekday', 'High', 'Low', 'Open', 'Close', 'Close_ratio', 'Body'を
目的変数のカラムは'Up'になります。
学習データの説明変数をX_train、学習データの目的変数をy_trainとしてカラムを指定して、それぞれを入力します。また、表示することでX_train, y_trainそれぞれに指定した期間内のデータが入力されていることが分かります。
# 学習データを説明変数(X_train)と目的変数(y_train)に分ける
X_train = df_train[['weekday', 'High', 'Low', 'Open', 'Close', 'Close_ratio', 'Body']]
y_train = df_train['Up']
# 学習データの説明変数と目的変数を確認
print(X_train)
print(y_train)
同様に検証データの説明変数をX_val、目的変数をy_valとしてデータを入力し、確認します。
# 検証データを説明変数(X_val)と目的変数(y_val)に分ける
X_val = df_val[['weekday', 'High', 'Low', 'Open', 'Close', 'Close_ratio', 'Body']]
y_val = df_val['Up']
# 検証データの説明変数と目的変数を確認
print(X_val)
print(y_val)
学習データと検証データの時系列グラフを作成し2021年前後でデータが分かれていることを目で確認します。2021年以前が学習データで青いグラフ、2021年以降が検証データでオレンジのグラフで示されている事が分かります。
# 学習データと検証データの終値(Close)の折れ線グラフ作成
X_train['Close'].plot(kind='line')
X_val['Close'].plot(kind='line')
# グラフの凡例を設定
plt.legend(['X_train', 'X_val'])
# グラフの表示
plt.show()
・データを整える
予測モデルに学習をさせるために、データを整えます。
説明変数は各週毎の月曜日から木曜日の4日間をセットとして一つにまとめます。また、目的変数は翌日の金曜日の始値が上がるか下がるかを示す木曜日のデータを抜き出します。機械学習を行うためには説明変数と目的変数の数を揃える必要があります。
データの大きさや変動幅が大きく異なっている場合、機械学習では予測が正しく行えない事があります。このような場合に標準化という処理を行います。
この4日毎にデータを抜き出して、標準化を行うための処理を、sklearnのpreprocessingというライブラリのStandardScalerという関数を使って、for文の繰り返し処理を用いて次のような関数を定義します。
また今回、機械学習に使用する予測モデルはLSTMというニューラルネットのモデルを使用します。このモデルではnumpy配列という形式のデータを用います。
#予測モデルに学習させるために、データを整えます
# 標準化関数(StandardScaler)のインポート
from sklearn.preprocessing import StandardScaler
# numpyのインポート
import numpy as np
# 4日ごとにデータを抜き出して、標準化ととnumpy配列に変換する関数(std_to_np)の定義
def std_to_np(df):
df_list = []
df = np.array(df)
for i in range(0, len(df) - 3, 4):
df_s = df[i:i+4]
scl = StandardScaler()
df_std = scl.fit_transform(df_s)
df_list.append(df_std)
return np.array(df_list)この関数をX_trainとX_valに適用してデータの型を確認します。
# 学習データと検証データの説明変数に関数(std_to_np)を実行
X_train_np_array = std_to_np(X_train)
X_val_np_array = std_to_np(X_val)
# 学習データと検証データの形の確認
print(X_train_np_array.shape)
print(X_val_np_array.shape)出力結果>>>
(776, 4, 7)
(94, 4, 7)出力結果から776と94は1/4のデータ個数、4は月曜日から木曜日までの木曜日までの4日分のデータを表しており、7は説明変数のカラム数を表しています。
続いて、目的変数の木曜日のデータだけ抜き出します。抜き出す前に一旦、学習データと検証データのデータを確認します。
#学習データと検証データの確認
# 学習データと検証データの目的変数を確認
print(y_train)
print(y_val)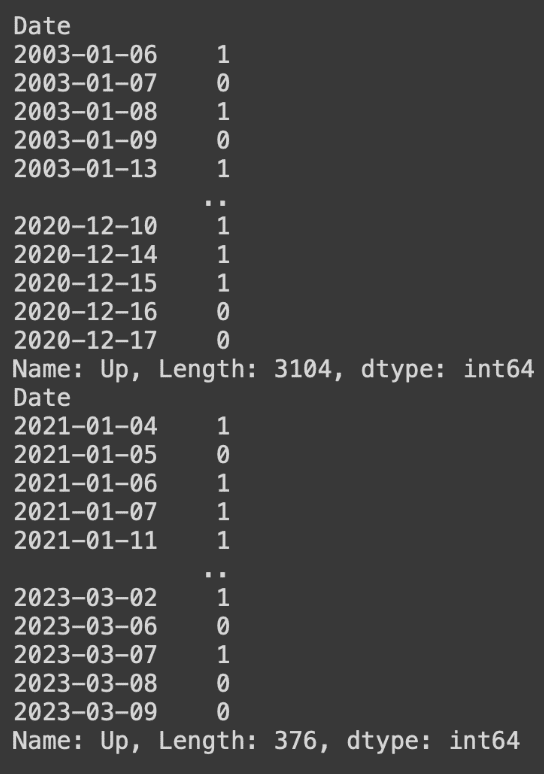
これらのデータに対して、各週の4日目(木曜日)のデータを抜き出して確認します。
# 学習データ、検証データの目的変数の間引き
# 週の4日目(木曜日)のデータだけ抜き出す
y_train_new = y_train[3::4]
y_val_new = y_val[3::4]
# 間引き後の学習データと検証データの目的変数を確認
print(y_train_new)
print(y_val_new)
これで、機械学習を行うためのデータは整いました。
・予測モデルの作成
LSTMを用いて予測モデルの作成と、検証データを用いた予測精度の検証をします。
LSTMを使用するためにkerasのライブラリを使えるようにする必要があります。まずこのためにtensorflowをインストールします。
#kerasから必要な関数のインポート
# keras.modelsからSequentialのインポート
from keras.models import Sequential
# keras.layersからDense、LSTMのインポート
from keras.layers import Dense, LSTM
# Dropoutのインポート
from keras.layers import Dropout次に、モデルの構築をします。
# LSTM構築とコンパイル関数
def lstm_comp(df):
# 入力層/中間層/出力層のネットワークを構築
model = Sequential()
model.add(LSTM(256, activation='relu', batch_input_shape=(None, df.shape[1], df.shape[2])))
model.add(Dropout(0.2))
model.add(Dense(256, activation='relu'))
model.add(Dropout(0.2))
model.add(Dense(1, activation='sigmoid'))
# ネットワークのコンパイル
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
return model次に、作成したモデルが本当に予測に使用できるか確認する方法として、交差検証を行います。今回のような時系列のデータで過去のデータを用いて予測する場合、時系列交差検証を用いるのが一般的です。
時系列交差検証のイメージ写真まず、時系列分割交差検証を行うためのTimeSeriesSplitと、予測結果の精度(accuracy)を算出するためにaccuracy_scoreをインポートします。
# 時系列分割のためTimeSeriesSplitのインポート
from sklearn.model_selection import TimeSeriesSplit
# accuracy算出のためaccuracy_scoreのインポート
from sklearn.metrics import accuracy_scoreつぎに、4回分の交差検証の結果を代入する空のリストを作成します。そして、TimeSeriesSplitのインスタンス化を行い変数(tscv)に代入します。
valid_scores = []
tscv = TimeSeriesSplit(n_splits=4)次に、for文を用いて、交差検証を4回繰り返します。
#for文を用いて、交差検証を4回繰り返します。
for fold, (train_indices, valid_indices) in enumerate(tscv.split(X_train_np_array)):
X_train, X_valid = X_train_np_array[train_indices], X_train_np_array[valid_indices]
y_train, y_valid = y_train_new[train_indices], y_train_new[valid_indices]
# LSTM構築とコンパイル関数にX_trainを渡し、変数modelに代入
model = lstm_comp(X_train)
# モデル学習
model.fit(X_train, y_train, epochs=10, batch_size=64)
# 予測
y_valid_pred = model.predict(X_valid)
# 予測結果の2値化
y_valid_pred = np.where(y_valid_pred < 0.5, 0, 1)
# 予測精度の算出と表示
score = accuracy_score(y_valid, y_valid_pred)
print(f'fold {fold} MAE: {score}')
# 予測精度スコアをリストに格納
valid_scores.append(score)4回の交差検証が終了したら、予測精度のスコアが格納されたリストの表示し、スコアの平均値の算出と表示もしてみましょう。
4回のそれぞれのスコアと、平均値はこのようになりました。
#4回のそれぞれのスコアと、平均値を表示
print(f'valid_scores: {valid_scores}')
cv_score = np.mean(valid_scores)
print(f'CV score: {cv_score}')出力結果>>>
valid_scores: [0.47096774193548385, 0.49032258064516127, 0.45806451612903226, 0.4774193548387097]
CV score: 0.4741935483870967次に、このモデルに対して、2003年から2020年の学習データを用いて学習をします。
# LSTM構築とコンパイル関数にX_train_np_arrayを渡し、変数modelに代入
model = lstm_comp(X_train_np_array)
# モデルの学習の実行
result = model.fit(X_train_np_array, y_train_new, epochs=10, batch_size=64)学習したモデルを用いて、検証データについて予測を行い、先頭の10個を表示します。
# 作成したモデルより検証データを用いて予測を行う
pred = model.predict(X_val_np_array)
pred[:10]出力結果>>>
array([[0.4819296 ],
[0.47399437],
[0.43371078],
[0.4320345 ],
[0.5142206 ],
[0.49131423],
[0.47573858],
[0.47979316],
[0.4444265 ],
[0.45044333]], dtype=float32)この数値を、上がるか下がるかの0と1に変換します。numpyのwhereメソッドを用いて0.5を超えるものを1、それ以外を0と修正します。そして再度先頭の10個を表示します。
# 予測結果を0もしくは1に修正(0.5を境にして、1に近いほど株価が上昇、0に近いほど株価が上昇しない)
pred = np.where(pred < 0.5, 0, 1)
# 修正した予測結果の先頭10件を確認
pred[:10]出力結果>>>
array([[0],
[0],
[0],
[0],
[1],
[0],
[0],
[0],
[0],
[0]])次に、予測モデルの精度確認を行います。この予測結果を実際の値となる検証データの目的変数と比較し、正解率を計算します。sklearnのaccuracy_scoreという関数を使うことで計算が行えます。
この結果を表示すると58%の正解率で有ることがわかります。今回の様な株価が上がるか下がるかの2値の予測では、直感的に予測を行う場合50%の正解率となります。機械学習を用いる事でそれを超える正解率となりました。
# 実際の結果から予測値の正解率を計算する
from sklearn.metrics import accuracy_score
print('accuracy = ', accuracy_score(y_true=y_val_new, y_pred=pred))出力結果>>>
accuracy = 0.585106382最後に、予測結果と正解結果を混同行列を用いて確認します。
混同行列とは、このように2行2列の表で、真陽性、真陰性、偽陽性、偽陰性の数を表したものです。今回は、予測が0で結果も0、予測が1で結果も1であれば正解です。0と予測して結果が1、1と予測して結果が0なら不正解ということになります。全体の精度だけではなく、0と1それぞれの正解に対する精度を確認することができます。
混同行列を生成するために、sklern.mericsからconfusion_matrixとConfusionMatrixDisplayをインポートします。
また、視覚的にわかりやすい様に、ヒートマップで表示しましょう。
このように、正しく予測が行えているのは、右下の真陽性(TP)と左上の真陰性(TN)です。予測結果が、0か1のどちらかに極端に偏っている傾向ではなさそうですが、正しく予測できていないものも存在していることがわかります。予測精度を改善することで、偽陽性(FP)と偽陰性(FN)の数を減らすことができます。
# 混同行列生成のためconfusion_matrixをインポート
from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplay
# 混同行列を表示
cm = confusion_matrix(y_val_new, pred)
cmp = ConfusionMatrixDisplay(cm)
cmp.plot(cmap=plt.cm.Reds)
混同行列から、左上は正解ラベルが0で予測値も0となっているのでうまく予測できていることがわかります。
対して、右上は正解ラベルが0で予測値が1となっておりますので、うまく予測できていないことがわかります。
上記から、うまく学習できておらず、精度を高めるために全て0と予測していることがわかりました。
最後に
正解率が58%という結果となりました。
今回、特徴量として、株価の変動に影響すると言われている一般的な情報(特徴量)である『終値の前日比率と、始値と終値の差分』を追加してみました。
また、モデルのパラメーターの調整や、特徴量を追加することで、さらに予測精度が上がる可能性があることがわかりました。
株価の予測は不確実要素が多く、完全に予測できないものであるため、参考程度に見ていただけたら嬉しいです。
