
ビザンチン将軍問題がおもしろい。
最近、キングダムを見ているじん。展開として、将軍たちが仲間同士争うことや誰かが裏切ることによって、勝敗が決まることが多いです。数学界やブロックチェーンでも分散型という形をとると同じようなことが起きます。
少しその「裏切り」の問題に足を突っ込んでみましょう。
↓↓↓目次↓↓↓
ビザンチン将軍問題とは?
ビザンチン将軍問題は、分散システムにおける信頼性の問題を説明するために、1982年にレスリー・ランポート博士らによって提案された古典的なコンピュータサイエンスの課題のこと。この問題は、複数の参加者(ノード)が協調して行動しなければならない状況で、一部の参加者が故意に不正確な情報を提供する可能性がある場合に、全体として正しい合意を形成できるかどうかを問うものです。
ビザンチン将軍問題のシナリオ: 侵攻か撤退か
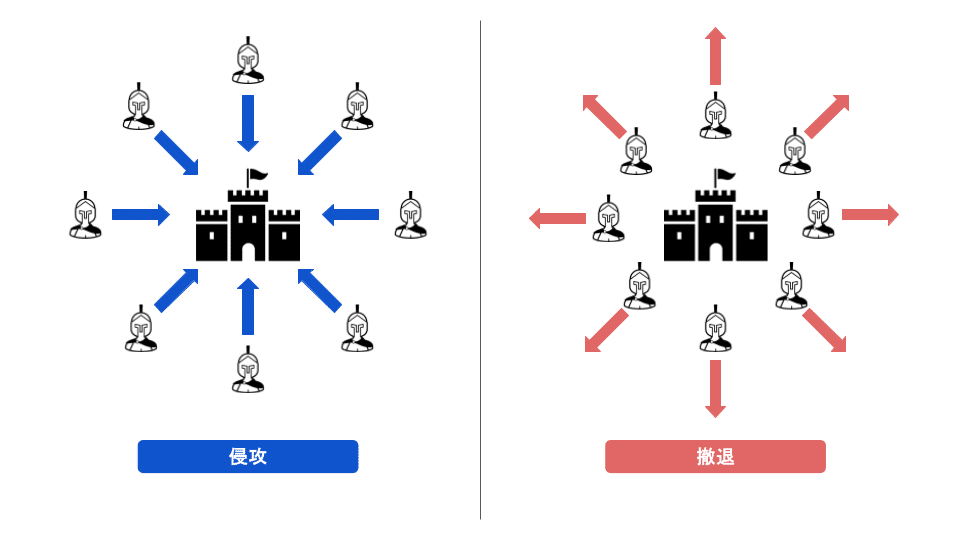
ビザンチン帝国の将軍たちは、ある敵の都市を包囲しています。このとき、全員が一致して侵攻するか、全員が一致して撤退するかを決めなければなりません。なぜなら、一部の将軍が侵攻を決断し、他の将軍が撤退を決断すると、軍が分裂してしまい、総合的に見て損になってしまうリスクがあるからです。
ただし、将軍たちはそれぞれ異なる場所におり、直接話し合うことができません。代わりに、使者を通じてメッセージをやり取りします。この時に発生する問題として、このメッセージのやり取りの中で、裏切り者がいる可能性があるということです。裏切り者は、他の将軍たちが一致した行動を取れないように、誤った情報を伝えられる状況にあります。
この前提のもとで、全員が一致した行動を取れるかどうかが問われるのがビザンチン将軍問題です。以下では、各将軍が裏切り者だった場合に、どのように合意形成が妨げられるかを具体的に見ていきます。3人が最小単位となり、本来は複数人がいるため数学的にはN人として考えてみる必要があります。

この状況が、分散システムにおけるノード間の通信や合意形成において、信頼性を維持することの難しさを象徴しています。
ビザンチン将軍問題における数学的な条件
ビザンチン将軍問題を解決するための重要な条件として、
裏切り者の将軍が N 人存在する場合、
誠実な将軍が 2N + 1 人以上であれば、
誠実な将軍同士の意見が一致する可能性が高くなります。
ことが知られています。この条件について、以下に数学的に説明します。
問題設定
将軍の総数を T とします。
裏切り者の数を N とします。
誠実な将軍の数を T-N とします。
合意の条件
合意形成のためには、誠実な将軍の意見が一致する必要があります。誠実な将軍の意見が一致するためには、誠実な将軍の数が裏切り者の影響を受けないだけの多数派であることが必要です。
例え話として、将軍が3人いたとしましょう。そのうちの誰か1人が裏切ると仮定します。そして、伝達の順番は A → B → C です。それぞれの将軍が裏切った場合にどのような影響が出るか見てみましょう。
ケース1: A が裏切った場合
A が B に間違った情報を伝えます。B はその情報を C に伝えますが、C は B からの情報しか得られないため、A の裏切りに気づけません。この場合、B と C の間で誤った判断が共有される可能性が高く、正しい合意が形成できません。
ケース2: B が裏切った場合
A は正しい情報を B に伝えますが、B がその情報を改ざんして C に伝えます。この場合、C は A の意図と異なる情報を受け取り、判断が誤る可能性があります。ここでも、正しい合意が難しくなります。
ケース3: C が裏切った場合
C は最終的に決定を下す役割を持ちますが、B から得た情報に基づいて裏切り行為を行います。この場合、C の誤った判断が全体の合意を乱すことになります。特に A と B が正しい情報を共有していても、C の裏切りによって最終的な決定が誤る可能性があります。
これらのケースからわかるように、1人の裏切り者がいるだけで、残りの誠実な将軍が正しい合意を形成することが難しくなることが理解できます。この問題を防ぐためには、誠実な将軍の数が十分に多く、裏切り者の影響を排除できるだけの信頼性が必要です。
不一致の影響
上記のように、誠実な将軍が2人しかいない場合、裏切り者が1人いるだけで、その裏切り者が2人の誠実な将軍に異なるメッセージを送ることで、誠実な将軍同士の意見を分裂させることができます。もし、N人いる場合には、誠実な将軍が少なくとも 2N + 1 人以上いる必要があります。
2N + 1 人の必要性
誠実な将軍が 2N + 1 人以上いると、裏切り者がどのようなメッセージを送ろうとも、誠実な将軍の意見が一致する可能性が高くなります。具体的には、各誠実な将軍は他の将軍からメッセージを受け取りますが、少なくとも 2N + 1 人の誠実な将軍から受け取るメッセージが一致していれば、裏切り者が何をしようと、その意見に従わずに正しい結論を得ることができます。
3N + 1 の条件
誠実な将軍が 2N + 1 人以上いる場合、全体の将軍の数 T は 3N + 1 人以上である必要があります。つまり、誠実な将軍が 2N + 1 人以上、裏切り者が N 人存在するので、全体の将軍の数は T = 2N + 1 + N = 3N + 1人以上でなければならないということです。
ブロックチェーン技術における信頼性の課題
課題
ビザンチン将軍問題は、ブロックチェーン技術において非常に重要な概念です。分散型のシステムでは、ノードがネットワーク全体で協調して動作する必要がありますが、一部のノードが故障したり、不正を行う可能性がないとは言い切れません。むしろ、ある可能性の方が高いとも言えます。そういった状況でも、システム全体が正しく機能し続けるためには、信頼性の高い合意形成(コンセンサス)が必要です。
コンセンサスアルゴリズムによる解決
ビザンチン将軍問題を解決するために、ブロックチェーン技術では"コンセンサスアルゴリズム"が使用されます。代表的なアルゴリズムには、ビットコインで使用されているProof of Work (PoW) やイーサアルゴリズムで使用されているProof of Stake (PoS) があります。これらは、分散型のネットワーク(P2Pネットワーク)内での合意形成を可能にし、特定の中央管理者が存在しない環境でも信頼性のある取引を実現できるようになっています。
Proof of Work (PoW):
計算力を用いてブロックを生成し、ネットワーク全体での合意を形成します。ビットコインはこのPoWを採用しており、正当にマイニングを行って報酬を得る方が、不正を働くよりも効率が良いという環境を作り出すことで、ビザンチン将軍問題を解決しています。Proof of Stake (PoS):
ノードの保有する資産量に基づいてブロック生成の権利を与える方法です。これにより、エネルギー消費を抑えつつ、ネットワークの合意形成を行います。ステーキングによってネットワークへの誠実さを示し、不正行為が発覚した場合には資産が没収されるか、ブロックチェーン・トークンの信頼性が損なわれるため、資産の価値が毀損します。このため、不正行為を避ける方が賢明であるという仕組みです。
コンセンサスアルゴリズムについては以下のnote記事をご参照ください!
