Pythonで学ぶ暗号技術② 楕円曲線暗号を実装してみよう！

こんにちは。学びの探求者です。

前回の記事では、RSA暗号と楕円曲線暗号の違いを学びました。

RSA暗号は「素因数分解が難しい」という数学的性質に基づく一方で、楕円曲線暗号は「楕円曲線上の逆算が難しい」という性質を利用していることを紹介しました。

今回は、楕円曲線暗号がなぜ安全なのか？ をより深く理解し、Pythonを使って実際に暗号化・復号を実装してみましょう！

1. 楕円曲線暗号を安全にしている仕組み

楕円曲線暗号が安全なのは？

RSA暗号では、公開鍵 n = p × q の p, q を素因数分解するのが難しいため、セキュリティが成り立っています。

一方、楕円曲線暗号では、「k × P の計算は簡単だけど、逆に k を求めるのは難しい」 という性質を利用しています。

楕円曲線上の演算（点の加法・スカラー倍算）

まず、楕円曲線とは、以下のような方程式で表される曲線です。

y^2=x^3+1（簡単なもので表現してます）

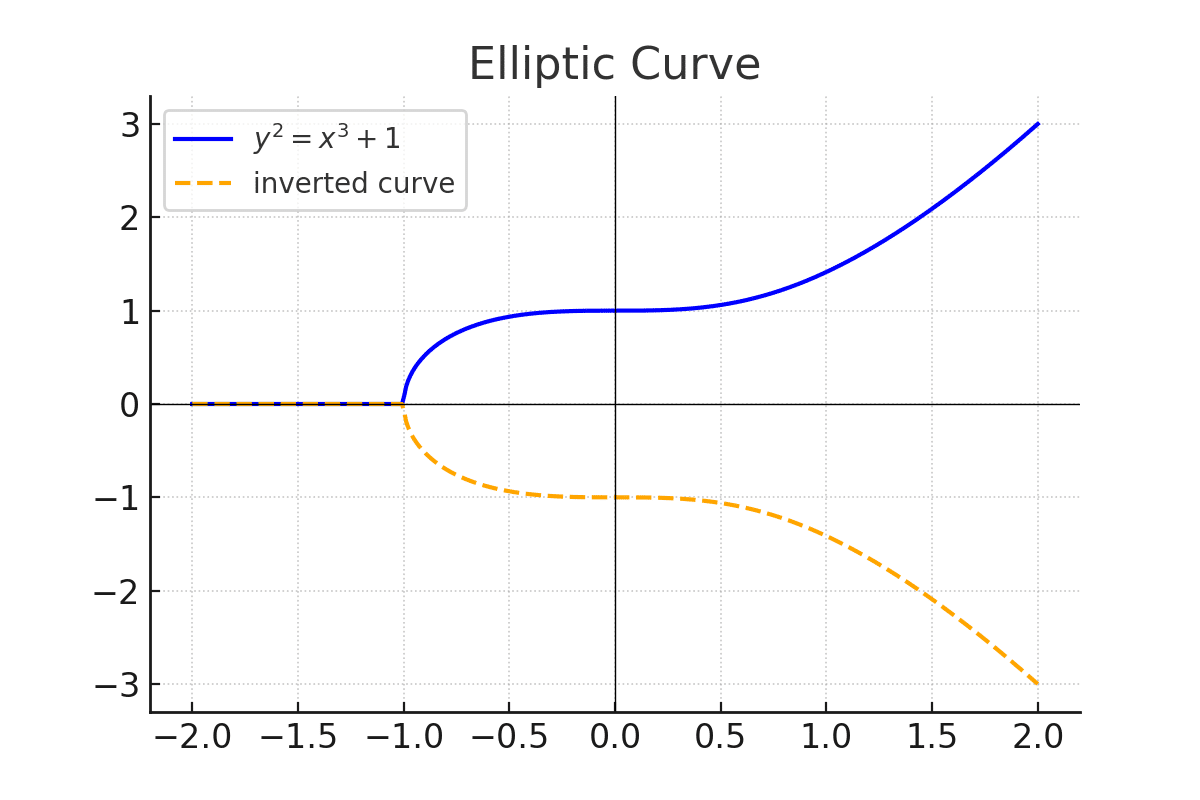
この曲線上で特定の演算を行うことで暗号技術に応用できます。

1.点の加法（P + Q = R）

楕円曲線暗号では、「点の加法」という特殊な演算を使います。

1. 2つの点（P1, P2）を選ぶ（図の赤い点）

2. P1とP2を結ぶ直線を引く

3. その直線と楕円曲線が交わる点（R'）を見つける

4. R' を x 軸に対して反転した点（R）を、新しい点 P1 + P2 とする

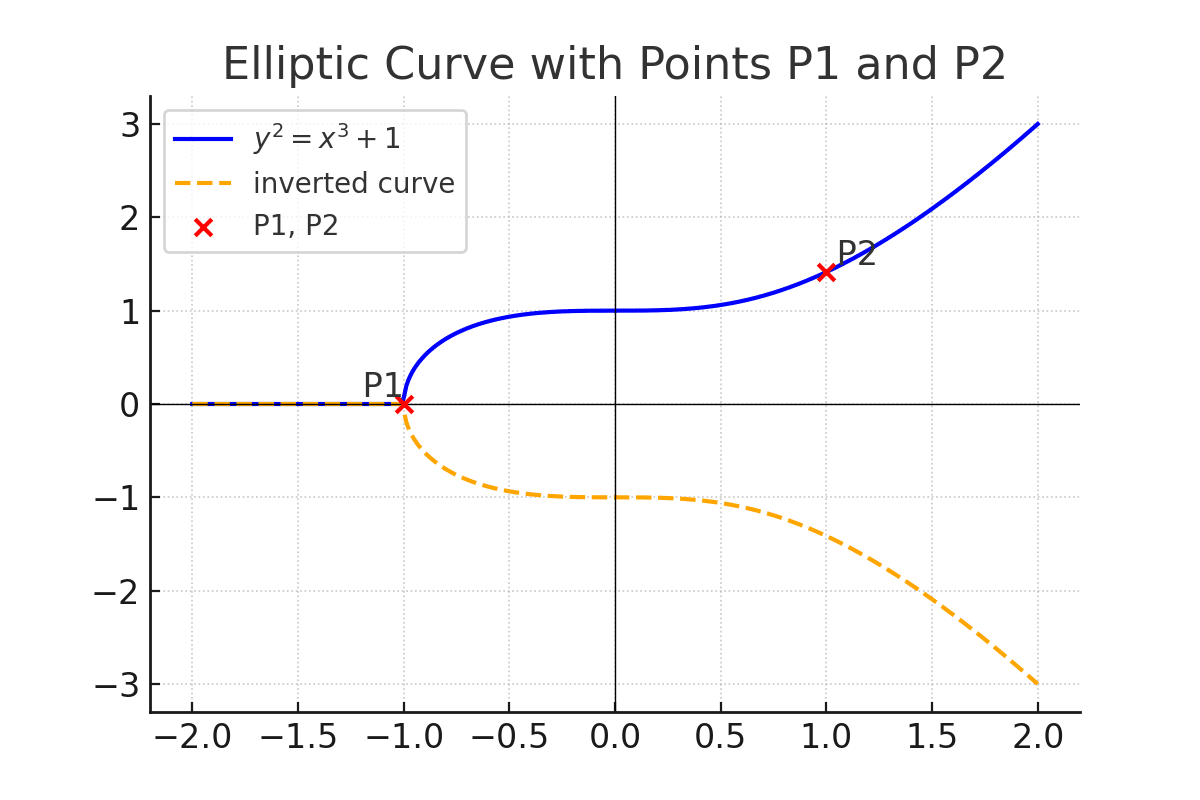
2.スカラー倍算（k × P）

次に、「同じ点 P を何度も足していく」 という操作を考えます。

1. 「2P = P + P」 を計算する → P から楕円曲線に接線を引く

2. 「3P = 2P + P」 を計算する → 2P と P を結ぶ直線を引く

3. 「4P = 3P + P」 を計算する → 3P と P を結ぶ直線を引く

離散対数問題とは

上記のように、P から 2P, 3P, 4P を求めるのは簡単です。
しかし、逆に「P から何回足せば kP になるか？」を求めるのは、難しい。
このことを専門的な用語で 離散対数問題 と呼び、楕円曲線暗号 の安全性の基盤になっています。

2. 安全な通信のカギを握る「共通鍵」

楕円曲線暗号（ECC）は、RSAとは異なり、共通鍵を安全に共有することが前提となっています。これは、ECDH（Elliptic Curve Diffie-Hellman） という仕組みによって実現されます。

ECCの安全性は、「離散対数問題が難しい」 ことに加え、「共通鍵がなければ安全な通信が成り立たない」という仕組みによるものです。

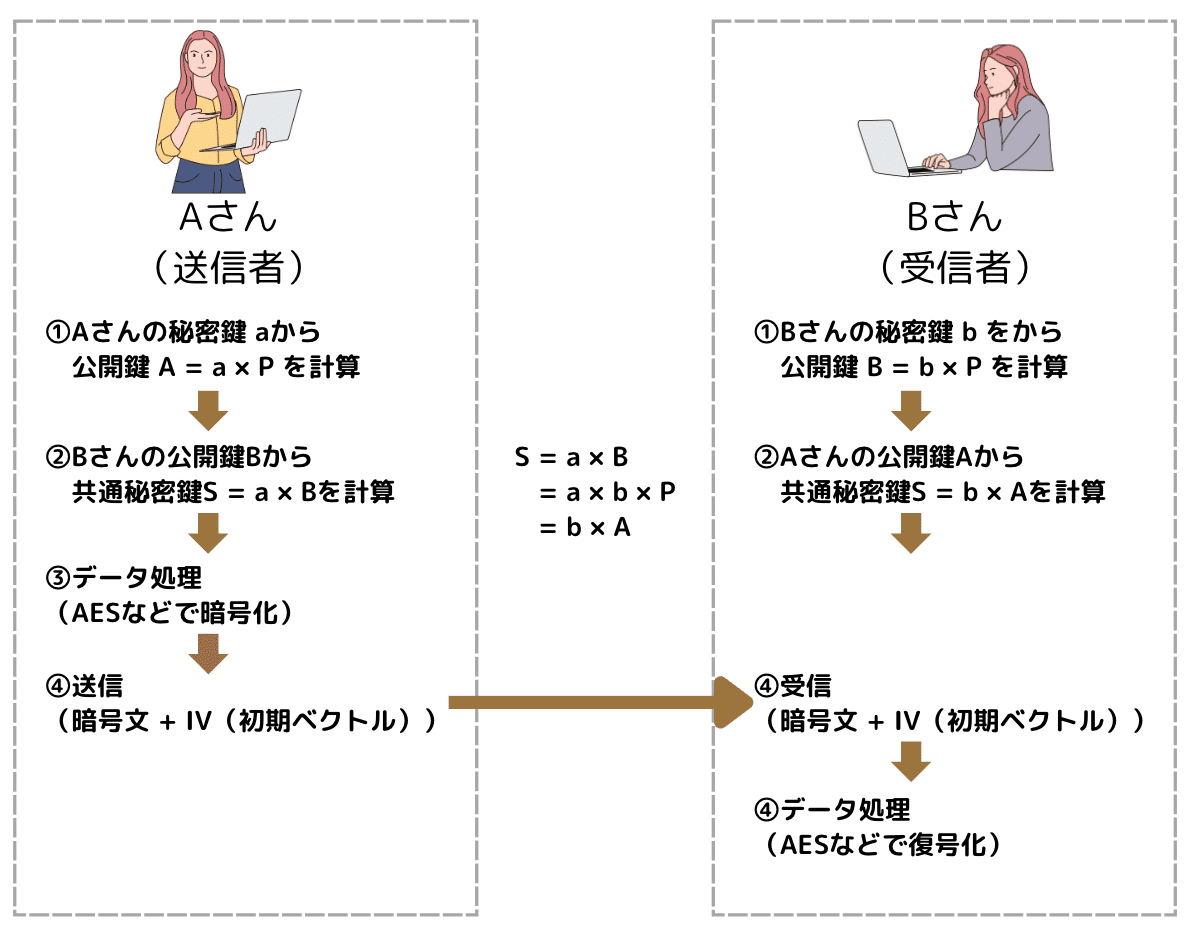
例えば、Aさん（送信者）とBさん（受信者）が安全なメッセージをやりとりする場合、次のような流れになります：

1. Bさんが秘密鍵を作成し、公開鍵をAさんに送る。

2. AさんはBさんの公開鍵を使って、秘密のメッセージを暗号化する。

3. Bさんだけが持つ秘密鍵で、メッセージを復号する。

このように、公開鍵で暗号化し、秘密鍵で復号する というプロセスを確立することで、安全なデータ共有が可能になります。

共通秘密鍵を使った図

3. 実際に、暗号化して復号化してみる

では、Pythonを使って、楕円曲線暗号を用いた暗号化と復号を実装してみましょう！

Pythonで秘密鍵・公開鍵を生成

まずは、Pythonの cryptography ライブラリを使って、AさんとBさんの秘密鍵・公開鍵を作成 します。

コード

from cryptography.hazmat.primitives.asymmetric import ec

# Aさんの鍵ペア
private_key_A = ec.generate_private_key(ec.SECP256R1())  # 秘密鍵
public_key_A = private_key_A.public_key()  # 公開鍵

# Bさんの鍵ペア
private_key_B = ec.generate_private_key(ec.SECP256R1())  # 秘密鍵
public_key_B = private_key_B.public_key()  # 公開鍵

共通鍵を作る

次に、鍵交換（ECDH）を使い、AさんとBさんが共通鍵 S を計算 します。

コード

# Aさんが共通鍵を計算
shared_secret_A = private_key_A.exchange(ec.ECDH(), public_key_B)

# Bさんが共通鍵を計算（Aさんと同じ結果になる）
shared_secret_B = private_key_B.exchange(ec.ECDH(), public_key_A)

# 確認（両者の共通鍵が一致する）
assert shared_secret_A == shared_secret_B  # True ならOK

暗号化・復号化

共通鍵はそのまま使わず、AES鍵を派生（HKDF を使用） し、AES-GCMで暗号化・復号化します。

コード

import os
from cryptography.hazmat.primitives.kdf.hkdf import HKDF
from cryptography.hazmat.primitives import hashes
from cryptography.hazmat.primitives.ciphers import Cipher, algorithms, modes

# 鍵派生関数（HKDF）を使い、共通鍵から AES 用の鍵を生成
def derive_key(shared_secret):
    return HKDF(
        algorithm=hashes.SHA256(),
        length=32,
        salt=None,
        info=b"ECC Key Agreement",
    ).derive(shared_secret)

# AさんとBさんの AES 鍵を作成（同じ鍵になる）
aes_key_A = derive_key(shared_secret_A)
aes_key_B = derive_key(shared_secret_B)

# AES-GCM で暗号化
def encrypt(message, key):
    iv = os.urandom(12)  # 初期ベクトル（IV）
    cipher = Cipher(algorithms.AES(key), modes.GCM(iv))
    encryptor = cipher.encryptor()
    ciphertext = encryptor.update(message) + encryptor.finalize()
    return iv, ciphertext, encryptor.tag

# AES-GCM で復号化
def decrypt(iv, ciphertext, tag, key):
    cipher = Cipher(algorithms.AES(key), modes.GCM(iv, tag))
    decryptor = cipher.decryptor()
    return decryptor.update(ciphertext) + decryptor.finalize()

# Aさんがメッセージを暗号化
message = b"Hello, ECC encryption!"
iv, ciphertext, tag = encrypt(message, aes_key_A)

# Bさんが受信し、復号化
decrypted_message = decrypt(iv, ciphertext, tag, aes_key_B)

# 確認（復号後のメッセージが元と同じならOK）
assert decrypted_message == message  # True なら成功
print("復号メッセージ:", decrypted_message.decode())

結果

復号メッセージ: Hello, ECC encryption!

まとめ

いかがでしたか？
今回は、楕円曲線暗号を使った安全な通信の仕組みを学びました。
前回に引き続き、少し数学的な話が多かったかもしれませんが、日常のセキュリティがこうした技術に支えられていると考えると、面白く感じられるのではないでしょうか？
少しでも興味を持っていただけたら嬉しいです！

---

最後まで読んでくださりありがとうございます。
また少しでも読んでみたいな、ぜひ「いいね」や「フォロー」で応援してくれると嬉しいです！💡✨