
【モーションキャプチャ】計測原理と三角測量の話
★この記事で分かること★
モーションキャプチャの計測原理
三角測量の理論、算出方法
★こんな人に読んでほしい★
数学や物理がどのようなことにに役立っているのか知りたい方
ある程度の数学を習熟している学生の方
★読み終わるまでの目安時間★
10分
ロジマジBlogへようこそ!モーションキャプチャ担当のいっしーです!
先日、深夜3時ごろに外からにぎやかなお囃子が聞こえてきてオバケが迎えに来たのかと思ったら、近所の神社の宮出しでした。怖かったです。
さて、今回の記事は少々趣向を変えまして、モーションキャプチャ×数学という記事になっております。
モーションキャプチャでなぜ三次元座標が得られるのか、その原理や直感的理解のための三角測量の話をしようと思います!
高校数学までの知識さえあれば理解できる記事になっていますので、モーキャプ専門外の方もぜひご覧ください!
モーションキャプチャの仕組み
光学式モーションキャプチャではマーカーの三次元座標を捉えることで、人や物の動きを計測します。
では、なぜマーカーの三次元座標が分かるのでしょうか。
その仕組みを簡単に紹介します。
~再帰性反射~
まず1つはマーカーが持つ「再帰性反射」という性質です。

再帰性反射のイメージはこんな感じです。
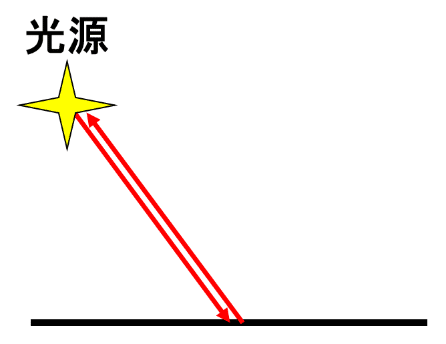
光源から放たれた光が反射面に当たった後に、光源方向のみに戻るように反射します。
すると反射した光が拡散することなく、その光を効率良く捉えることができます。
再帰性反射の性質を持つ素材は、視認性が求められる道路標識や安全服、ペットの首輪などに使われています。
余談ですが、「光の反射」は定義として「拡散反射(乱反射)」「鏡面反射(正反射)」「再帰性反射」の3種類に分類されます。
「拡散反射・乱反射」のイメージは下図です。
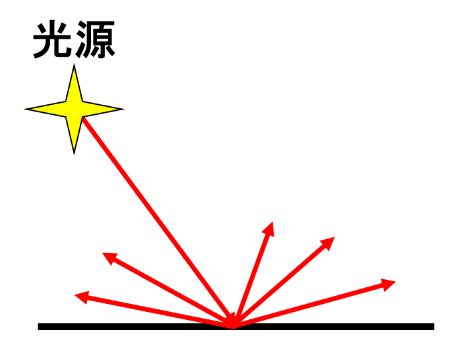
光源から出た光が反射面に当たった後、あらゆる方向に反射します。
光源方向にも光は帰ってきますが、拡散されるためその光量は少なくなるため、視認性は低くなります。
一般的に表面の粗い物質や光沢・艶の無い物質に多く見られる反射です。
次に、「鏡面反射・正反射」のイメージは下図です。
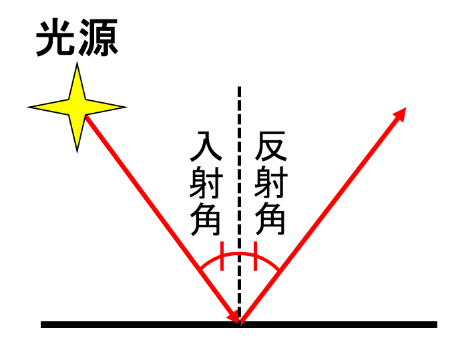
光源から出た光が反射面に当たった後に、入射角と反射角が等しくなるように反射します。
一般的に鏡や光沢・艶のある物質に多く見られる反射です。
この反射は光源方向に戻らないというだけで反射した光は拡散しません。
したがってスタジオ内にこういった素材があるとマーカーと誤認識してしまうことがあります。
上記2種類の反射をまとめて「全反射」と呼びます。
~キャリブレーション~
1台のカメラでは2次元座標は分かるものの距離や奥行の情報が分かりません。

そこで2台以上のカメラでマーカーを撮影することでその三次元位置を計算することができます。
そのためにカメラの位置や角度、原点や座標軸を定義するキャリブレーションという作業を行います。
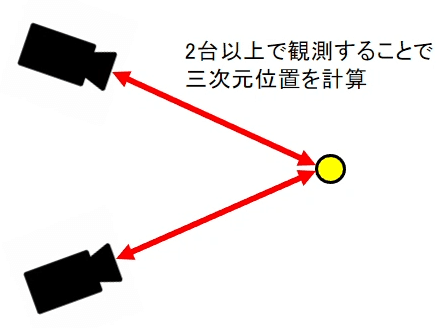
このキャリブレーションについては別記事で詳しく説明します!
キャリブレーションで定められたカメラ位置、角度などからマーカーの三次元位置を計算します。
一般的な光学式モーキャプではエピポーラ幾何という原理によってマーカーの三次元化が行われますが、Viconではサークルフィッティング法という独自のアルゴリズムを用いているそうです。
三角測量
エピポーラ幾何を理解するためには幾何学や線形代数といった大学数学でも限られた人しか習わない知識が必要なので、少々取っ掛かりにくいかと思います。
そこで今回は高校数学の範囲でも理解できる三角測量について紹介します。
エピポーラ幾何と比較すると非常にシンプルな手法ではありますが、2つの地点から観測することで奥行き情報が得られるという直感的な理解ができると思います!
下の図のように対岸にある木を女の子と男の子が観察している場面を考えましょう。

女の子と男の子の距離をL、各々の木までの目線と川がなす角をそれぞれαとβ、そして木から対岸までの距離をdとします。

このとき、Lとαとβは既知、dは未知となります。
それではここからdを求めていきましょう。
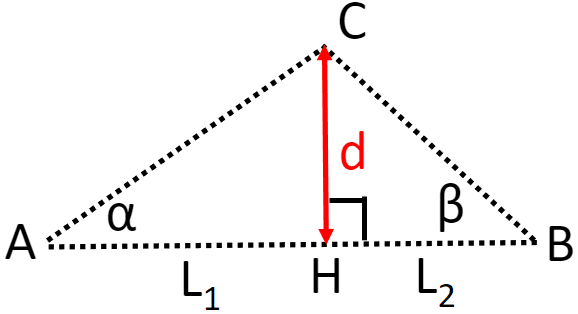
見やすくするために簡略化した下図で考えていきます。
まず点A,B,Cをおき、点Cから辺ABに対して引いた垂線とその交点を点Hとし、AHをL1、BHをL2とします。
△ACHにおいて三角関数を用いると
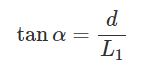
すなわち
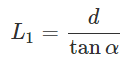
となります。
同様に△BCHにおいて
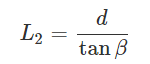
となります。ここで
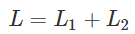
であることと先ほど求めたL1とL2から
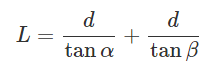
という式が得られます。
この時点で変数がdのみなので、式を整理して美しくしましょう。
まずは右辺に注目し、共通因数dで括ります。
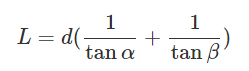
左辺にdが来るように式変形をします。
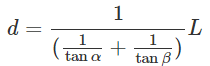
*三角関数の相互関係を用いて右辺を変形します。
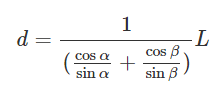
* tanθ=sinθ/cosθ
引き続き右辺に注目し、分母の分数を通分してまとめます。
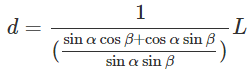
*単純連分数であることから下のように変形できます。
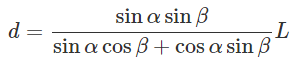
*分子が1である連分数(分母が分数である分数)
1/(b/a)=a/b
最後に、分母に*加法定理を用いてこのようになります!
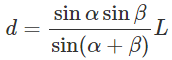
*sin(α±β)=sinα cosβ ± cosα sinβ
cos(α±β)=cosα cosβ ∓ sinα sinβ
実際に求めてみよう
それでは、実際に数字を当てはめて考えてみましょう。
女の子と男の子の距離を10m、各々の木までの目線と川がなす角をそれぞれ30°と45°と仮定します。
これらを用いて対岸の木までの距離をdを求めてみましょう。

先ほど得られた式にα、β、Lに値を代入します。
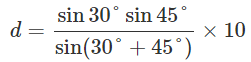
計算を始める前に三角関数を整理しておきましょう。
*単位円を書いてみると
*単位円:原点を中心とした半径が1の円
円の中に斜辺が1となる直角三角形を書くことで
任意の角度に対する正弦、余弦、正接を求めることができる

30°と45°の余弦(cos)、正弦(sin)の値がそれぞれ以下の値だということが分かります。
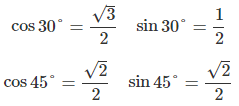
次に分母の計算がやや複雑そうなので先に済ませておきます。
加法定理を用いて
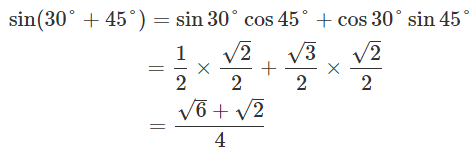
この様に計算できます。この値と三角関数の値を代入します。
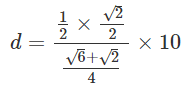
分子を計算します。
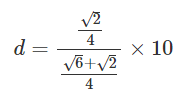
*繁分数の中の分数の分母を払います。
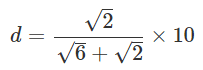
*繁分数:分母または分子または両方に分数が含まれている分数
ここで分母の*有理化を行います。
分子分母に(√6-√2)をかけます。
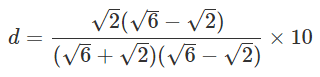
*有理化:根号(√)を含まない形に変形すること
*和と差の積の公式より分母が有理数になります。
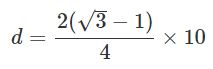
*和と差の積の公式:(a+b)(a-b)=a^2-b^2
そして、式全体を約分します。
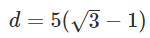
最後に、√3を1.732で近似すると
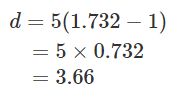
木までの距離がおよそ3.66mだということが分かりました!
念のため計算アプリで確認しましょう。

正解でした!良かったです!
もっと簡単なイメージ
2点の観測点から奥行情報が分かるという事実を
一瞬で!!
理解できる例を最後に書いて終わろうかと思います!
以下のように値が分からない座標をX軸方向とY軸方向に設置したカメラからそれぞれ観測することを考えてみましょう。

X軸方向から観測すると、X座標の情報が失われ、認識できる座標が(〇,2,3)となります。
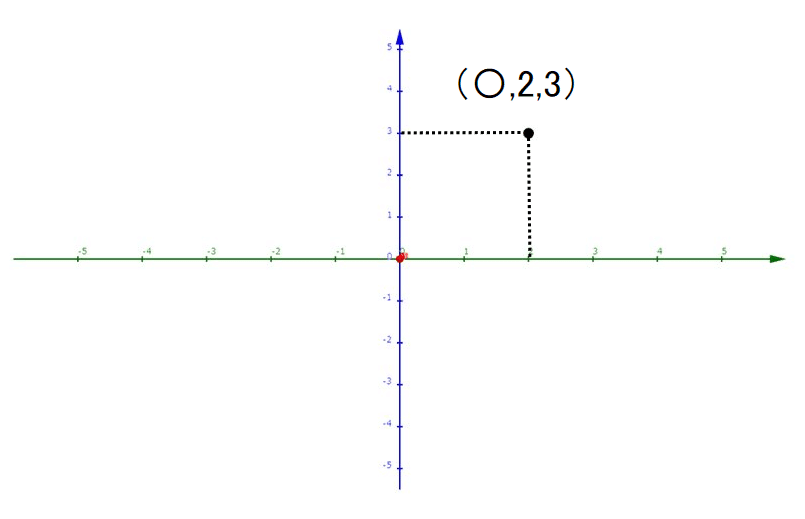
同様にY軸方向から観測すると、認識できる座標が(1,〇,3)となります。

この2方向からの情報を組み合わせることで(1,2,3)という三次元座標が明らかになります。

2点から観測することで三次元座標を求めることができるということが直感的に理解できるかと思います!
最後に
というわけで今回の記事ではモーションキャプチャの原理、三角測量といったお話をさせていただきました。
モーションキャプチャに限った話ではないですが、世の中の多くの技術がこうした数学を土台に成り立っています。
数学というメガネを通して世界を見てみるとまた違った見え方がして楽しいですよ!(私はスマブラをするとベクトルが見えていた時期がありました)
最後までご覧いただきましてありがとうございました!
それでは、また別の記事で!
株式会社LOGIC&MAGIC
モーションキャプチャ担当 いっしー
*******************************
お仕事や見学のご相談:CONTACT
リクルート:RECRUIT
*******************************
