OMC052(4b)参加したよって話

きましたーまさかさくんの単独4bです
強すぎてムカつくので全完したいですね...

A

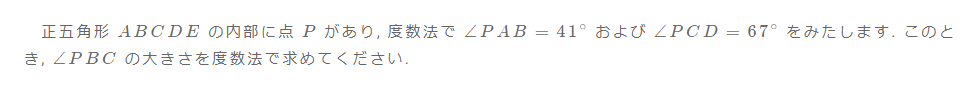
え？？？？100点の難角？？
かと思えば41+67=108でした、早く気付くべきだった...

B

1.1倍するほうが40mlを足すよりも得になるのは、400ml以上の時です。
なので、40mlを10回足してから、1.1倍を5回するんだろうな～と思いました、が...

まさかの電卓の押しミスで2ペナ！w
いやつらいです... 無駄なペナは減らしていきたい....

C

最小でも各面に書かれる数は4!=24なので、面に書かれる数はちょうど2種類であることが分かります。
最初、(8!)^3を分ける... みたいなことを考えましたが、よくよく考えると7を挟む3つと5を挟む3つの2種類にしかなり得なさそうです。
つまり7と5を除いた1,2,3,4,6,8から3つを選んで積が同じになる方法を考えればいいですが、どうせ48やろ！wと勘で行ったら(1,6,8)(2,3,8)(2,4,6)で行けて、わーいになりました...(おい)

このとき、こんな感じ↓で配置すれば条件を満たし、答えは336です！

D

えぐそう....... というのが初見の感想です
最初は5個以下を引くのかな、と思いましたがめんどくさそうな上、6個と7個しかないので、たぶんそのまま求められるんだろうな、と思いました.

7個の場合は簡単で、2021C6通りすべてについて1通りずつあるので、2021C6/2021C5=336です(336って数字好きだな)

6個の場合は少しめんどくさいです...
まず、出てくる頂点が6個の時、2021C6通りすべてについて3通りあります.
また、出てくる頂点が5個の時(コーナーケース危ない)、2021C5通りすべてについて5通りあります.

なので合計336+336×3+5=1349かなぁ、と思って、提出したところ、まさかのノーペナCA！！　かなり正答率が低そうだったので、嬉しいです～

E

なんかOMC051に似たのあったくね？？となりました(が見ませんでした...)
99元連立方程式なのでどうにかしてf(100)を出すのかな、と思いましたが、どうにかが思いつかず、CAできませんでした... うーん
解説を見たところ、なんかすごそうですね...() 頑張って理解します

F

3×2^10を見て、どうせ整数問題に帰着するんだろ、となりました。
ちょっと悩みましたが、とりあえず三平方でやってみます。

まずAC^2=AD^2+9×2^20は分かります。
ところで、AC^2-AE^2 = BC^2-BE^2 = 9×2^20ですね。あれ？
BCとBEは整数なので... 勝った！！

いや簡単ではないですが
(BC+BE)(BC-BE)=9×2^20で、どちらも偶数になるしかないので、結局9×2^18の約数のうち3×2^9より小さいものの総和をだして、2を掛ければいいです。

1×2^nで表せるものは、1×(1+2+...+1024)=2047であり、
3×2^nで表せるものは、3×(1+2+...+256)=1533であり、
9×2^nで表せるものは、9×(1+2+...+128)=2295なので、

電卓ぽちって2を掛けると、答えは11750になりました。
そして提出したところ... またノーペナCA！嬉しいです～

結果

ABCDFの5完で、15位でした！！！ひゃっほう！！！！！！
ペナ数が少なかったのが大きな原因だと思います、嬉しい～
ただ全完できなくて悔しいですね... まさかさ、まじで何者なのか...

さて、次回はまたWolfram Cupです... 恐怖の3-5-5-7-7-7-9で、冷える予感しかしませんが、とりあえず頑張りたいです...！