OMC卬高杯1(有志)参加したよって話
ふおおお!!ついに来ました、有志コンです!!
静岡高校数学同好会の皆さん、よろしくお願いします!
A
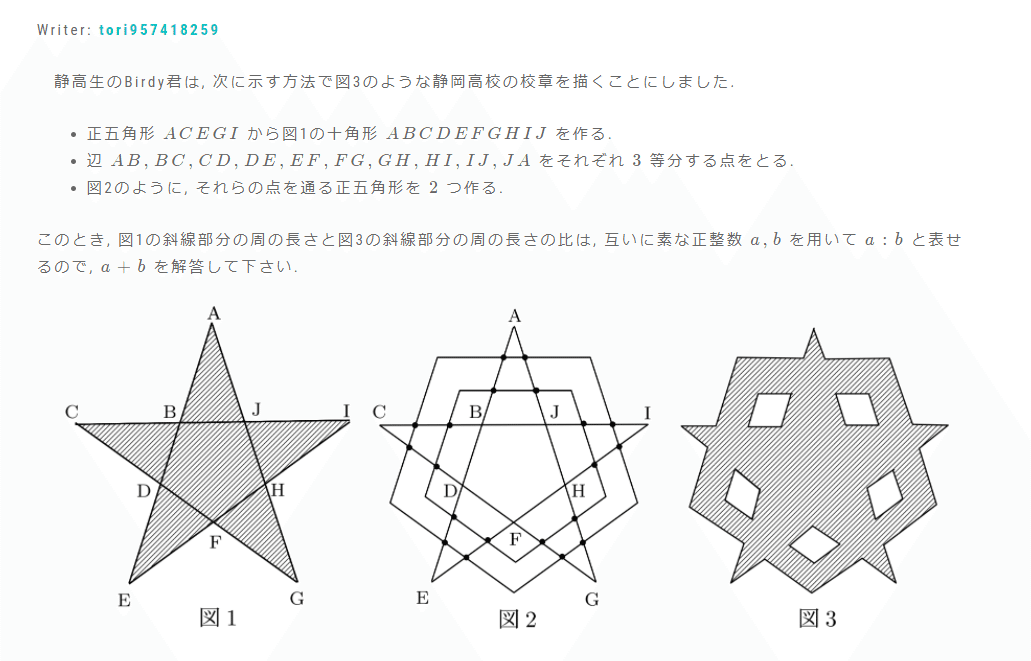
面白いですね... っつか普通にすごいきれいな校章なのだが
ちょっと悩むのですが、BCを3等分した長さを1としたらそれぞれ30と50で、求める答えは8になります。2位で悔しかった...
B

んぎゃー難しそう... ということでCを先に解いてから戻ってきました
(s,t,u)を固定して、それが含まれる組が何個あるかを考えました。
なんかこの考え方って典型っぽいんですかね...(典型だよ精進しろ) 解説に「以下の成立が容易にわかる」って書いてあって、は?笑になりました...
C

これほんまに300点か???となりましたが、よくよく考えたら対称式なので、xyzとxy+yz+zxとx+y+zで連立方程式ができそうです。
しかし、連立方程式の立て方も、xyzとxy+yz+zxとx+y+zの値も間違わなかったのに、なぜか最後の最後の求値でミスり(???)、2ペナしました...
D

解いた問題の中では最後に解いた問題です。
シグマの中の式が変形できるのかな、と思ったのですができず、結局分からないままEに進み、帰ってきました。そしてlocker氏の心に、悪魔が浮かんでしまったのです―
「「「「答え求められたらいいんじゃね?」」」」
3や4などの小さい値で試すと、どうやら(n+1)/2になりそうなので、1011を提出したら、まさかのCA...
解説を見て感動しました、ごめんなさい、もう未証明CAはしたくないです
E

まず問題文を読むのに3分ほどかかりました(おい)
そして読解してからも、え、これ1しかないんでは、とずっと勘違いしていました(今思えばなんでだよってなりますが)
ただ、その時の考え方で、入っているグループ数の偶奇が変わらないことが分かったので、2021Cnが奇数になるnかな?と思います。
そして筆者は思い出します... そう... OMC011-Eを!!

onlinemathcontest.com上の情報は見ても構わないんだし... うん... 別にめんどくさくなったとかそういう訳じゃないし... うんうん...
かれこれして、2021Cnが奇数になる0≤n≤2021が256個あることが分かりました。しかし!筆者は2022の存在を忘れませんでした!
256個に2022を加え、257と解答!!
![]()
ばかなん?0は違うに決まってるやろ、ばかなん?
という訳で4秒後にCAしました...
F, G
分かりません!w
卬高杯2はtori9さんの問題が多いので心配です...
結果
![]()
3ペナ5完で、15位でした!ひゃっほう!
参加人数が少ないというのもありましたが、嬉しいです!
ついでに先に5完された某せぶんてぃーん君にも勝てたのでうれs... おっと誰か来たようですね、お届け物でしょうk
さて次回はOMC050です!
友達がFのwriterをやっているので、解きたいです!
