フーリエ級数を用いて画像をピカソ画に

はじめに

フーリエ級数についての動画を見ていたら、動画内で絵をフーリエで表している場面があり気に入ったので実際にやってみることにしました。タイトルのピカソ画にはピカソにも似たような作品があったのでそうつけました。

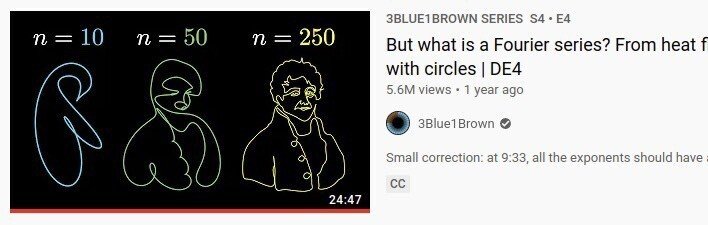
↑　ピカソの一筆書きはこんなやつです。

環境
・Python 3.8
・Ubuntu 20.04
・Jupyter Lab 

ざっくりとした流れ

1. 画像の取得
2. 画像のエッジを取得
3. 取得したエッジを座標入力
4. 入力した座標を一筆書きで線で結ぶ
5. 取得した線をフーリエ変換

1. 画像の取得

今回は画像のエッジを取得するので、エッジがわかりやすく出やすそうで、かつペンギンの以下の画像を選びました。ペンギンかわいい。

2. 画像のエッジを取得

画像のエッジを取得する前に画像の画質を下げます。後々ふれますが、高画質でやると入力した座標を一筆書きで線で結ぶ作業で泣きます。

from PIL import Image

img = Image.open('penguin2.jpeg') #import the image
print(img.size) #check the image size

================
Output:(202, 250)
================

img_resize = img.resize((101, 125))
img_resize = img_resize.save('re_pen2.jpg') #save the resize picture as re_pen2.jpg
print(img_resize.size)

================
Output:(101, 125)
================

画像のサイズは202×250だったので、半分の101×125としました。このくらいのサイズがちょうどいいです、これ以下だと逆に形が変になるし、これ以上だと4でする処理に時間がめっちゃかかります。

リサイズした画像を用いてエッジを取得します

import cv2

# 定数定義
ORG_WINDOW_NAME = "org"
GRAY_WINDOW_NAME = "pen2_gray"
CANNY_WINDOW_NAME = "pen2_canny"

ORG_FILE_NAME = "re_pen2.jpg"
GRAY_FILE_NAME = "pen2_gray.png"
CANNY_FILE_NAME = "pen2_canny.png"

# 元の画像を読み込む
org_img = cv2.imread(ORG_FILE_NAME, cv2.IMREAD_UNCHANGED)
# グレースケールに変換
gray_img = cv2.imread(ORG_FILE_NAME, cv2.IMREAD_GRAYSCALE)
# エッジ抽出
canny_img = cv2.Canny(gray_img, 50, 110)

# ウィンドウに表示
cv2.namedWindow(GRAY_WINDOW_NAME)
cv2.namedWindow(CANNY_WINDOW_NAME)

cv2.imshow(ORG_WINDOW_NAME, org_img)
cv2.imshow(GRAY_WINDOW_NAME, gray_img)
cv2.imshow(CANNY_WINDOW_NAME, canny_img)

# ファイルに保存
cv2.imwrite(GRAY_FILE_NAME, gray_img)
cv2.imwrite(CANNY_FILE_NAME, canny_img)

# 終了処理
cv2.waitKey(0)
cv2.destroyAllWindows()

上の画像を取得できました。うまくエッジが検出できたと思います。

3. 取得したエッジを座標入力

%matplotlib inline
import matplotlib
from matplotlib import pyplot as plt
import numpy as np

img = np.array(Image.open('pen2_canny.png')) #image to array
print(img)
print(img.shape)
================
Output:
[[0 0 0 ... 0 0 0]
[0 0 0 ... 0 0 0]
[0 0 0 ... 0 0 0]
...
[0 0 0 ... 0 0 0]
[0 0 0 ... 0 0 0]
[0 0 0 ... 0 0 0]]
(125, 101)
================

x = np.where(img!=0)[0] 
y = np.where(img!=0)[1]
plt.scatter(x,y,s=1)
plt.grid()
plt.show()

x, y はimgの0ではないところを取得すれば良いので!=0で取得。もちろん白黒なのでimg==255でもok。出力は以下のようになります。ペンギンちゃんが倒れちゃったけど気にせずやりました。ちなみに点は699個ありました。

4. 入力した座標を一筆書きで線で結ぶ

3でプロットしたのでそれを線でうまく一筆書きします。これが思った以上に大変でした。どうやら、巡回セールスマン問題っていうNP-hardな有名な問題でした。(リンクはwikipedia)　

巡回セールスマン問題は普通に解くとスパコンでもえげつない時間がかかるので近似解を求めます。2で画像サイズを下げたのは近似解でも単純に処理に時間かかるからです。色々な近似解法があるらしいですが、今回は2-opt法を用います。詳しくは最後に参考元にしたURLを貼ったのでそちらを見てください。

ランダムに線をつなげる

import numpy.random as nr 

nr.seed(1) 
num = x.shape[0]　#699(number of plot)

#random 
para = np.arange(num)
nr.shuffle(para)
print(para)

#plot
plt.figure(figsize=(6, 6))
plt.plot(x[para], y[para], 'ok-')
plt.xlabel('x'); plt.ylabel('y')
plt.show()

2-optを用いて最適化

from vcopt import vcopt

def tsp_score(para):
   return np.sum(((x[para][:-1] - x[para][1:])**2 + (y[para][:-1] - y[para][1:])**2)**0.5)

#paraの可視化
def tsp_show_para(para, **info):
 #2-opt処理中の諸情報はinfoという辞書に格納されて渡されます
 #これらを受け取って使用することができます
   step_num = info['step_num']
   score = info['score']
   if (step_num%100)==0:
       #プロット（および保存）
       plt.figure()
       plt.plot(x[para], y[para], 'ok-')
       plt.xlabel('x'); plt.ylabel('y')
       plt.title('step={}, score={}'.format(step_num, score))
       plt.savefig('save/{}.png'.format(step_num))
       plt.show()
       print()

可視化は一回ずつplotしていては数が膨大になるので100stepsごとにplotします。

nr.seed(1)
num = x.shape[0] #699

#適当に道順を作成
para = np.arange(num)

#2-opt法で最適化
para, score = vcopt().opt2(para,                          #para
                          tsp_score,                     #score_func
                          0.0,                           #aim
                          show_para_func=tsp_show_para,  #show_para_func=None
                          seed=1)                        #seed=None

#結果の表示
print(para)
print(score)

実行結果です。gifにすると最適化されてるのがわかりやすい。大体2500スッテプくらいでした。最適化されたルートはparaに保存されているので、xpos = x[para], ypos = y[para]と以下のようにする事で座標上で一筆書きのルートが確認できます。

xpos = x[para]
ypos = y[para]
plt.plot(xpos, ypos)
plt.grid()
plt.show()

最終的にこのような一筆書きのルートになりました。どう見てもペンギンです。

5. 取得した線をフーリエ変換

X = np.fft.fft(xpos)
Y = np.fft.fft(ypos)

nlim = 10 #The parameter

N = X.shape[0]
s = np.arange(0,N,1.0)
x_data = X[0] * np.cos(2*np.pi*0.0/N*s)/N
y_data = Y[0] * np.cos(2*np.pi*0.0/N*s)/N
for n in range(1,nlim+1):
   xan = (X[n] - X[N-n]) * (0.0 + 1.0j)
   xbn = (X[n] + X[N-n])
   yan = (Y[n] - Y[N-n]) * (0.0 + 1.0j)
   ybn = (Y[n] + Y[N-n])
   x_data = x_data + xan * np.sin(2*np.pi*n/N*s)/N + xbn * np.cos(2*np.pi*n/N*s)/N
   y_data = y_data + yan * np.sin(2*np.pi*n/N*s)/N + ybn * np.cos(2*np.pi*n/N*s)/N

plt.plot(np.real(x_data), np.real(y_data),label='n = '+str(nlim),color ='black')
plt.legend()
plt.show()

パラメータは n = 10でやってみます。　さあ、どうなる。

…うん、ペンギンです。わからない人は芸術のセンスがないです。僕にはペンギンに見えます。

パラメータを n = 10, 20, 30, 40, 60, 100, 200, 300, 400 と変えて出力してみました。わかりやすいようにペンギンを立たせました。

パラメータを増やすほど4で得たペンギンに近づくのがわかると思います。

反省

思った以上にペンギンに見えなかった。思ったんとちゃうかった。以下の画像のようなものを期待していた。ルートがわるかったと思う、なんか腹つっきってるし。画像処理をちゃんとやるか、一筆書きのルートを工夫すれば、もうちょい綺麗になると思う。あと、巡回セールスマン問題(TSP)の近似解法ももうちょい処理が早い方法があると思う。

感想

フーリエ変換でっていうより、巡回セールスマン問題でした。思った以上に大変だったけど、グラフ理論などもちょっとだけ学べたので良かったです。何より自分で出力した画像は愛着がわきます。正直いうとペンギンか？って思ったけどこれも芸術です。

参考URL

・情報基礎 「Pythonプログラミング」（ステップ７・リスト・フーリエ級数）
・But what is a Fourier series? From heat flow to drawing with circles | DE4
・巡回セールスマン問題を2-opt法で解く（Python）