
多重共線性ってなんやねんを確認する
こんにちは、今回は多重共線性について書いていきます。本やブログでは「予測モデルを作成するときに、説明変数に多重共線性(or マルチコ)があるかを確認し、もしある場合は無くなるように調整しましょう。」という趣旨でよく説明されています。
しかし、多重共線性があるときにどのようなことが起こって、モデルに影響があるかを説明しているものは多くない印象でした。
そこで、R言語でシミュレーションして多重回帰モデル上での多重共線性発生時の振る舞いを確認してみました。
コード類は↓です。(短時間で作った雑コードなので詳しい解説は省きます。)
多重共線性とは
多重共線性とは、モデルに使用する説明変数間に強い相関がある状況を指します。
多重共線性がある状態での重回帰モデルについて、回帰係数のバラツキが大きくなることが明らかになっています。これは、説明変数が目的変数にどれだけ効果があるか(条件付平均値)を推定したい重回帰モデルにおいて致命傷です。
これを大雑把に言うと、回帰係数の導出過程において出てくる分散共分散行列の行列式が小さくなりやすくなり、データの性質以上に係数を多く見積もってしまうからです。
さらに言うと、完全に同じである2つのデータを説明変数とした場合は分散共分散行列の行列式が0となり、逆行列が求まらない(低ランクといいます)=回帰係数を求めることができません。
シミュレーションによる検証
多重共線性があると回帰係数に悪影響があると言われてもどれだけ気を付けるべきなのかはよく分かりませんでした。そこで、疑似データを使ったシミュレーションで、多重共線性の強さを回帰係数の関係性を確認してみます。
疑似データの作成
今回は2変数を説明変数とした以下の重回帰モデルを使用します。(回帰係数も固定して定数とみなします)
$$
y = \alpha_{1} x_{1} + \alpha_{2} x_{2} + \epsilon
$$
データ生成のフローは次の通りにしました。これにより、多重共線性の強さ=相関係数およびサンプルサイズを変えた場合の回帰係数の安定性を評価することができます。
サンプルサイズを決める
定めた相関係数に近い説明変数$${x_{1}, x_{2}}$$の組を生成する
↑の重回帰モデルに当てはめた$${y}$$を生成する
$${y \sim x_{1} + x_{2}}$$で重回帰分析を行い、回帰係数を導出する
2 ~ 4を100回繰り返し、得られた回帰係数群の標準偏差を計算する
実際に生成した$${x_{1}, x_{2}}$$の組は以下のようになります。



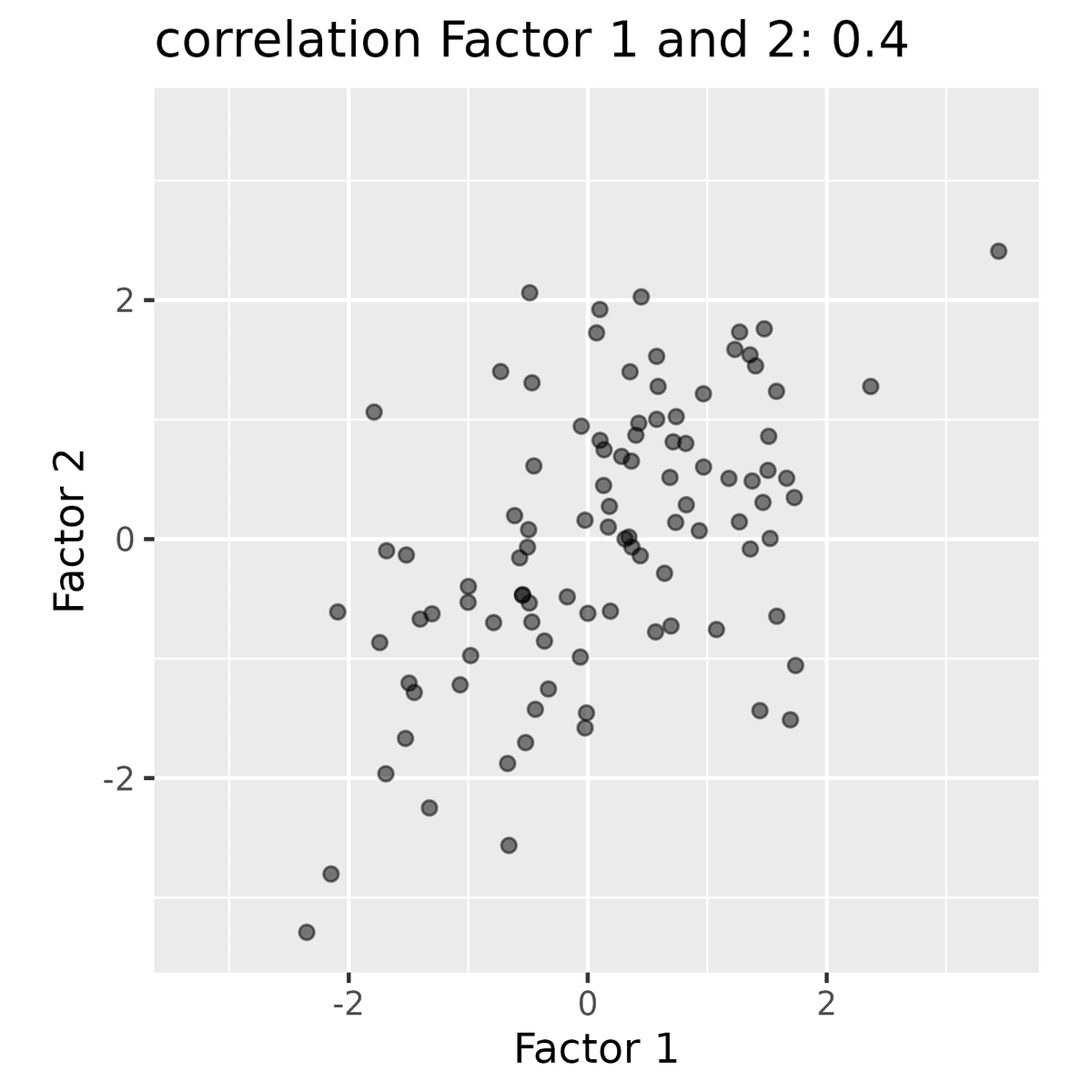

人によっては共通テストを思い浮かべるかもしれませんがw、おおよそよいデータが生成できました。
回帰係数の安定性評価
ということで、シミュレーションによる結果は以下のグラフのようになりました。縦軸が標準偏差、横軸がシミュレーション時の相関係数、色はサンプルサイズによって分けています。

これらから、以下のことが言えます。
相関が強いほど回帰係数の標準偏差が大きい
特に、強相関と無相関を比較すると倍くらい差がある
サンプルサイズが大きいほど回帰係数の標準偏差が小さい
$$\mathcal{O}(n^{10})$$では、相関係数よりも影響が大きい
確かに、最初に確認したかった「多重共線性がある状態での重回帰モデルについて、回帰係数のバラツキが大きくなる」現象が再現できました。相関が強くなるだけで標準偏差が大きくなってしまうので、確かにこれは要注意です。
他モデルでの多重共線性
シミュレーション上では多重回帰モデルでの振る舞いを確認しましたが、他モデルでも多重共線性は予測精度や汎化性能に影響を及ぼすことが分かっています。
例えば、回帰とは全く導出過程が異なる決定木系モデルでも重要特徴量の振る舞いが安定しないといったことが明らかになっています。(詳しくは次のきじを参照ください)
ということで、多重共線性について簡単に検証してみました。理論を実験で検証することはかなり大事ですし、実際にどれ程変わるかを確認できるので実データの分析においてもセンスが磨かれていきます。
皆様も気になったことは実験してみて、納得感を得て、理解度も深めていっちゃいましょう。
と、ここまで書いてもっと複雑な実験がしたくなったのでまた記事に書いていきます!
最後までお読みいただきありがとうございました。
いいなと思ったら応援しよう!

