
MATLAB/Simulink でアルゴリズム開発 ~ C/C++ の検証を MATLAB で ~ C Caller / C Function
まえがき
私は通常、MATLAB/Simulink でアルゴリズム開発を行い、組み込み・VST(JUCE)用に C/C++ 化を行うことが多いです。
その場合、検証用テストデータの作成および、C/C++ での実行結果の検証にも MATLAB/Simulink を使います。
これだけでもかなり効率的ではあるのですが、テストデータを C/C++ に持って行ったり、実行結果を MATLAB に持っていったりと、MATLAB <-> C/C++ 開発環境の行ったり来たりが面倒です。
できれば、なるべく行ったり来たりせずに MATLAB 上で行いたいところ。
Simulink で C/C++
実は Simulink には、C/C++ のソースコードを取り込んで実行する機能があります。
主なブロックは3つ
・C Caller (R2018b~)
単純な C コード呼出しの場合
・C Function(R2020a~)
メモリの割り当て・解除、前処理・後処理、永続データを使う場合
・S-Function
動的システムを統合する場合
比較的最近、新たな機能ブロックが追加されています。
今回はこの新たに実装された、簡単に使える C Caller / C Function について解説しようと思います。
前準備
・使用コンパイラの設定
>> mex -setup cpp
で、使用するコンパイラを指定しておいてください。
・In-Process and Out-of-Process Simulation 設定
モデルコンフィグレーションパラメータ(Ctrl-E)-> シミュレーションターゲット -> インポート設定 で
「カスタムコードのシミュレーションを別のプロセスで行う」
をチェックしておくとコンパイルから外部プロセスで行われ、C/C++ コード内のエラーで MATLAB が落ちることがないので便利です。私の場合、In-Process で発生していたエラーメッセージの文字化けもこれで解決しました。

C Caller
一番簡単なのは C Caller で、基本的には C のソースコードをそのまま取り込めば良いだけです。
クロスオーバーフィルター(Linkwitz-Riley フィルター)
例として、オーディオのクロスオーバーフィルターとしてよく使われる、Linkwitz-Riley フィルターを作ってみましょう。
通過帯域の周波数特性が最大限平坦で位相特性にも優れるバタワースフィルターを2段重ねにすることでクロスオーバー周波数でのゲインを -6dB とし、合成信号が元に戻るよう設計されたフィルターです。
Audio Toolbox には、crossoverFilter 関数が用意されています。
crossFilt = crossoverFilter('CrossoverFrequencies',1000, 'SampleRate', 48000);
visualize(crossFilt)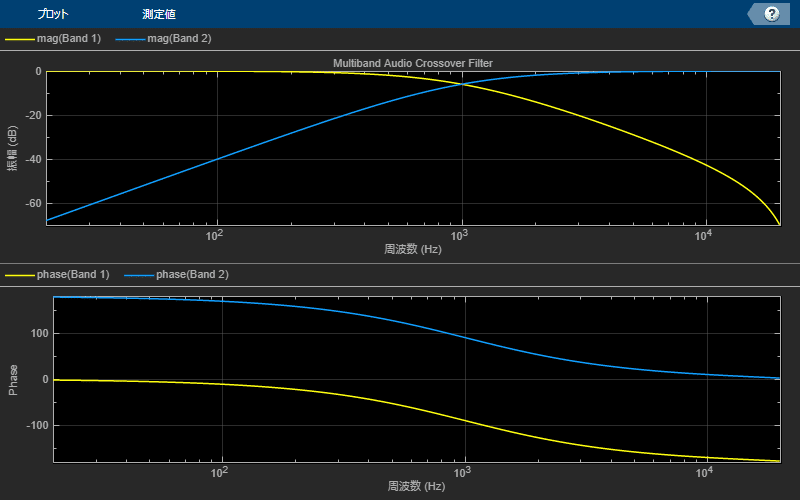
2段重ねなのでフィルター係数用変数も2次元配列としたいところですが、C Caller ではダブルポインターが使えないようなので、バタワースフィルター係数(1次元配列)だけ作って、周波数特性表示の時に2段重ねにします。(なので、作ってるのはバタワースですが・・)
まずは、calcLRcross_c.h、calcLRcross_c.c 2つのファイルを作ります。
#ifndef _CALCLRCROSS_C_H_
#define _CALCLRCROSS_C_H_
extern void calculateCoefficientsButterworth(double Fc, double *sosPEQ_L, double *sosPEQ_H);
#endifcalcLRcross_c.h
#include "calcLRcross_c.h"
#define _USE_MATH_DEFINES
#include <math.h>
void calculateCoefficientsButterworth(double Fc, double *sosPEQ_L, double *sosPEQ_H)
{
double W, N, B0, B1, B2, A1, A2;
double Fs = 48000.0;
W = tan(M_PI*Fc/Fs);
// LPF
N = 1/(1+W);
B0 = W*N;
B1 = B0;
A1 = N*(W-1);
sosPEQ_L[0] = B0; sosPEQ_L[1] = B1; sosPEQ_L[2] = 0.0f;
sosPEQ_L[3] = 1.0f; sosPEQ_L[4] = A1; sosPEQ_L[5] = 0.0f;
// HPF
N = 1/(1+W);
B0 = N;
B1 = -B0;
A1 = N*(W-1);
sosPEQ_H[0] = B0; sosPEQ_H[1] = B1; sosPEQ_H[2] = 0.0f;
sosPEQ_H[3] = 1.0f; sosPEQ_H[4] = A1; sosPEQ_H[5] = 0.0f;
}calcLRcross_c.c
後ほど説明する biquad フィルター係数 B2、A2 相当が 0 なのでそこは必要ないのですが、MATLAB のフィルターオブジェクトの係数基本単位が 2x6 なので、MATLAB でも取り扱いやすいよう確保しておきます。
次にこれを、Simulink に読み込みます。
新規 Simulink モデル作成
モデルコンフィグレーションパラメータ(Ctrl-E)-> シミュレーションターゲット
コード情報
インクルードヘッダー:#include "calcCoeff_c.h"
ソースファイル:calcCoeff_c.cOK
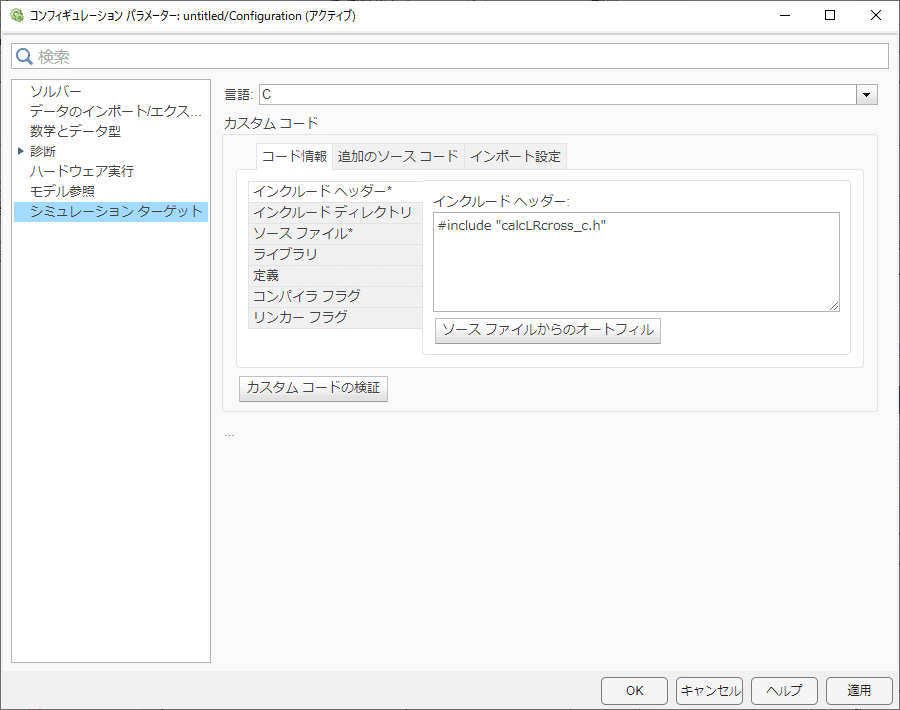
続いて C Caller ブロックを置き、ダブルクリックで開き、「カスタムコードを更新」します。

問題がなければ診断ビューアに「正常に完了しました」のメッセージが出ますので、OKでブロックパラメータを閉じます。
すると <FunctionName> に関数一覧が登録されているはずです。
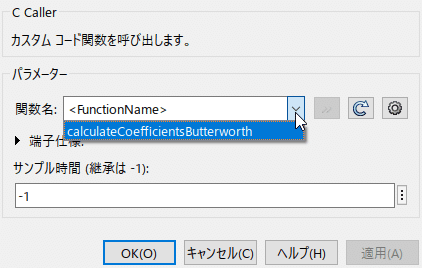
C のソースコードにエラーがあると登録されないので、事前に普通のデバッグは C の開発環境で済ませておいた方が良いでしょう。今回のは簡単な例なので、一度も C の IDE は開かずにやりましたが。
ここで「関数名」に呼び出したい関数を選択すると、自動的に「端子仕様」に引数一覧が登録されます。
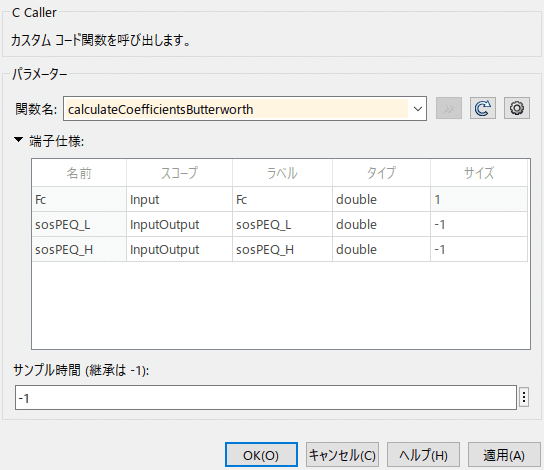
そのまま OK すれば、ブロックが更新されて入出力端子が登録されます。

あとは普通にモデルを作成するだけです。ここでは、MATLAB の crossoverFilter 関数との比較も入れてみました。(要 Audio Toolbox)

function [y_L, y_H] = fcn(Fc)
persistent crossFilt
cN = 1;
if isempty(crossFilt)
crossFilt = crossoverFilter('NumCrossovers',cN, ...
'CrossoverFrequencies',Fc, 'SampleRate', 48000);
else
crossFilt.CrossoverFrequencies = Fc;
end
[B_L, A_L, B_H, A_H] = getFilterCoefficients(crossFilt,cN);
y_L = [B_L A_L];
y_H = [B_H A_H];MATLAB crossoverFilter(MATLAB Function ブロック)
function fcn(coeff1_L, coeff1_H, coeff2_L, coeff2_H)
persistent ax1 ax2 ax3 ax4
fs = 48000;
if isempty(ax1)
figure(1)
sosPEQ = [coeff1_L; coeff1_L];
[h,f] = freqz(sosPEQ,8192,fs);
hdB = 20*log10(abs(h));
ax1 = semilogx(f, hdB, DisplayName='LPF1');
hold on
ax2 = semilogx(f, hdB, DisplayName='HPF1');
ax3 = semilogx(f, hdB, '--', DisplayName='LPF2',LineWidth=1.5);
ax4 = semilogx(f, hdB, '--', DisplayName='HPF2',LineWidth=1.5);
hold off
end
sosPEQ = [coeff1_L; coeff1_L];
[h,~] = freqz(sosPEQ,8192,fs);
hdB = 20*log10(abs(h));
set(ax1,'YData',hdB)
xlim([20 fs/2])
grid on
sosPEQ = [coeff1_H; coeff1_H];
[h,~] = freqz(sosPEQ,8192,fs);
hdB = 20*log10(abs(h));
set(ax2,'YData',hdB)
sosPEQ = coeff2_L;
[h,~] = freqz(sosPEQ,8192,fs);
hdB = 20*log10(abs(h));
set(ax3,'YData',hdB)
sosPEQ = coeff2_H;
[h,~] = freqz(sosPEQ,8192,fs);
hdB = 20*log10(abs(h));
set(ax4,'YData',hdB)
ylim([-80 0])
legend(Location="best")
drawnowPlot Frequency Response(MATLAB Function ブロック)
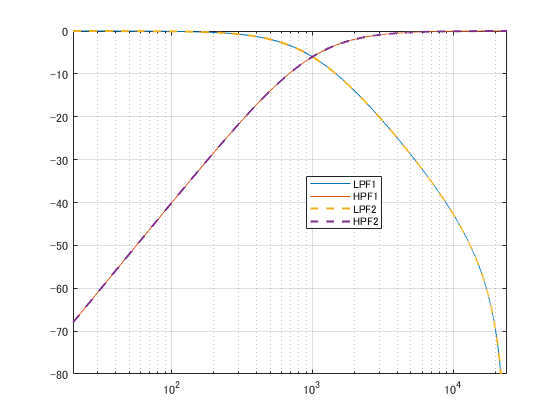
MATLAB 関数の結果とも一致しているようです。
モデル例(R2022b)
C Function
C Caller は一番簡単に使えるのですが、メモリの割り当てもできず、ダブルポインターも使えず、C++ も非対応であるため、より適用範囲が広く C++ も対応の C Function の方が使い勝手は良いと思います。
ダブルポインターは、C Function でも使えないようです・・
Bi-quad(双2次)フィルターの周波数特性を求める
まずは、題材とする biquad フィルターの周波数特性を求める式を C++ で書きます。
biquad フィルターの構造は例えば以下のブロック図で表され、各係数(B0-2、A1-2)を書き換えることで、ローパス/ハイパス、ローシェルフ/ハイシェルフ、ピーク/ノッチ、バンドパス/エリミネート、オールパス等、各種フィルターを実現することができます。
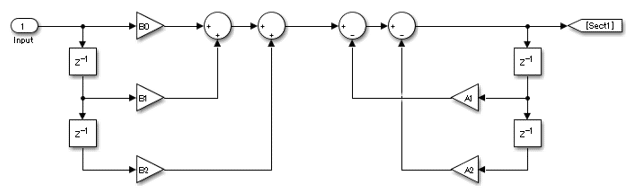
設計例はこちらの記事に載せてあります。
フィードバック側係数のデフォルト符号がまちまちであることがあるので気をつけてください。MATLABは上の構成例に示したように "-" です。
biquad フィルターの伝達関数を z 変換で表すと、構成図から
$$
H(z)=\frac{B_0+B_1z^{-1}+B_2z^{-2}}{1+A_1z^{-1}+A_2z^{-2}}
$$
となります。
z 変換の定義式
$$
X(z)=\sum x_nz^{-n}
$$
と
フーリエ変換の定義式
$$
X(\omega)=\sum x_ne^{-j\omega n}
$$
を比べると、z 変換の式で $${z=e^{j\omega}}$$ と置換すれば、フーリエ変換となり、周波数特性が求まることが分かります。
まずは MATLAB で確認してみます。
fs = 48000;
crossFilt = crossoverFilter('CrossoverFrequencies',1000, 'SampleRate', fs);
[B, A] = getFilterCoefficients(crossFilt,1);
st = pi/512;
w = (0:st:pi-st)';
sosPEQ =[B(1,:) A(1,:)];
h = zeros(size(w));
for k = 1:length(w)
h(k) = (sosPEQ(1,1) + sosPEQ(1,2) * exp(-1i*w(k)) + sosPEQ(1,3) * exp(-1i*2*w(k))) ...
/ (1 + sosPEQ(1,5) * exp(-1i*w(k)) + sosPEQ(1,6) * exp(-1i*2*w(k)));
end
hdB = 20*log10(abs(h));
semilogx(w/(2*pi)*fs,hdB)
hold on
sosPEQ = [sosPEQ; 1 0 0 1 0 0];
[h, w] = freqz(sosPEQ,512);
hdB = 20*log10(abs(h));
semilogx(f,hdB,'--')
hold off
gid on
xlim([20 fs/2])
max(abs(hdB-hdB2))freqz() の結果とも、最大誤差 4.5e-13 dB で一致します。
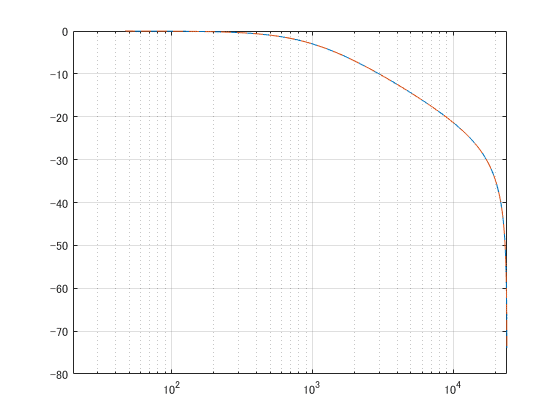
これを C++ で書くと以下のようになります。
#ifndef _CALCFRES_CPP_
#define _CALCFRES_CPP_
class peq {
public:
peq(); // constructor
void calcFres(float * coeff, float * hmag);
};
#endif /* _CALCFRES__ */calcFres_cpp.h
#include "calcFres_cpp.h"
#include <stdlib.h>
#define _USE_MATH_DEFINES
#include <math.h>
#include <complex>
using namespace std;
peq::peq()
{
}
void peq::calcFres(float* coeff, float* hmag)
{
float st = M_PI / 512.0f;
float w = 0.0f;
int32_t k = 0;
complex<float> h;
complex<float> mI(0.0f,-1.0f);
for (k = 0; k < 512; k++) {
w = st * k;
h = (coeff[0] + coeff[1] * exp(mI * w) + coeff[2] * exp(mI * 2.0f * w))
/ (1.0f + coeff[4] * exp(mI * w) + coeff[5] * exp(mI * 2.0f * w));
hmag[k] = abs(h);
}
}calcFres_cpp.cpp
C Functionでは、以下のように設定します。
新規 Simulink モデル作成
モデルコンフィグレーションパラメータ(Ctrl-E)-> シミュレーションターゲット
コード情報
言語:C++
インクルードヘッダー:#include "calcFres_cpp.h"
ソースファイル:calcFres_cpp.cppOK
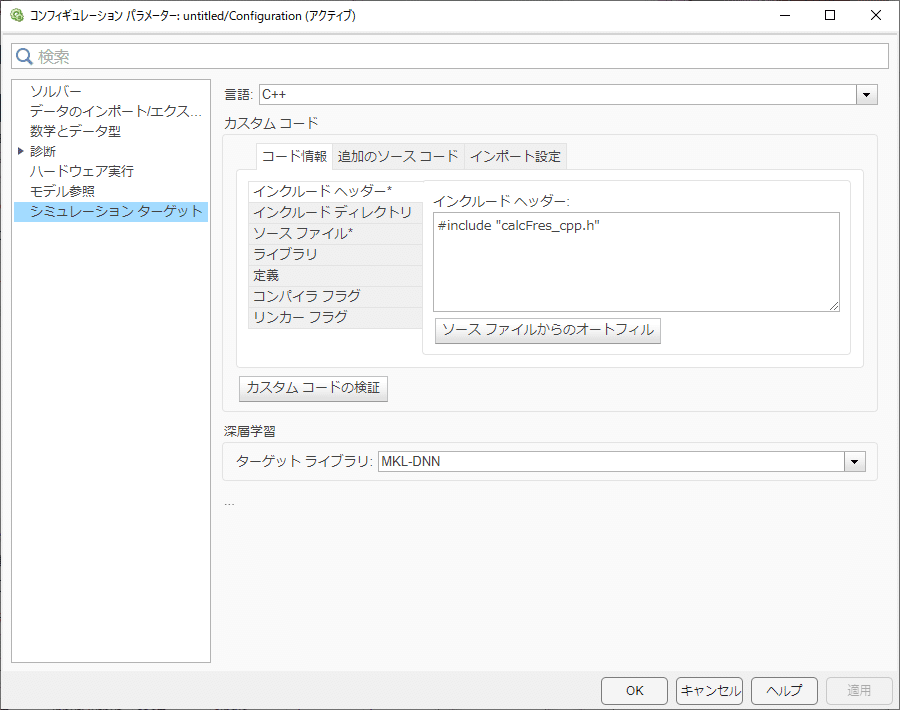
次に C Caller の時と同様に、C Function ブロックを置き、ダブルクリックで開き、以下のように設定します。
C Caller の様に自動で出てこないようなので、自分で入力する必要があります。
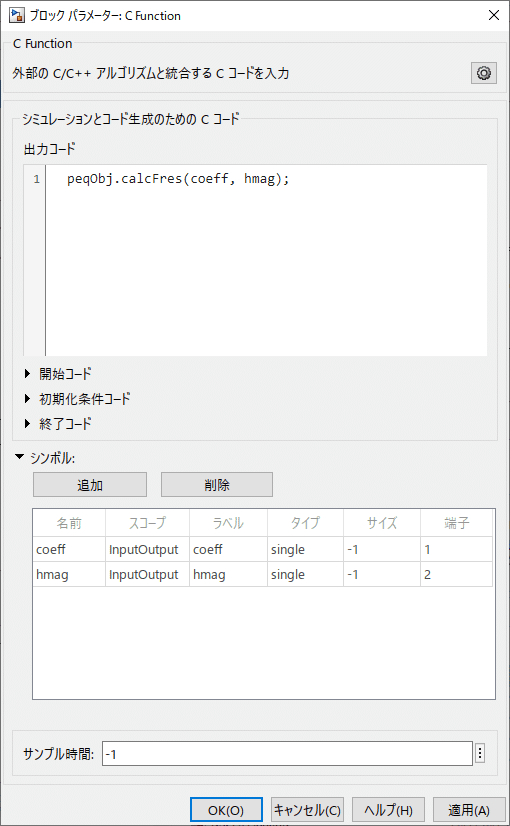
出力コード -> peqObj.calcFres(coeff, hmag);
シンボル:
追加して、名前をそれぞれ coeff、hmagに変え、スコープを InputOutput、タイプを single、サイズを -1(継承)に設定します。
main 関数相当(オブジェクト生成)は、ブロックパラメータのシンボルで定義します。
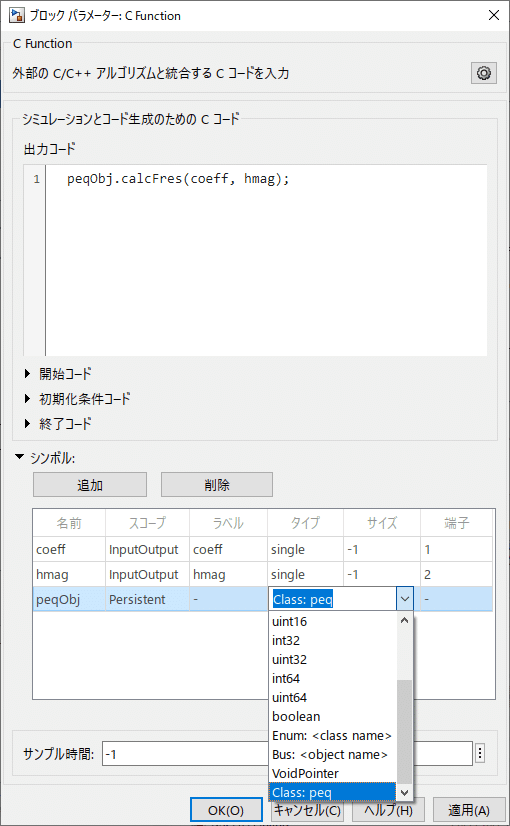
シンボルの追加で peqObj、Persistentと設定すると、タイプの一覧にクラスが出てくるのでこれを選択します。
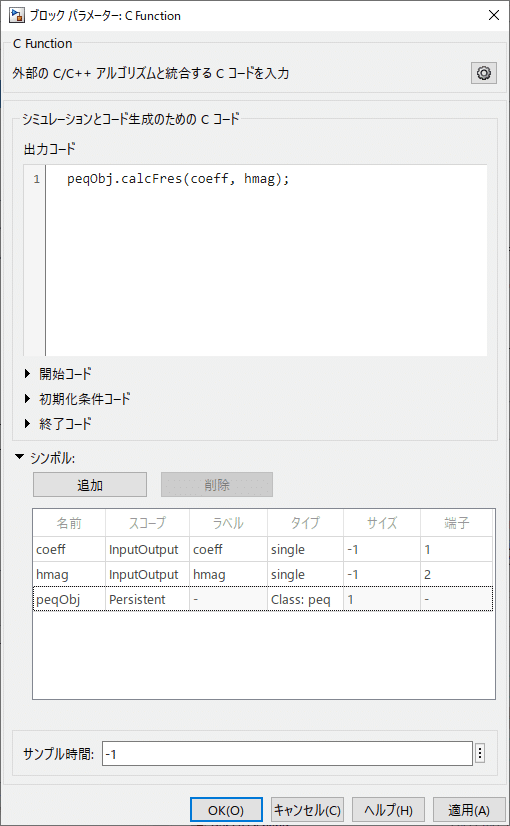
OK で戻ると入出力端子が登録されているはずです。
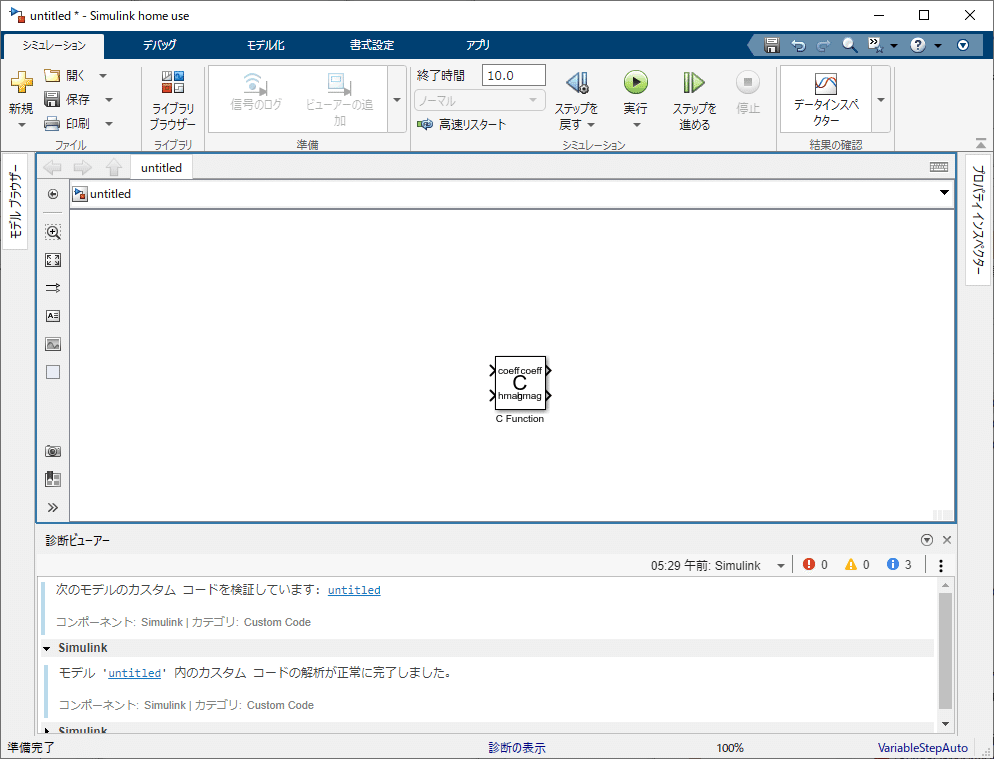
あとはこちらも、普通にモデルを作成するだけです。

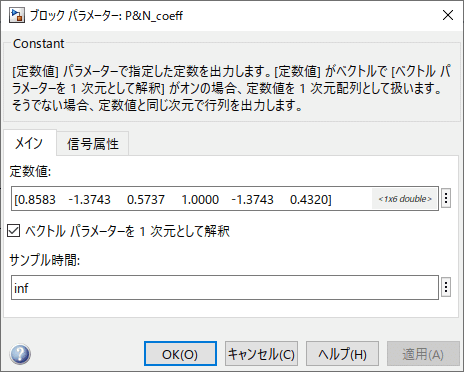
C Caller で使ったクロスオーバーフィルターは 0 係数があるため、別途ノッチフィルター係数 [0.8583 -1.3743 0.5737 1.0000 -1.3743 0.4320] を入れてみました。
function fcn(coeff,hmag)
fs = 44100;
st = pi/512;
w = (0:st:pi-st)';
sosPEQ = [coeff'; 1 0 0 1 0 0];
figure(1)
h_dB = 20 * log10(hmag);
semilogx(h_dB,DisplayName='C++')
grid on
hold on
[hm,~] = freqz(sosPEQ);
hm_dB = 20 * log10(abs(hm));
semilogx(hm_dB,'--',LineWidth=1.5,DisplayName='MATLAB')
hold off
maxErr = max(abs(hm_dB-h_dB));
strtmp = sprintf('max error = %g dB',maxErr);
text(400,-3,strtmp)
legend;
xlabel('Frequency (Hz)')
ylabel('Gain (dB)')
grid on
xlim([w(1)/(2*pi)*fs w(end)/(2*pi)*fs]);Plot2(MATLAB Function ブロック)
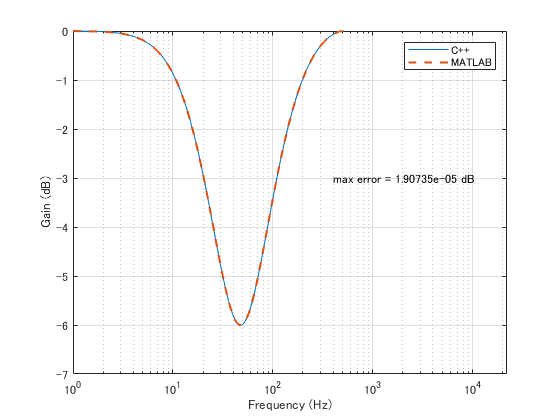
良さそうですね。
モデル例(R2022b)
あとがき
以前は、インターフェースの設定が色々と面倒な S-Function しかなかったのですが、R2018b で C Caller が、R2020a で C Function が追加され、より簡単に C/C++ を取り込むことができるようになりました。
これで、MATLAB/Simulink でアルゴリズム開発を行い、組み込み・VST(JUCE)用に C/C++ 化を行う場合のネックであった MATLAB <-> C のIDE の行き来がかなり緩和されそうです。(-_☆)
全てが MATLAB で完結して欲しい。( ̄ー ̄;
