
音量やデータを滑らかに変化させる ~ 積分器で簡単に
まえがき
VST 等、オーディオの内部処理で音量を変えたりする場合、急に大きく変えると波形が不連続となり、「プチッ」というノイズが出ることがあります。
そのため、音量を滑らかに変化させる必要があります。
(振幅が小さいところで切り替わると気にならず、テストでは気付かないことがあるので注意が必要です)
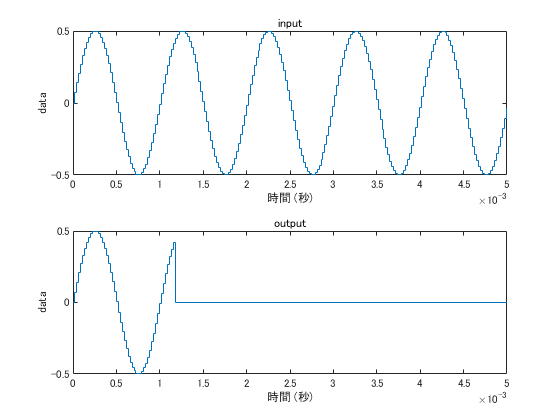
ランプ関数
JUCE のチュートリアルでは、前の Gain と比べて違ってたら、その間を applyGainRamp() によってフレーム内で滑らかに変化させる例が載っています。
if (juce::approximatelyEqual (currentGain, previousGain))
{
buffer.applyGain (currentGain);
}
else
{
buffer.applyGainRamp (0, buffer.getNumSamples(), previousGain, currentGain);
previousGain = currentGain;
}applyGainRamp() は、previousGain ~ currentGain 間を getNumSamples かけてリニアにゲインを適用します。
REAPER の JSFX スケルトンのゲイン調整も同様に、変化分をフレームサイズで割って += しています。
d_gain = (next_gain - last_gain)/samplesblock;
last_gain += d_gain;ただこれらの方法では、変化時間(時定数)がフレームサイズに依存します。
フレームサイズはユーザーによって変更可能な数値です。
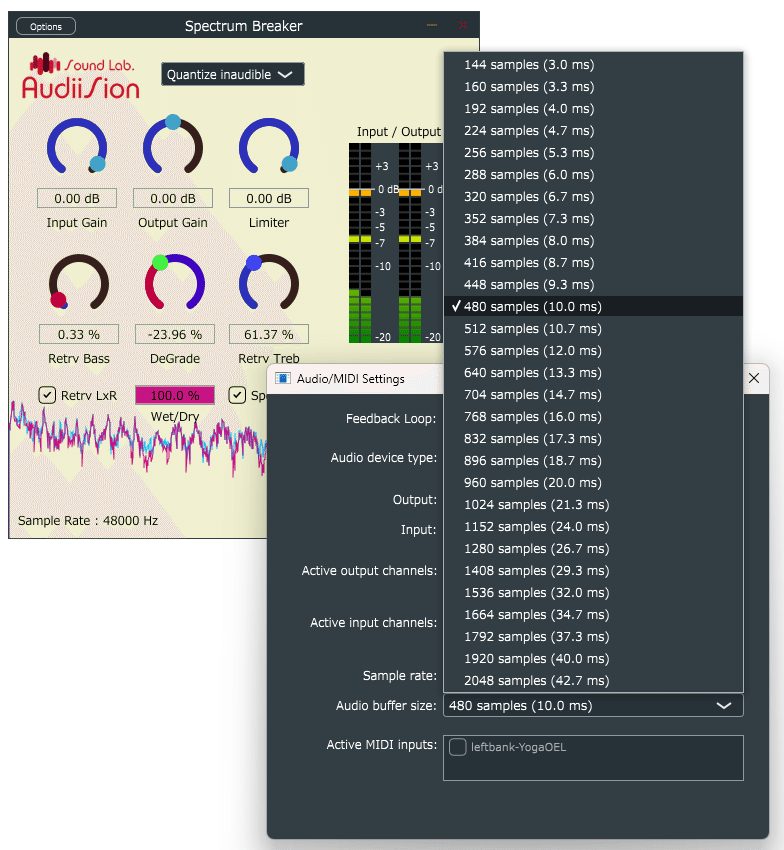
そのため想定外の動作となる場合もあり、フレームサイズに寄らず時定数を一定にしたい場合などは、多少面倒な処理が必要になってしまいます。
積分器(LPF)を使う
ゲインを滑らかに変化させるには、切替信号を積分器に通す方法があります。
Fade(t) = SW*e + (1-e)*Fade(t-1)
Fade:ゲイン
SW:切り替え信号
e:時定数係数
あらかじめ滑らかな変化信号を作る必要がなく、途中で切替えても(波形としての)不連続点が出ません。
もちろん時定数が小さすぎると効果がないので、その点は注意が必要です。
伝達関数を求めると
$$
H(z)=\frac{e}{1-(1-e)z^{-1}}
$$
となり、
一般的な IIR フィルターとしても実現できることが分かります。
MATLAB の Biquad Filter を使う場合の係数は
[e 0 0 1 -(1-e) 0]
となります。

(ランプ関数フレーム長 = 1024 サンプル、e = 0.005、Fs = 44.1 kHz)

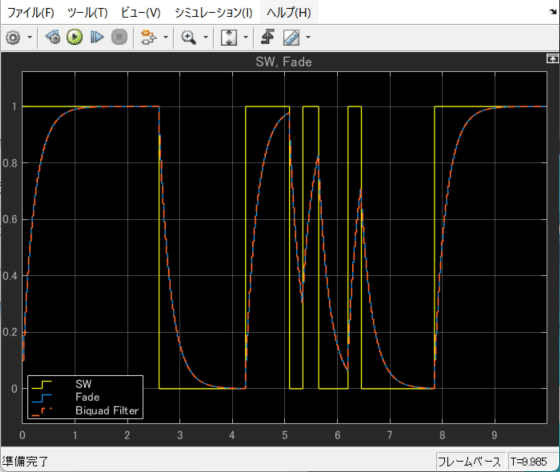
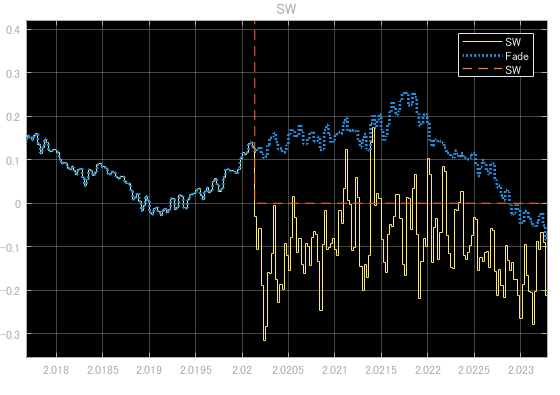
(異なる2曲間の切替え例)
周波数特性としては LPF となります。
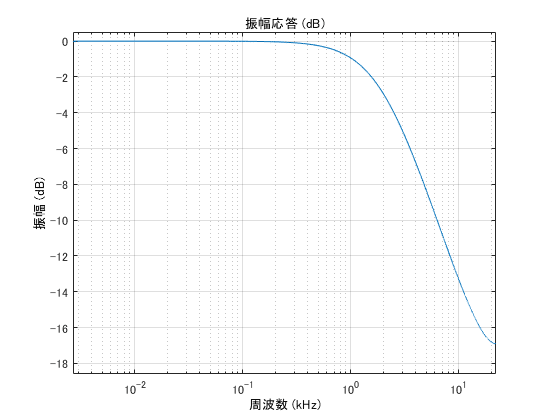
(e = 0.25、Fs = 44.1 kHz)
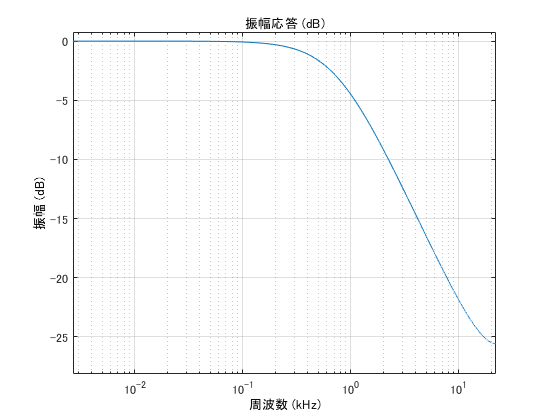
(e = 0.1、Fs = 44.1 kHz)

(e = 0.005、Fs = 44.1 kHz)
・フィルター係数を滑らか変化
またこの方法は、フィルター特性を切り替えるときなどにも使えます。
急にフィルター特性等を切り替えると、やはり音量の急激な変化が起こり、ノイズが発生することがあります。
方法としては、各フィルター係数に同じ積分器を入れるだけです。
MATLAB の公式ドキュメントにも例が載っています。
・移動平均フィルター
一定幅の窓を使って移動させ、その間の平均を求めるのが移動平均フィルターです。
株価変化のグラフなどにも用いられています。
一般的には同じ重みで計算されますが、過去データの影響を時間とともに減少させていく場合にも使えます。
その減少率を一定とすれば、上の例と同じになります。
その場合、時定数係数 e は忘却係数とも呼ばれます。
現在のデータと一つ前の平均だけあれば計算できるので便利です。
過去データ全ての平均を求める場合も、現在のデータと一つ前の平均だけあれば計算はできますが、現在のデータだけ入れれば良いのでより簡単です。
あとがき
ランプ関数よりさらにインプリが簡単で応用範囲も広いので、覚えておくと便利かと思います。
タイトル画像モデル:けいか
