
それってホントに Deep Learning が必要ですか? ~ MATLAB でファジィ推論イコライザー ~ 少ない主観ルールを元に高速推論
まえがき
最近は、なんでも Deep Learning ですね。
すさまじい成果を上げているのでもっともですが、大量の学習データが必要であり、推論時の処理が重いという短所もあります。
ということで今回は世相に反し、少ないルールで構築でき、推論処理も極めて軽いという特徴のある、ファジィ推論を取り上げてみましょう。
自分がファジィ推論をやったことがあるのは大昔で、最近のファジィ界隈がどうなのかよく知らないのですが、MATLAB の Toolbox 製品にもあるくらいなので、基本技術として定着しているのではないかとは思います。
リリースノート見ると、最近も継続的にアップデートされています。
「なんでもファジィ」という時代もありました。
今回は、Fuzzy Logic Toolbox は使っていません。
歴史
ファジィ理論は、1965年にカリフォルニア大バークレイ校の L.A.Zadeh 教授が Information & Control 誌に発表した論文、“Fuzzy Sets(ファジィ集合)” で提唱されました。
"Fuzz" は 「綿毛、毛羽(けば)」 の意味であり、"Fuzzy" とは「輪郭が曖昧な」といった意味を持ちます。
エフェクターの Fuzz は、「毛羽立った」の意味ですかね?
壊れたミキサーにギターを通した音がクールだったのでそのままレコーディングし、その後、「壊れたミキサー」を再現した Fuzz が作られました。
音の輪郭がぼけ、まさしく Fuzzy だったからかもしれません。
その論文で Zadeh は、人間の主観に基づく曖昧さを数学的に厳密に表現することを目的に、輪郭が曖昧な集合、「ファジィ集合」を提案しました。
この論文は実際にはこの2、3年前に書かれましたが、厳密を期する数学に曖昧さを取り入れる、というまったく新しい考えだったためか他の論文誌ではリジェクトされ、しかたなく Zadeh 本人が編集委員をしている Inf. & Cont. 誌に発表したという曰く付きです。
その後、ファジィ集合を元にした推論・制御法などが発表され盛り上がりを見せ始めますが、ある学会では他の研究者との間で「感情的な」議論に発展するなど根強いファジィ不要論(「通常の PID 制御の特殊な例に過ぎない」等)があったようです。
しかし、主観的なルールを元に軽い処理で推論が行えるという点が、それまでシステム化の難しかった、「熟練工がやるとうまくいくが、自動化するとうまくいかない」場合に応用できるのでは?、と着目され、1974年、ロンドン大学の E.H.Mamdani 教授がスチームエンジンのファジィ制御実験により有効性を証明、1980年、デンマーク工科大と Smidth 社によるセメントキルンでのファジィ制御自動運転が開始されました。
80年代後半に入ってからは、「(良い意味での)曖昧さ」が日本人の気質と相性が良かったのか(?)日本を中心に応用例が相次ぎ、PID 制御では簡単にはなし得なかった成果が次々に発表されました。
日本での初の応用例は1987年、新たに開業した仙台市営地下鉄の走行制御で、熟練運転手のようなスムーズな運転が可能になったと言われています。
これはニュースにも大きく取り上げられたため一般社会からも大きな注目を集め、ファジィ家電なども登場、1990年、新語・流行語大賞(新語部門金賞)も受賞するなど、ファジィ・ブームが興ります。(「ファジィ=あいまい」が広まってしまう結果にも・・)
ちなみに、Zadeh 教授の奥さんは(日本人ではありませんが)横浜生まれです。
以下に、日本での初期のファジィ制御応用例をいくつか挙げておきます。
仙台市営地下鉄走行制御(日立)
浄水場薬品注入制御(東京工業大学・富士電機)
シャワー給湯制御(松下住設機器)
エレベータ群管理制御 (三菱・日立・フジテック)
不特定話者音声認識装置 (リコー)
証券投資システム (東京工業大学・山一証券)
甲状腺ガン画像診断システム (川崎医大)
ゴルフ診断システム (マルマンゴルフ)
ファジィ推論とは?
「曖昧さ」とは?
「曖昧さ」にも色々と種類があります。
不完全性(incomplete):知識が不足していて分からない
多義性(ambiguity):解釈が何通りもあって分からない
不正確性(imprecision):誤りが含まれていて正確でない
偶然性(randomness → 確率論):未来のことなので分からない
ファジィネス(fuzziness →ファジィ理論):定義できない・定義しても意味がない、主観によって異なる
ファジィ理論で扱うのは、最後の主観的な曖昧さを含む場合になります。
なぜファジィなのか?
人間の思考や判断は元々曖昧です。
それを数学的に正確に記述しようと思うと、どんどん複雑でわけのわからないものになりがちです。
多くの場合、完全に記述することは不可能で、それを用いて推論や制御を行うには大変な労力が必要となり、なかなかうまくいきません。
しかし、入力・出力ということだけに着目すると言葉で簡単に説明できることが多く、人がやるとうまくできる、という場合が多くあります。
システムの what を問うのでなく、人間ならいかに行動するか(how)を問題にするのがファジィ理論です。
2値論理との比較
トマトの色で熟し具合を判断する例を見てみましょう。
通常の2値論理(クリスプ集合)による三段論法を用いた推論では、
知識:赤いトマトは熟している
事実:このトマトは赤い
結論:このトマトは熟している
となります。
ところが実際にこの推論を機械で行うには、「赤い」を数値で厳密に定義する必要があります。
一方、ファジィ推論では、曖昧さを多値のメンバーシップ関数で表現します。
知識:赤いトマトは熟している
事実:このトマトは少し赤い
結論:このトマトは少し熟している
この結果、一つの知識で人間の感覚に近い推論結果が得られます。
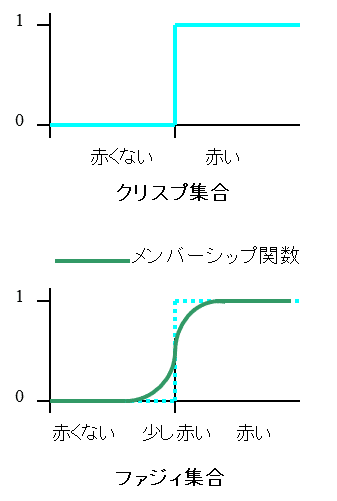
年齢とかも、ある年齢までが「若い」で、それを超えるといきなり「若くない」ということはありませんよね?
ファジィ集合を用いると、そういった境界の曖昧さを保ったまま数学的に扱うことができます。
ウソつきのパラドックス
「私は嘘をつく」
これは2値論理では矛盾しています。
ファジィ推論では「私は嘘をつく」→「私は嘘もつく」として扱えるため、人間の感覚と矛盾しない結果が得られます。
倒立振子制御
制御系の実験でよく見る、棒を台車に付けて立たせるヤツです。

一般的には、ラグランジュ法で運動方程式(微分方程式)を立て、空気抵抗や摩擦抵抗を等価粘性抵抗係数でまとめて表現できると仮定、振子の質量、台車の質量、振子の回転軸から重心までの距離、重心回りの慣性モーメントを代入し、台車の移動方向・速度・加速度の制御を行う・・、とかになるんですかね?
やったことがないので詳しくは知りません。
おそらく、
処理量が多い
滑らかな制御を行おうとするとシステム規模が増大する
各係数をあらかじめ推定しておく必要がある
形状・質量・摩擦係数等、一つでも状態が変ったら破綻する
制御可能範囲が狭い
どこか一カ所でも不具合があれば破綻する
といった課題・問題がありそうです。
しかし、人間は微分方程式などを用いずに、少しの間なら手のひらに乗せた棒を子供でもバランスを取って立たせることができますよね?
それをそのままできるのがファジィ制御です。
ファジィ制御では、例えば以下のような人間が無意識に行っているルール(プロダクション・ルール)を使用して制御を行うことができます。
振子が中くらい傾き、静止している場合:振子の傾きと同じ方向に台車をゆっくり動かす
振子が少し傾き、ゆっくり倒れようとしている場合:振子の傾きと同じ方向に台車を少し速く動かす
振子が少し傾き、ゆっくり戻ろうとしている場合:台車をあまり動かさない
振子がほぼ垂直で、ほぼ静止している場合:台車をあまり動かさない
通常の制御に比べ、以下のような特徴があります。
処理量が少ない
滑らかな制御が可能
各係数をあらかじめ推定しておく必要がない
形状・質量・摩擦係数等、状態が変っても制御できる
制御可能範囲が広い
ルールを丸ごと一つ削除してしまってもそれなりに制御できる
( あくまでも説明用ですので細かいことは突っ込まないでください (^^; )
ファジィ理論
以前作った資料があったので、それを載せておきます。
「ファジィ測度」というのもありますが、ここでは使わないので割愛させていただきます。
ファジィ集合

ファジィ論理

ファジィ推論 (mini-max-重心法)
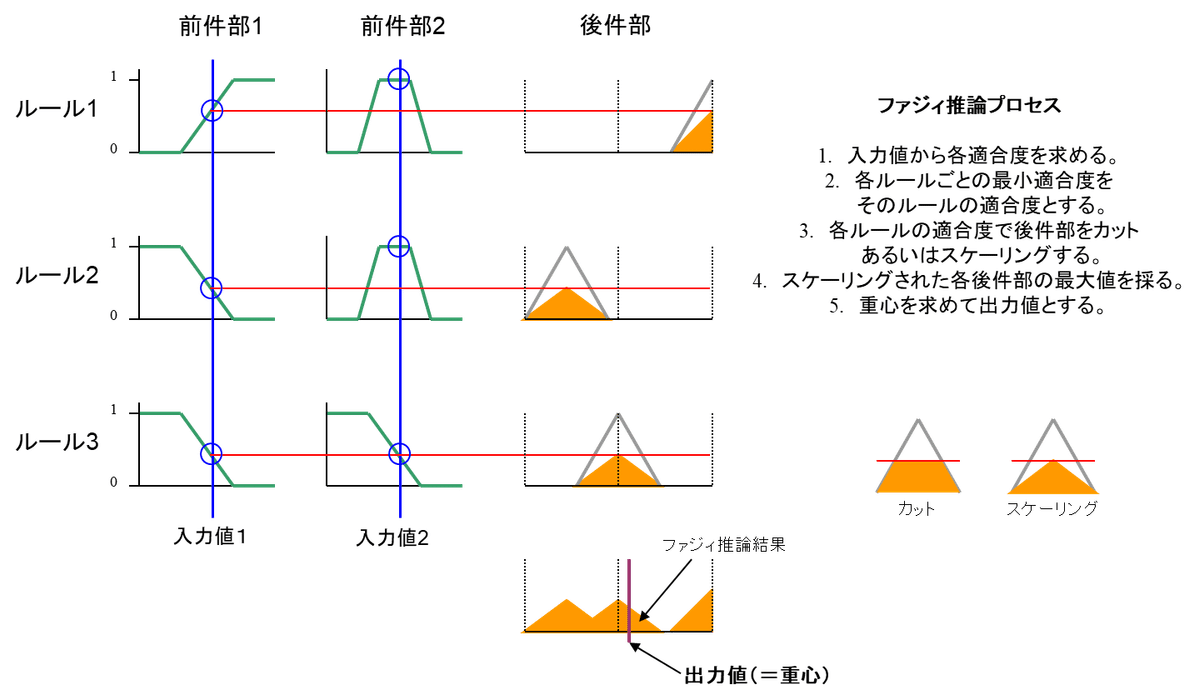
ファジィ推論 (リニア推論法)
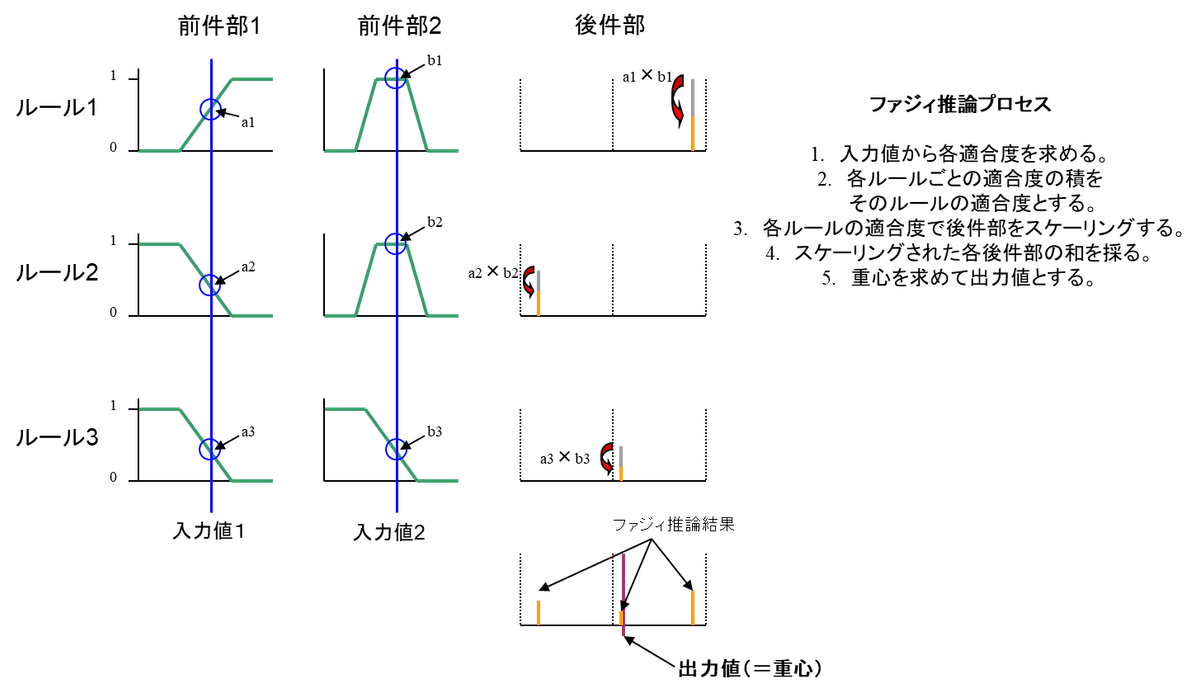
主観的なプロダクション・ルールから、大小比較(mini-max 法の場合)とスケーリングで簡単に推論結果を導くことができます。
ファジィ・イコライザー
ここでは実例として、「綺麗な」「迫力のある」「深みのある」という主観的な特徴量で操作のできるイコライザーを作ってみましょう。
使い方としては、まずは通常のグライコ部で調整を行い、それに対してファジィ・イコライザーで「もう少し穏やかに」「もっと迫力を」といった感覚的な操作を行うことを想定しています。
本当は VST で作りたいところですが、MATLAB の VST はグラフィックが描けず、プログラム中から GUI もいじれないので、AppDesigner を使用します。
私は AppDesigner アプリもまずライブスクリプトで作る事が多いです。
デバッグが楽ですし、アプリへはほぼコピペで済みます。
デバッグも途中結果をライブスクリプトと比べれば良いので、とても効率的に行えます。
因子分析
まずは、感性的な音色表現と周波数特性を結びつける必要があります。
なかなか手頃な研究結果が見当たらなかったのですが、かなり古い独立した研究結果(7),(8) に「3~4つの因子で音色空間の主要部分を表現できる」というのがありました。
それらを元に、3つの因子「美的因子」「迫力因子」「深み因子」を採用し、それぞれの周波数特性を以下のように定義しました。
美的因子:+方向では高低域をカットした穏やかな音色を示し,-方向では高低域をブーストしたいわゆるドンシャリな音色となる
迫力因子:+方向では中域を特に強調して全体域がブーストされ,-方向では逆に中域が最もカットされる
深み因子:+方向では高域がカットされて低域がブーストされ,-方向では逆に低域がカットされて高域がブーストされる
それぞれ最小・最大時(最小= -最大)の周波数特性を以下のように設定し、それと現在のブースト量の差分を出力とします。

もちろんこれらは自由に設定することができ、ファジィ推論アルゴリズム自体は変更不要です。
プロダクション・ルール
前件部として、以下の3つを使用します。
1.中心周波数
2.その周波数の現在のブースト量
3.入力因子操作量(ユーザー操作量)
それぞれに対し同型のメンバーシップ関数、S/M/L を定義します。

後件部は、現在のブースト量に対する差分ブースト量とします。
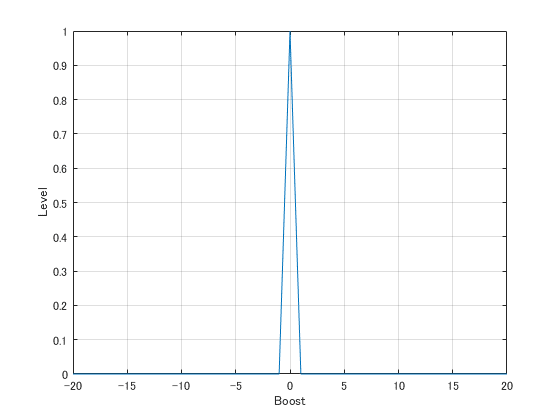
プロダクションルールは各因子ごとに、前件部 S/M/L の全組み合わせ3×3×3= 27 通り(重複順列)が必要になります。
全パターン行列の作り方は、MATLAB でもそのものの関数が見当たらず(どれかでできるような気がするのですが・・)、Web 検索してもかなり複雑なものしか見つからなかったので、少し工夫してみましょう。
例えば0と1の場合、00、01、10、11が生成できれば良いので、2進数の全パターンにあたります。
メンバーシップ関数がn通りだった場合、n進数の前件部数分の桁数の重複順列を作れば良いことになります。
つまり、S = 1; M = 2; L = 3; と置くと、
perm = dec2base(0:26, 3) - '0' + 1;
で簡単に生成できます。
dec2base() の出力は char なので、'0' を引いて数値に変換しています。
perm =
1 1 1
1 1 2
1 1 3
1 2 1
1 2 2
1 2 3
1 3 1
1 3 2
1 3 3
2 1 1
2 1 2
2 1 3
2 2 1
2 2 2
2 2 3
2 3 1
2 3 2
2 3 3
3 1 1
3 1 2
3 1 3
3 2 1
3 2 2
3 2 3
3 3 1
3 3 2
3 3 3@michio_MWJ さんのポストで関数が分かりました!
ID=1:3;
perm = combinations(ID,ID,ID);
でできます。(R2023a 以降)
全プロダクション・ルールを以下に示します。

(出力量もファジィ量を表わす)
例えばルール No.12 は、中域の現在のゲインが小さく、ユーザーが「もっと迫力が欲しい!」とした場合、中域のゲインを大きく上げる、ということを示しています。
各因子に対し前件部は共通で、後件部のみが異なります。
したがって、27×3通りのプロダクション・ルールを持つことになります。
% membership function for S/M/L
S = 1; M = 2; L = 3;
memberShip(:,S) = [ones(1,4) 1:-0.25:0 zeros(1,12)]'; % S
memberShip(:,M) = [zeros(1,4) 0:0.25:1 ones(1,3) 1:-0.25:0 zeros(1,4)]'; % M
memberShip(:,L) = [zeros(1,12) 0:0.25:1 ones(1,4)]'; % L
% production rule
% input:antecedent part, output:consequent part
% ex. now=S and man=S then 7, now=S and man=L then 3
% man S M L S M L S M L
% [7 0 3; 2 0 -2; -3 0 -7]
% now S S S M M M L L L
Beauty_pr(S,:,:) = [7 0 3; 2 0 -2; -3 0 -7]; % for freq is S
Beauty_pr(M,:,:) = [4 0 6; -1 0 1; -6 0 4];
Beauty_pr(L,:,:) = [10 0 0; 5 0 -5; 0 0 -10];
Power_pr(S,:,:) = [2 0 8; -3 0 3; -8 0 -2];
Power_pr(M,:,:) = [0 0 10; -5 0 5; -10 0 0];
Power_pr(L,:,:) = [2 0 8; -3 0 3; -8 0 -2];
Depth_pr(S,:,:) = [2 0 8; -3 0 3; -8 0 -2];
Depth_pr(M,:,:) = [5 0 5; 0 0 0; -5 0 -5];
Depth_pr(L,:,:) = [10 0 0; 5 0 -5; 0 0 -10];
prN = numel(app.Beauty_pr);ファジィ推論部
実際の推論過程は以下のようになります。
各入力に対する適合度(入力値に対する各メンバーシップ関数出力)を求める
ルールごとに、各適合度の最小値で出力メンバーシップ関数をスケーリング
スケーリングされた出力合計の重心を求める
これだけなので、推論自体は数行で行えます。
% fuzzy reasoning
for band = 1:mPEQ.NumEQBands
fIn = mPEQ.Frequencies(band); % each center frequency
fVal = ((log10(fIn) - log10(20)) / (log10(20e3)-log10(20)) * 20) + 1;
nowVal = mPEQ.PeakGains(band) / MaxdB * 10 + 11; % each gain value
F_out = zeros(size(memberShip,1),prN);
minFuzziness = zeros(1,prN);
for p_rule = 1:length(perm)
f = perm(p_rule,1);
now = perm(p_rule,2);
man = perm(p_rule,3);
fuzziness = [interp1(1:21,memberShip(:,f),fVal), ...
interp1(1:21,memberShip(:,now),nowVal), ...
interp1(1:21,memberShip(:,man),manVal)];
minFuzziness(1,p_rule) = min(fuzziness);
out = productionRule(type,f,now,man);
st = 11 - out;
ed = st + 20;
F_out(:,p_rule) = outMmb(st:ed) * min(fuzziness);
end
fuzzy_out = max(F_out,[],2); % take max
crisp_out(1,band) = sum(fuzzy_out .* (1:length(fuzzy_out))') ...
/ sum(fuzzy_out) - 11; % centroid
end
グラフィック・イコライザー
multibandParametricEQ 関数をそのまま使います。
10バンドまでのイコライザーが一つの関数で作れます。
Bands = 7;
CenterFreqs = [60, 150, 400, 1000, 2400, 6000, 15000];
mPEQ = multibandParametricEQ('NumEQBands',Bands, ...
'EQOrder',4, 'SampleRate',fs, ...
'Frequencies',CenterFreqs, ...
'PeakGains',ones(1,7)*0,'QualityFactors',ones(1,7)*1.6);今回はグラフィック上の制限もあり7バンドとしましたが、DFT/DCT を使って人手では調整が難しい数百バンド~としても良いでしょう。
その場合も、基本的にファジィ推論部自体の変更は不要です。
推論過程表示
これが一番大変でした。w
表示スペースの都合もあるので、適合度が0でないルールのみを表示します。
% draw graph of fuzzy reasoning process
f = CenterFreqs(band);
fVal = ((log10(f) - log10(20)) / (log10(20e3)-log10(20)) * 20) + 1;
% draw production rules
r = 1;
for n=find(valuableRule)
% antecedent part
for c=1:3
pobj(r,c).YData = memberShip(:,perm(n,c));
end
% consequent part
pobj(r,4).YData = F_out(:,n);
r = r + 1;
end
% erase non-valuable rules
n=find(valuableRule==0);
for r=1:8-valRuleN
for c=1:3
pobj(valRuleN+r,c).YData = memberShip(:,perm(n(r),c));
end
% consequent part
pobj(valRuleN+r,4).YData = F_out(:,n(r));
end
% draw fitness lines
% must be drawn after each figure
r = 1;
for n=find(valuableRule)
[~,y2] = axesPosition2figurePosition(app,[10,minFuzziness(n)],ax(r,4));
yl = [y2 y2];
p2obj(1,r).Y = yl;
r = r + 1;
end
% erase fitness lines for non-valuable rules
% n=find(valuableRule==0);
for r=1:8-valRuleN
[~,y2] = axesPosition2figurePosition(app,[10,0],ax(valRuleN+r,4));
yl = [y2 y2];
p2obj(1,valRuleN+r).Y = yl;
end
% draw fuzzy output and crisp output
fuzzy_out = max(F_out,[],2); % take max
crisp_out = sum(fuzzy_out .* (1:length(fuzzy_out))') ...
/ sum(fuzzy_out) - 11; % centroid
pobj(end,end).YData = fuzzy_out;
p3obj(1,4).Value = crisp_out;
% draw input values
[x1,~] = axesPosition2figurePosition(app,[fVal,1],ax(1,1));
xl = [x1 x1];
p3obj(1,1).X = xl;
[x1,~] = axesPosition2figurePosition(app,[nowIn,1],ax(1,2));
xl = [x1 x1];
p3obj(1,2).X = xl;
[x1,~] = axesPosition2figurePosition(app,[manIn,1],ax(1,3));
xl = [x1 x1];
p3obj(1,3).X = xl;
switch factor
case 1
t = 'Beauty Factor';
case 2
t = 'Power Factor';
case 3
t = 'Depth Factor';
otherwise
t = '';
end
sgtitle(fig, t);推論過程表示でサブグラフ横断のラインを引くのに、@michio_MWJ さんの axesPosition2figurePosition() を使用しています。
正式に annotation に入れてください! > MathWorks さん

各操作に対し、リアルタイムで推論過程が表示されます。
動作例
ファジィ・イコライザー動作
推論過程表示
推論過程表示は動作が重く音切れが発生するため音なしです。
バッファサイズを増やせば音切れしなくなりますが、レイテンシーが増えて表示とリンクしなくなるので・・。
スクリプト(AppDesigner)
あとがき
いかがでしたでしょうか?
言語化されたルールがあればすぐ適用でき、推論が軽いのが特徴です。
各プロダクション・ルールごとに独立なので、並列化してさらなる高速処理も可能で、エラーの影響も限定的です。
ルールに一部欠落、矛盾があっても動作し、システム全体の記述が困難な場合でも、局所ルールで全体を制御することもできます。
言語的な処理なので、エキスパートが持っているノウハウのルール化がしやすく、パラメータ調整・他の方法との組み合わせも容易です。
制御の一手段として検討してみる価値はあるかと思います。
一度おおはやりしてしまったので、なんか表立って「ファジィ理論使ってます!」って言いにくい感じもあるのかもしれませんが、多分そろそろその時代を知らない人達も増えてきてると思うので、今一度・・。
人工知能ブームも過去に何度かありましたし、ファジィ理論も AI といえば AI ですし!
参考文献
(1)ファジィシステム入門 寺野、浅居、菅野 オーム社
(2)ファジィ理論とその応用 水本 サイエンス社
(3)ファジィ制御 菅野 日刊工業新聞社
(4)FUZZYコンピュータの発想 山川 講談社
(5)「ファジィ制御技術」 西島 他 東芝
東芝レビュー(43巻4号) pp299-326
(6)「実用期に入ったファジィ理論」 稲葉 他 日経マグロウヒル社
日経エレクトロニクス 7-27 (No.426) pp130-152 1987
(7)音色の研究Ⅱ-再生音の音質に関する因子的研究 三戸、北村、難波、松本 音響学会講演論文集 pp55-56 (May 1961)
(8)音の評価に使われることばの分析 曽根、城戸、二村 音響学会誌 18 pp320-326 (1962)
The title image was created using Adobe Generative Fill based on this picture.

