サンプリング・レート・コンバーター～マルチステージ化・ポリフェーズ化で演算量を大幅削減！～マルチレート信号処理とは？

前の記事「折り返し雑音とは？～なぜ車のホイールは逆回転するのか～デジタルはアナログの近似ではない」で、「デジタル信号処理にとってサンプリングレートの変換は苦手な処理」であるが「マルチステージフィルターやポリフェーズフィルターを駆使すれば、比較的少ない演算量で原理通りの処理を行い、音質変化のほとんどない変換を行うことは可能」ということを述べました。

今回はその、「マルチステージフィルター」と「ポリフェーズフィルター」を用いた「サンプリングレートコンバーター」の説明をしたいと思います。

この「マルチレート信号処理」と呼ばれる技術は応用範囲も広いので、マスターしておいて損はないと思います。(-_☆)

１ サンプリング・レート変換

１-１　アナログ方式とデジタル方式

１-１-１　アナログ方式
サンプリングレート変換の最も簡単な方法は、一旦D/A変換を行ってアナログ信号とし、それを希望する新たなサンプリング周波数でA/D変換し直すことです。しかしこの方法はアナログ信号を介すため、当然、ノイズやジッター等の問題で音質劣化・変化は避けられません。したがってアナログ信号を介さない、オールデジタルの処理が望まれます。

１-１-２　デジタル方式
原理的には、サンプリング周波数を fa(Hz) から fb(Hz) に変換するには、一旦サンプル点を fa と fb の最小公倍数に増やしその後サンプル点を間引くことで達成できます。しかしこれらの処理を単純に行うと、折り返し雑音の記事でも説明したように折り返しノイズの発生があり得ます。したがって処理過程でサンプリング定理を満たしているか、変換後に折り返しノイズが相殺されること（QMF、TDAC等）が必要となります。さらにこの処理を高精度に行うには膨大な量の演算が必要となるため、ハードウェアや、ソフトでのリアルタイム変換には演算量を減らす工夫が必要となります。

１-２　デジタルレート変換

ここでは実際の例として、3/2及び2/3にレート変換する場合を取り上げ説明します。まず3/2にレート変換する場合の手順を以下に、このときのスペクトル変化の様子をFig. １-１に示します。

　①サンプル点の間に2個の0点を挿入し、サンプリング周波数を3倍に引き上げる
　　元の信号のスペクトルを(a)とすると、ｚ変換とフーリエ変換の関係から0点挿入後のスペクトルは(b)のようになる
　②①で発生したイメージ成分を、1/3帯域のLPFによって取り除く
　　0点挿入の段階で信号のDCレベルは1/3に落ちているので、このLPFのDCゲインは3とする
　③2個に1個のデータを取りだし、サンプル点を1/2に間引く
　　スペクトルは(e)のようになり、レート変換が終了する

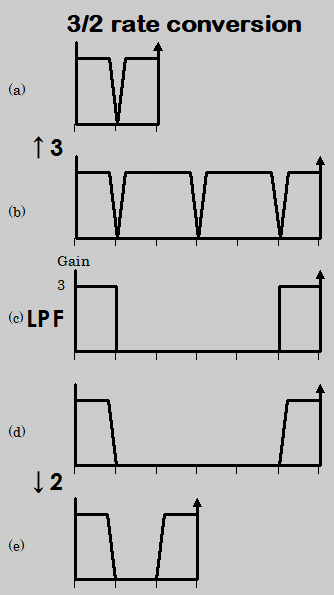
Fig. １-１　3/2　レート変換

次に2/3にレート変換する場合の手順を以下に、このときのスペクトル変化の様子を Fig. １-２に示します。
　①サンプル点の間に1個の0点を挿入し、サンプリング周波数を2倍に引き上げる
　②①で発生したイメージ成分を、間引き後に折り返し雑音の発生がないよう、1/3帯域のLPFによって取り除く
　0点挿入の段階で信号のDCレベルは1/2に下がっているので、このLPFのDCゲインは2とする
　③3個に1個のデータを取りだし、サンプル点を1/3に間引く
　　スペクトルは(e)のようになり、レート変換が終了する

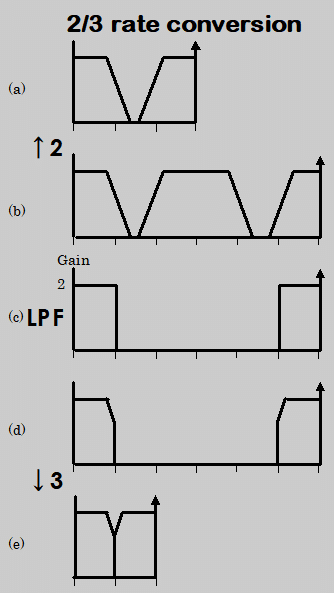
Fig. １-２　2/3　レート変換

つまり、一般的には以下の手順で行えばよいことになります。
L/Mにレート変換行うとすると、
①サンプル点の間にL-1個の0点を挿入し、サンプリング周波数をL倍に引き上げる
②①で発生したイメージ成分を、間引き後に折り返し雑音の発生がないよう、1/L、または1/Mの帯域が狭い方のLPFによって取り除く
　0点挿入の段階で信号のDCレベルは1/Ｌに落ちているので、このLPFのDCゲインはLとする
③M個に1個のデータを取りだし、サンプル点を1/Mに間引く
　したがって変換フィルタは、L/Mの場合とM/Lの場合では、DCゲインが異なるだけでカットオフ周波数は同じである

折り返し雑音の記事でも説明したように、デジタル信号のスペクトルは無限に繰り返されます。したがって、アップサンプリングにおいても上記LPFによってそのイメージ成分を取り除く必要があることに注意してください。

「理想LPFでイメージ成分を取り除く」のは、これも折り返し雑音の記事で説明したように、時間軸では sinc関数でデータ補間するのと同意です。他の演算量の軽い補間関数を用いる方法もありますが、当然信号の減衰や折り返し雑音が発生し、「高音質」を求めるのであればお勧めはできません。

１-３　同期／非同期、直接／間接変換

１-３-１ 同期式直接変換

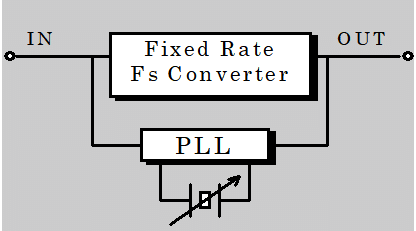
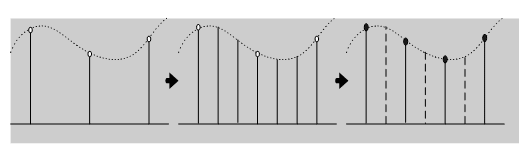
Fig. １-３　同期式直接変換

原理通りに行うのが、この同期式直接変換です。Fig. １-３の例ではサンプリング周波数を3/2に変換するために、一旦サンプル点を３倍に増やしそれを１つおきに間引いてレート変換を行っています。この方法では入出力のクロックを同期させるPLLが必要となります。しかし変換比は固定であり、変換部のLPFの精度が変換精度を決定します。そのため、変換精度が入力信号のタイムジッターなどに影響されることはありません。ハードウェアにおいても、一旦コンピュータなどに取り込んで変換するのと同じ処理が行えます。

例として、デジタルオーディオでよく用いられる 44.1/48/88.2/96kHz での変換比を Table １-１に示します。

Table １-１　変換比

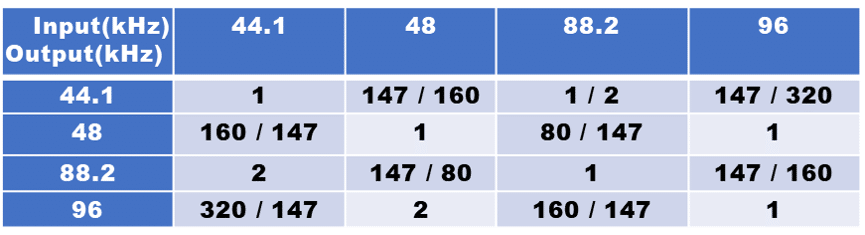
この表から分かるように、原理通りに行うには最高320倍オーバーサンプリング上でフィルタリングを行う必要があります。しかもそのフィルタに必要なタップ数は、24ビット精度を得るには数千～数万タップにもなります。

１-３-２ 非同期式間接変換

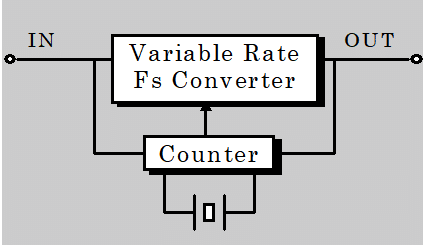
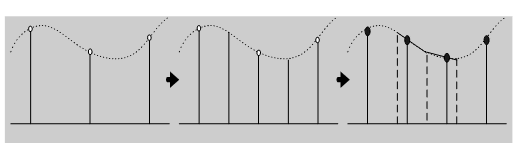
Fig. １-４　非同期式間接変換

同期式直接変換では、１種類の変換レートでも膨大な演算量を必要とします。さらに、複数の変換レートに対応するハードウェアの実現はかなりの困難を伴います。また、ビデオレートとの変換等入出力が非同期で変換を行う要求もあり、市場に出ているレートコンバータハードウェアの多くが非同期式を採用しています。

非同期式では、出力は目的とする固定の周波数であり、これに対する入力周波数を何らかの方法で測定して、変換比をアダプティブに変更します。変換比がバリアブルであるため、当然全ての変換フィルタを持つことはできません。そのため多くの場合、以下のような手順で変換を行います。

①処理が簡単な２の乗数倍(数百倍程度)でオーバーサンプリングする。
②入力周波数を出力周波数でカウントし、平均等の処理を行って変換比を決定する。
③決定された変換比に従い必要なサンプリング点のデータを、その周辺のデータから直線補間等の簡単な処理で算出する。

Fig. １-４の例では同期式と同じ3/2にサンプリング周波数を変換するのに、一旦２倍にオーバーサンプリングし、それらのデータを用いて直線補間で必要なデータを算出しています。

この方法ではPLLも不要であり、前段のオーバーサンプリングはすでにあるオーバーサンプリングICなども利用できます。したがってハードウェアでの実現性は高く、IC化も比較的容易です。

またジッターのある入力でも変換比を変えて対応するため、結果的に出力のクロック精度を上げることができ、ジッターリデューサーとしての機能も合わせ持ちます。しかしこれはA/D、D/Aの組合せでは有効ですが、D/Dでは以下のような問題が発生します。

①変換精度を上げるには、前段のオーバーサンプリングの段数を上げる必要がある。20ビット精度程度を得るのにも最低数百倍のオーバーサンプリングが必要であり、それ以上精度を上げるとハードウェアの規模が増大する
②変換比を変えることによってジッターや絶対偏差を吸収しているため、原信号と周波数成分が変わってしまい音質変化は避けられない
③変換比を入出力クロックから算出するため、特にジッターのあるソースに対してその精度が問題となる

Fig. １-５とFig. １-６に、CDから再生した10.007kHzの正弦波を、それぞれ非同期式と同期式で48kHzサンプリングに変換した場合のスペクトルを示します。

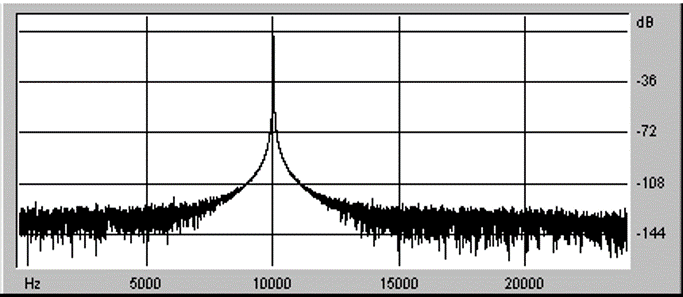
Fig. １-５ 非同期式変換結果 

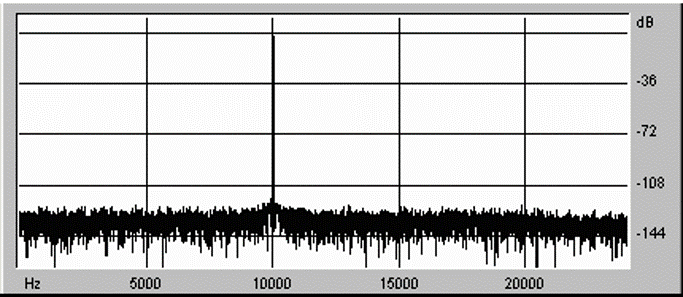
Fig. １-６　同期式変換結果

非同期式ではCDからの入力に対しても変換後のスペクトルは時間とともに変動し、メインローブが広がってしまっています。同期式ではこのようなことは起りません。

したがって高精度な変換（＝変換前後で音質変化がほとんどない）を目的とするならば、同期式で、しかも直接変換を行う必要があります。

２ マルチレート・デジタル信号処理

前述したように、マルチレートの信号処理では多くの演算量が必要となります。しかしシステムに適合したテクニックを利用することにより、演算量を削減できます。ここではその代表的なものを説明します。

２-１ マルチステージ・フィルタ１

レートコンバージョンにおけるインターポレーションレートあるいはデシメーションレートの少なくとも一方が大きい数の場合、コンバージョンフィルタを多段に分割することによりフィルタのタップ数を減らせる可能性があります。ここでは、44.1kHz→48kHzサンプリングレート変換を、シングルステージで行う場合及びマルチステージでの１つの実現例について説明します。

１-２でふれたように、44.1kHz→48kHzサンプリングレート変換を行うには以下のようにします。
　①サンプリング周波数を44.1と48の公倍にするために、160倍オーバーサンプリングを行う
　②急峻な遮断特性を持つフィルタで、160倍オーバーサンプリング上でイメージ成分を取り除く
　③1/147にデシメーションする

この場合、②のフィルタリングに必要な演算量を試算してみましょう。
等リップルフィルタのタップ数Ｎは、以下の式で与えられることが知られています。

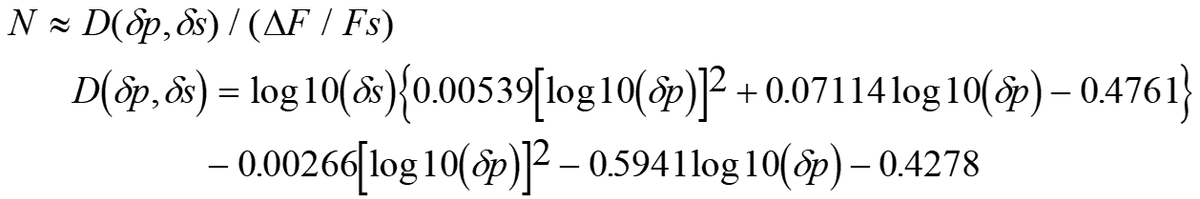
δp：パスバンドリップル
δs：ストップバンドリップル
ΔF：トランジットバンド幅
Fs：サンプリング周波数

今、例えば以下ようなかなり厳しい条件でフィルタ設計を行うとします。
　　　　δp = -150dB, δs = -150dB, ΔF = 2kHz
するとシングルステージの場合に必要なフィルタのタップ数Ｎsは、
　　　　Ｎs = 32377 (Fs=160×44.1kHz)
となります。

ここで、1/147の部分を1/49と1/3にマルチステージ化してみましょう。

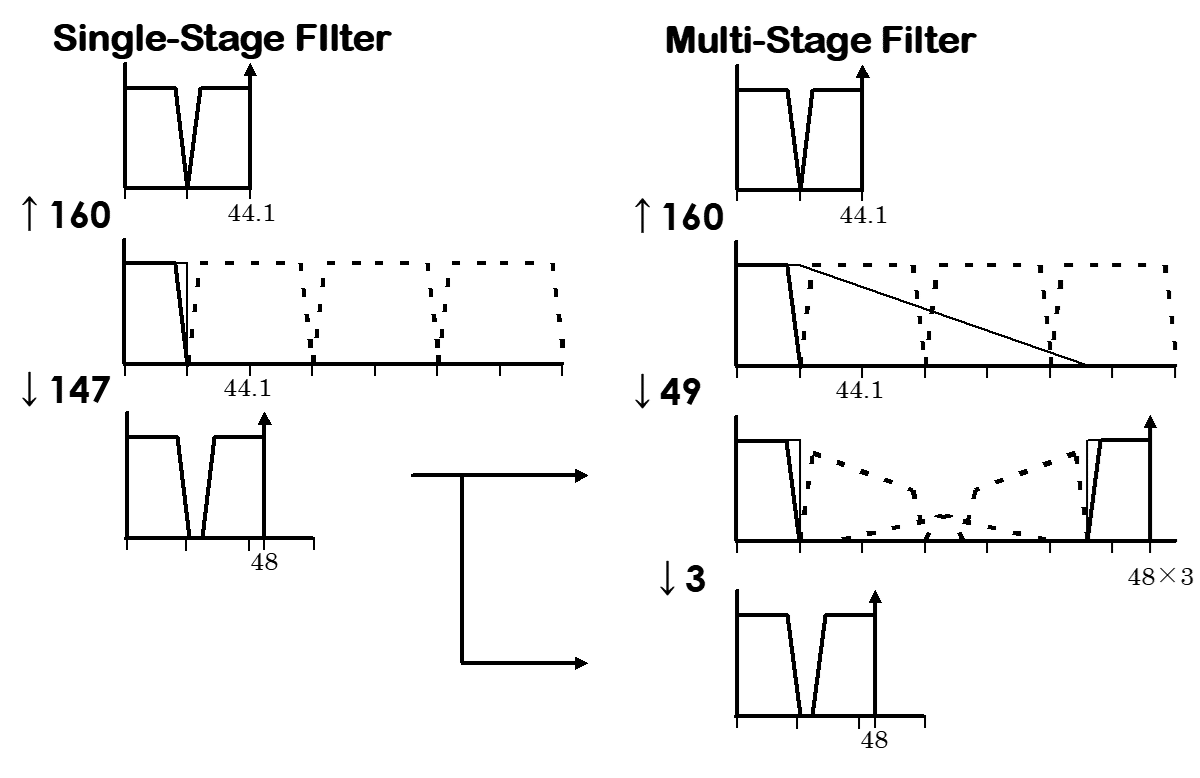
Fig. ２-１　マルチステージフィルタ 1

この場合、1/49にデシメーションした段階では最終的には不要な、(44.1/2) kHz ～ (48×3-44.1/2) kHz の部分が存在します。この帯域は後で取り除けば、この段階では折り返し雑音があっても良いことになります。したがってシングルステージのように急峻なフィルタは必要なく、Fig. ２-１右側に示してあるような緩やかな遮断特性のフィルタでかまいません。つまり、高い周波数段階では緩やかな(タップ数の少ない=演算量の少ない)フィルタを用い、周波数が低くなったところで急峻なフィルタで折り返し雑音を取り除いてやればよいのです。この場合のフィルタは、例えば以下の条件で設計します。

　　　　1st：δp = -156dB, δs = -150dB, ΔF = (48×3-44.1)kHz
　　　　2nd：δp = -156dB, δs = -150dB, ΔF = 2kHz

　＊多段接続の場合、総合特性のリップルは各ステージの掛け算になることに注意。そのため各ステージのパスバンドリップルはその分小さい必要があります。ストップバンドリップルは抑圧方向なのでそのままでOKです。

したがって各ステージで必要な各フィルタのタップ数Ｎm1、Ｎm2は、
　　　　Ｎm1 = 656 (Fs=160×44.1kHz)
　　　　Ｎm2 = 671 (Fs=3×48kHz)
となり、シングルステージの場合の 32377 タップに比べ、大幅に演算量が削減されます。

MATLABには dsp.SampleRateConverter 関数があってマルチステージ・ポリフェーズフィルター化もしてくれるのですが、それは変換比が大きい場合であって、上記のような初段で折り返しを許容するようなアルゴリズムは搭載されていないようです。

２-２ マルチステージ・フィルタ２

1と同様にインターポレーションレートあるいはデシメーションレートが大きい場合、フィルタを多段に分割することによりさらにフィルタのタップ数を減らせる可能性があります。

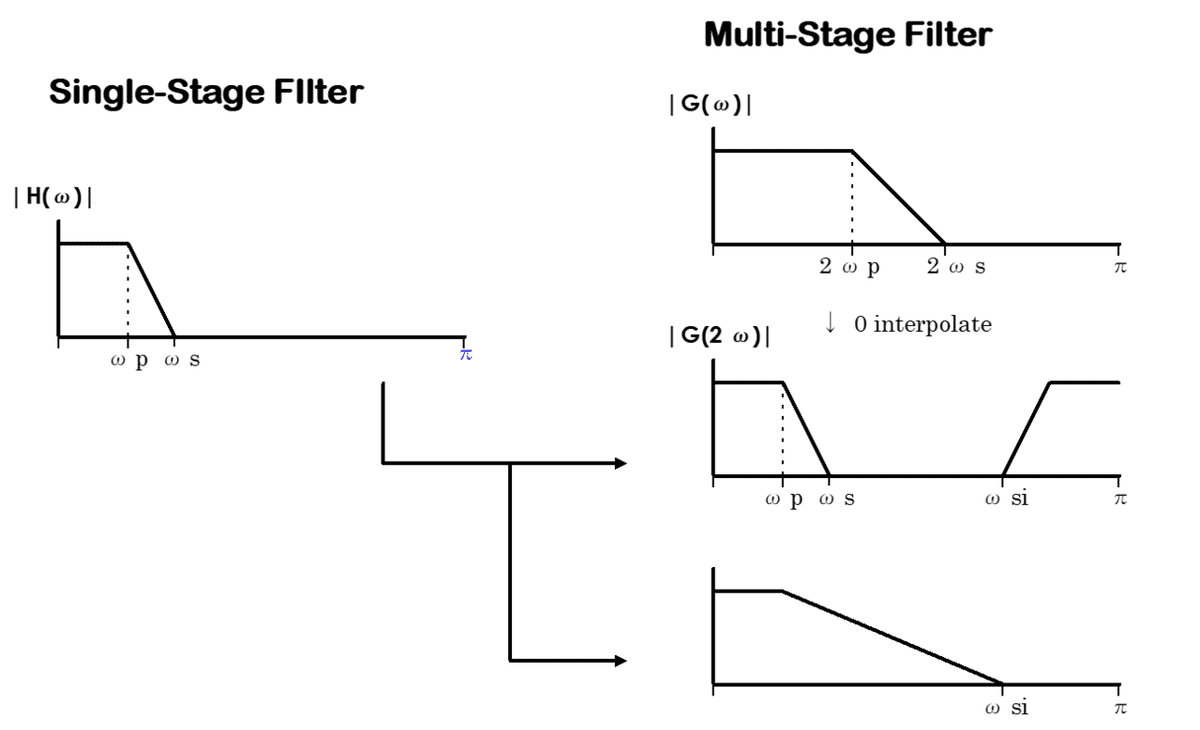
Fig. ２-２　マルチステージフィルタ 2

今、1/2のデシメーションの場合を考えます。
デシメーションフィルタの特性をFig. ２-２左図(ωs＜π/2)とすると、まずその目的の特性を周波数上で２倍に伸ばしたフィルタ(右上段)を設計します。するとそのタップ数は目的のフィルタの半分で済みます。このフィルタ係数に１つおきに０点を挿入すると、z変換と周波数特性の関係から明らかなように特性は右中段のようになります。したがってこのフィルタと右下段のフィルタを縦続接続することにより、目的の特性が得られます。

この手法はωs ＜ π／２でなければ使えませんが、インターポレーション／デシメーションレートが高ければ高いほど(ωs がπ/2に対して低ければ低いときほど)フィルタのタップ数を減らすことができます。元のフィルタのタップ数をＮ、インターポレーション(デシメーション)レートをｎ、マルチステージフィルタの各タップ数をＮm1、Ｎm2とすると、
　　　　Ｎm1=Ｎ/ｎ，　Ｎm2＝Ｎ×{(ωs-ωp)/(ωsi-ωp)}
の関係があります。したがって、ｎ=2程度のときはメリットが少ないですが、例えばｎ=20では演算量が1/10以下になります。

マルチステージ化のメリットは、単に演算量／メモリ量の低減ばかりではありません。フィルタのタップ数が削減できることによりフィルタ設計の簡易化が図れ、有限演算長による演算誤差の問題も軽減できます。

２-３ ポリフェーズ・フィルタ

原理では、一旦 L 倍にインターポレーションを行い、その後 1/M にデシメーションを行うことにより L/M のレート変換を行うと述べました。しかしこの方法では、最終的に必要なレートは L/M 倍であるにもかかわらず、途中で L 倍のレートのデータが発生しています。そこでFig. １-１を、Fig. ２-３ に示すように時間軸での処理に書き直してみます。その過程を見ると、以下の２点の無駄な演算が存在することが分かります。

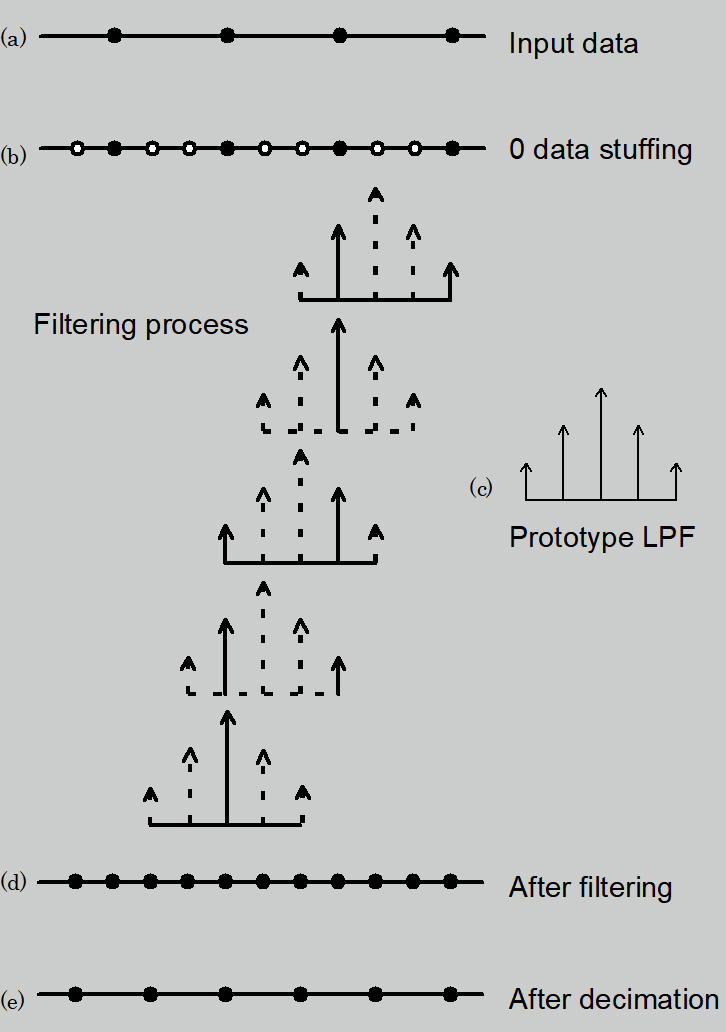
Fig. ２-３　ポリフェーズフィルタ

①（ｂ）から（ｄ）のデータを算出するフィルタリングにおいて、元データの３つに２つは０であるため、３つに１つしか演算する必要はない。つまり、（ｄ）の１つのデータを算出するのに必要なフィルタ係数は、（ｃ）のフィルタ係数の、３つに１つである
②（ｄ）から（ｅ）で、２つに１つはデータを捨ててしまう。したがって、最終的に捨てられるデータを算出する演算は、元々行う必要がない

以上の無駄な操作を取り除いたのがポリフェーズフィルタです。
元々のフィルタ係数の（Ｌ－１）個おきの係数を採ってＬ組のフィルタを作り（この操作をポリフェーズ分解と呼びます）、これらを切り替えることにより（フィルタの畳み込み演算器のメモリは共通で、係数器だけを切り替えれば良い）、一旦Ｌ倍にレートを上げることなく（ａ）から（ｅ）のデータを直接算出することができます。

これにより、以下のようなメリットがあります。

①ソフトウェアにおいては、演算スピードが上がり、ハードウェアにおいてはクロック周波数が低くても良い
②ソフト、ハードともに、多くのメモリを必要としない

Fig. ２-４ とFig. ２-５ に、それぞれ3/2、2/3変換の場合のポリフェーズ分解の様子を示します。

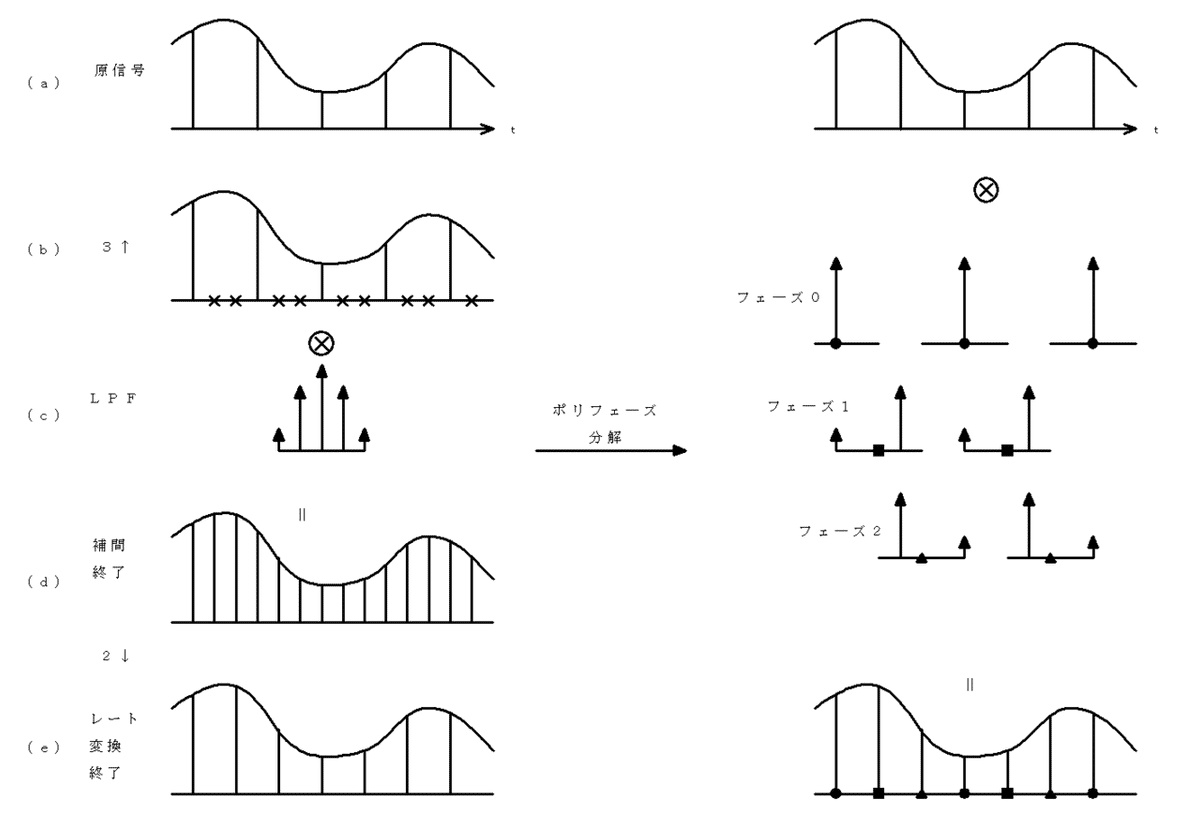
Fig. ２-４　3/2変換ポリフェーズ分解

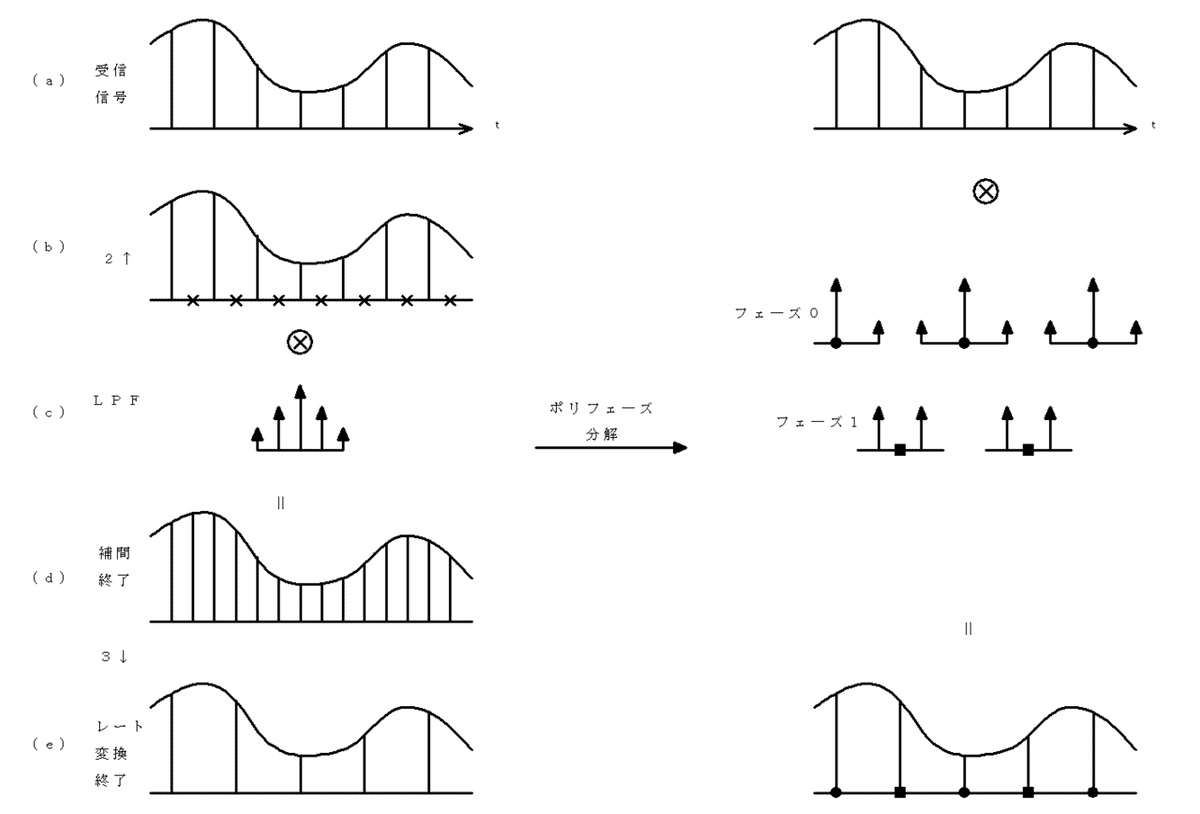
Fig. ２-５　2/3変換ポリフェーズ分解

MATLABでは dsp.FIRHalfbandInterpolator/dsp.FIRHalfbandDecimator 関数でポリフェーズ・フィルターが簡単に設計できます。
さらに dsp.IIRHalfbandInterpolator/dsp.IIRHalfbandDecimator もあるので、IIRフィルターのポリフェーズ化も一発です！

２-４ ポリフェーズフィルタの数式表現

次にポリフェーズフィルタを一般化するため、数式での表現を考えます。
まず、以下のようなサンプリングレート変換システムを考えましょう｡

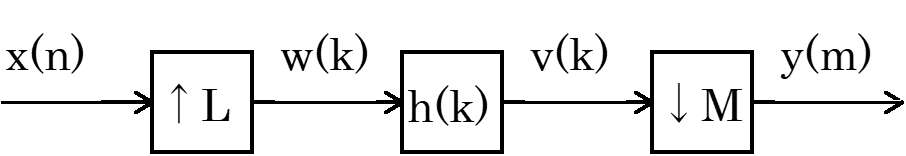
　　　　　　　　　　　　*h(k)は変換フィルタのインパルス応答

Fig. ２-６　サンプリングレート変換システム

この時､各信号の関係は以下のようになります。

v(k) は w(k) と h(k) のコンボルーションなので、

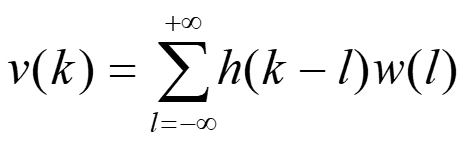
Eq. 1

w(k) は、x(n) のサンプル点の間に L-1 個の0点を挿入したものなので、r を整数とすると、

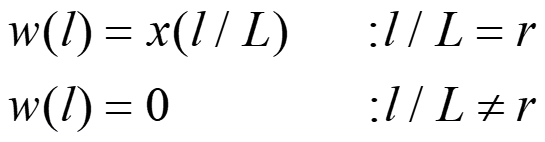
Eq. 2

よって v(k) は、

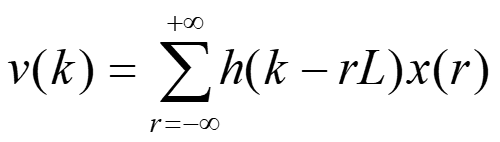
Eq. 3

 と表されます。また y(m) は、v(k) をMサンプルに1つとったものなので、

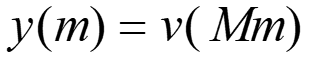
Eq. 4

よって、入出力の関係は次式で与えられます。

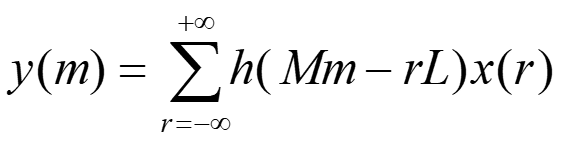
Eq. 5

ここで、入出力のインデックス関係を明らかにするために､ Eq.2, 4から、

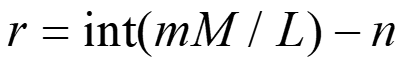
Eq. 6

とおきます。するとEq.5は以下のようになります。

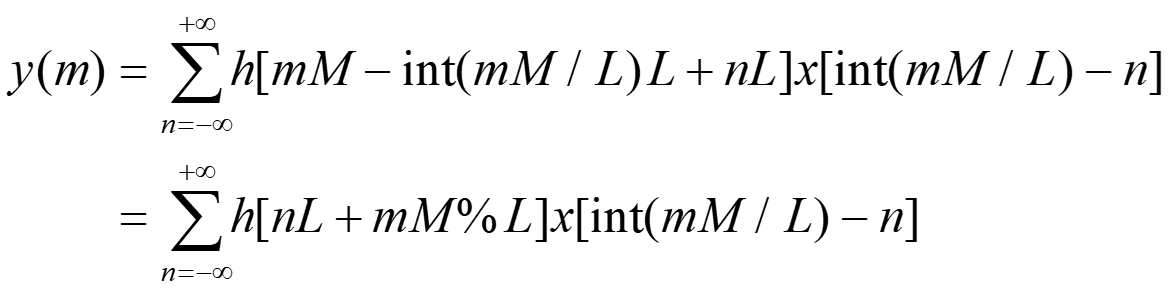
Eq. 7

このとき、 h[nL + mM%L] は各フェーズの係数組を表しており､それらを

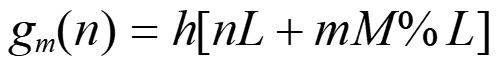
Eq. 8

とおけば、

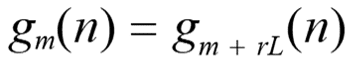
 : r = 0, ±1, ±2, ...

Eq. 9

の関係があります｡

さらに、プロトタイプフィルタのタップ数 N を、L の整数倍、N=QL とすると、

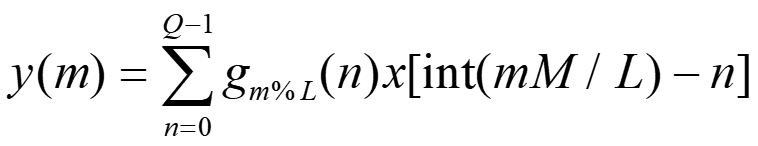
Eq. 10

となります。

Qは各フェーズのフィルタのタップ数です。

これより、ｍ が 0 ～ L-1 で入出力関係が一巡し､その時入力ポインタは 0 ～ M-1 まで進むことが分かります｡つまり､Mサンプルの新規入力データから､Lサンプルのデータが出力され、ブロックごとの演算が可能である事を示しています｡したがって、入力バッファとして “M+Q-1” の長さがあれば、1出力サンプル毎に 

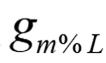
の係数組を用いてコンボルーションを行い、L サンプルの出力を発生することができるということになります。

以下に、L=3, M=2 の場合の実際のポインタの値と、その演算に “M+Q-1” の容量のリングバッファを適用した例を示します。

この表から、3サンプルの出力を得るためには2サンプルの新規入力データが必要であり、その間、3組の係数組が用いられることが分かります。

L=3,M=2 の例

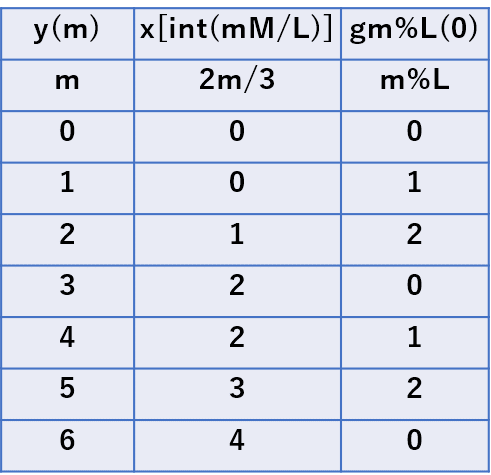
リングバッファを用いれば、以下のような手順で効率的に演算が行えます。
　　①バッファ内容を0で初期化；ポインタ=0
　　②2サンプル読み込み
　　③以下を演算

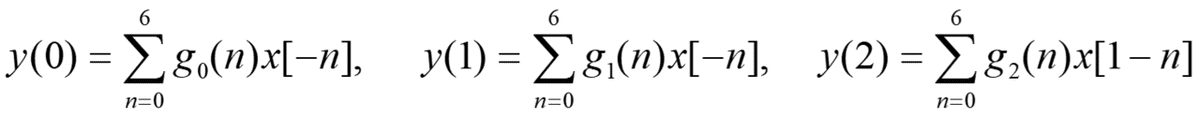
　　④先頭ポインタを + 2移動
　　⑤②～④を繰り返し

リングバッファ使用例

このように、原理からすれば入出力の周波数が近い場合は多くの演算量が要求されることになりますが、その分はポリフェーズ化によって削減ができます。つまりどのような変換比であっても、入出力レート以上に演算レートを上げることなくレート変換を行うことができます。

最初にも書きましたが、今回説明したマルチステージ・フィルターとポリフェーズ・フィルターは応用範囲も広いので、機会があれば検討してみてはいかがでしょうか？