比例代表選挙における議席数の割り振り方
目的
比例代表の議席振り分けのようにできるだけ平等に議席を振り分ける処理をプログラムで実現したい。
そのためにどのような振り分け方法があるのか調査し、プログラムに落とし込めるかを確認したい。
課題感
得票率に応じてそのまま議席を分けると小数点以下が発生してしまう。
議席など少数点以下で振り分けられないものがある。
少数点以下で振り分けられるものであっても少数点の切り捨てによって「割振る数」と「割り振られた数」合計値が一致しなくなる。
結論
ヘアー式またはドループ式の基数の除算による整数部分を処理する。
割振り切れなかった議席については除算の余りを「ハ-ゲン・ビショップ方式」(実質ドント式)で処理して割り振る。
ドント式(最高平均方式)
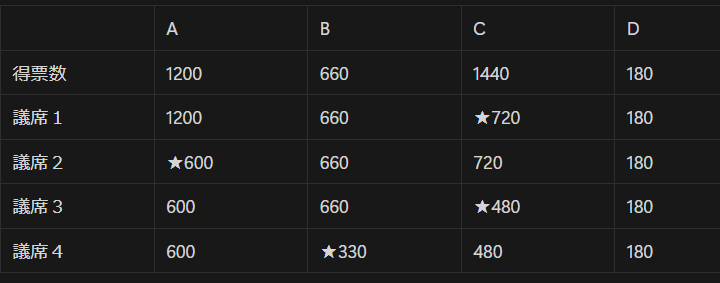
各党の得票数を割っていってその数が多いものから議席を配分していく。

上記の表のようにすべての数で割った表を作ってから議席を配分しなくても、1議席ごと得票数Maxに割り振って、その党の得票数を除算していけばプログラム処理は可能。
※Maxが複数党で同じ票の場合どうするかなどの問題は出てくる。
後述するドループ方式で整数表を割り振ったのちにあまりの議席を「ハ-ゲン・ビショップ方式」で割り振るという方法でも同じ結果が期待できる。(参考)
1議席ごと処理をする必要がない分こちらの方がプログラム処理に向いていそう。

[各政党の獲得票数]÷[各政党の獲得議席数+1(,2,3,4……)]で割っていき、最大の数を出した政党に1議席。さらに1議席足りない場合は2番目の数を持っている政党に1議席分配される。
※あまり部分だけをドント式で処理しているイメージ
課題
議席数が多くなると処理が重くなる。
追記
ドント式では議席を割り振ると2,3,4と一つずつ除数を増やしていく。3,5,7と2つずつ除数を増やして議席を割り振っていくと少数政党にも議席が割り振られるようになる。しかし得票率による配分からは乖離する。(政治における少数意見を反映するというような意図がない限りは取り入れる必要なさそう)
ヘアー式(最大剰余方式)
投票総数を議員定数で割った数の整数部分を「ヘアー基数」とする
獲得票数をヘアー基数で割る
あまりの大きい順に議席のあまりを振り分ける

課題
小数部分を切り上げるか切り捨てるか
パラドックスが発生する
端数処理の単純さが原因
ドループ式
基数を定義して議席を割り振る部分は同じ。
議席1について争う場合、1議席獲得に十分な票数の割合は2分の1以上となる。議席2の場合は3分の1超、議席3の場合は4分の1超となる。ということは、x議席獲得のための十分条件は[投票総数]÷[議席数+1]+1となる(小数点は四捨五入などする)。これがドループ基数。

課題
ヘアー式に同じ
