熱力学ミニマム
はじめに
ここでは、清水熱力学流の展開はせず、平凡な展開の仕方で、最低限の内容をまとめる。どちらかというと復習用の記事。
じきに清水流の展開についてもまとめる予定である。
熱力学の適用範囲
熱力学は、微粒子の運動を追うようなことはせず、マクロに見て言えることを言う。特に、マクロに見て時間変化しないような状態、すなわち、平衡状態だけを扱う。
何かの変化を語るときは、平衡な始状態と平衡に達した終状態の2状態にだけフォーカスして、その途中経過を語ることはない。
もし途中経過を知りたければ、分子動力学や反応速度論の力を借りる必要がある。
マクロな物理量
熱力学において扱う量は、
圧力Pや体積V, 仕事W
温度TやエントロピーS, 熱Q
内部エネルギーU, エントロピーH, ヘルムホルツエネルギーF, ギブズエネルギーG
などのマクロな物理量である。※
このなかで、QとWだけは経路に依る量(経路関数)であり、その他の量は経路には依らず状態に対して一意な状態量(状態関数)である。
このことには留意しておく必要がある。
また、示量変数(質量を倍にしたら倍になる量)と示強変数(倍にならず不変)の違いについても留意しておくとよい。
※ 容器の形や束縛条件、変化の度合いを示す比熱、磁化率などには言及しない。
アウトライン
熱力学の根幹をなすのは、熱力学第一法則(エネルギー保存則)と熱力学第二法則(自発変化の方向性)であると思う。第零や第三法則は略す。
具体的なことは、「系の種類」と「状態変化の過程の種類」、「系の成分や相」を指定すれば自動的に導ける。※
原理的に取り出し得る最大の仕事量を求められるのは熱力学の魅力のひとつ。
また、数学的操作である全微分の式と比較することで、マクロ量同士の関係性が見えてくる。
系の種類:孤立系、閉鎖系、開放系
状態変化の過程1:定圧p、定容v、等温t、断熱q、等温定圧など。
状態変化の過程2:可逆、準静的、不可逆など。
系の成分:理想気体、光子気体など。
系の相:固相、液相、気相、…。
※ なお、しばらく、1相1成分で、どこをとっても均質均一な状態を想定して構わない。重力や電場などの外力は想定しなくてよい。
基本法則
<熱力学第一法則>
熱力学第一法則とは、エネルギー保存則のことであり、暗に熱と仕事の等価性を言っている。どちらも単位はジュール [ J ]である。
dU=δQ+δW
内部エネルギーは状態関数であるが、QとWは経路関数である。
Qの具体形は、比熱×温度の積分あるいは、エントロピー×温度の積分という状態量で表せることもある。
Wの具体形は、圧力×体積の積分で表せる。(ただし膨張仕事を想定)
・余談1
熱力学第一法則に反して、外から加えた熱量以上の仕事を外にできるというありえない熱機関のことを第一種永久機関という。
・余談2
理想気体において、温度一定なら体積変化しても内部エネルギーは変化しない。(ジュールの法則)
・余談3
理想気体に対して、$${C_p-C_v=RT}$$(マイヤーの関係式)
・余談4
理想気体の断熱過程において、$${pV^γ=const}$$(ポアッソンの
の法則)
ただし、$${γ=\frac{C_p}{C_v}}$$
<熱力学第二法則>
熱力学第二法則は、熱の流れの不可逆性を言っている。
この法則は定性的に、
クラウジウスの原理「ほかに何の変化を残すこともなく、熱を低温側から高温側に移すことはできない」
トムソンの原理「一つだけの熱源を利用して、その熱源から熱を取り入れ、それを全部仕事に変えるような熱機関はあり得ない」
という同値な原理によって言い表されている。
ここでは、エントロピーという量が表立ってはいない。
証明は省くが、カルノーの定理が「カルノーサイクルにおいて効率は、作業物質の種類に依らず、高温・低温の温度によってのみ決まる」ことを保障しているので、物質の種類に依らない普遍的な温度スケールをカルノーサイクルを拠り所にして(理想気体からT=0を決めることで)確定させられる。この温度を熱力学的絶対温度という。水の凝固点と沸点とを100等分した経験温度とは概念が異なる。(清水熱力学では定義の仕方がまた異なる。)
カルノーサイクルでは、得た熱Q1と放出した熱Q2は(した仕事Wのぶんだけ)等しくないが、これらを熱力学的絶対温度で割った量は等しくなる。
(Q1/T1=Q2/T2)この保存量つまり状態量をエントロピーSという。
より一般の準静的サイクルにおいてもエントロピーは保存量となる。
このことは、微小なカルノーサイクルの積み重ねで一般の準静的サイクルを模すことで証明できる。
また、エントロピーが経路に依存しないことは、地点AとBと全く異なる経路で結んで、積分範囲を逆転させることによって証明できる。
このようにして、状態量としてのエントロピーを、カルノーサイクルに限らず、より一般に扱うことできるようになる。
熱力学第二法則は、エントロピー増大則とも混同されるが、エントロピー増大則が言えるのは、あくまで孤立系(閉鎖系+断熱過程)の場合である。
エントロピー増大則とは「孤立系のエントロピーは不可逆過程によって常に増大する」という原則である。
このことは、一般のサイクルにおけるクラウジウスの不等式を可逆経路と不可逆経路のなす閉じた経路に適用することで導かれる。
カルノーサイクルにおいては、カルノーの第二定理「不可逆機関の効率は可逆なカルノー機関の効率よりも悪い」と言い当てられている。
もらった熱量が、仕事のほかに、エントロピー生成に使用されてしまうことが非効率の原因である。
内部エネルギーのうち自由に使えるエネルギーは、膨張仕事や自由エネルギーと言われ、そうでないものを束縛エネルギーという。
<系の自発変化の方向>
孤立系(閉鎖系+断熱過程):dS ≥ 0(エントロピー増大則)
等温等積過程(閉鎖系の一種):dF ≤ 0
等温等圧過程(開放系でもよい):dG ≤ 0(化学でよく使う)
<熱力学変数同士の関係>
これら変数の関係は、この画像で覚えやすい。
覚えなくとも、熱力学第一法則を起点として、状態変化の過程に基づく状態関数の形を書き表せば、自然な変数が何かわかる。
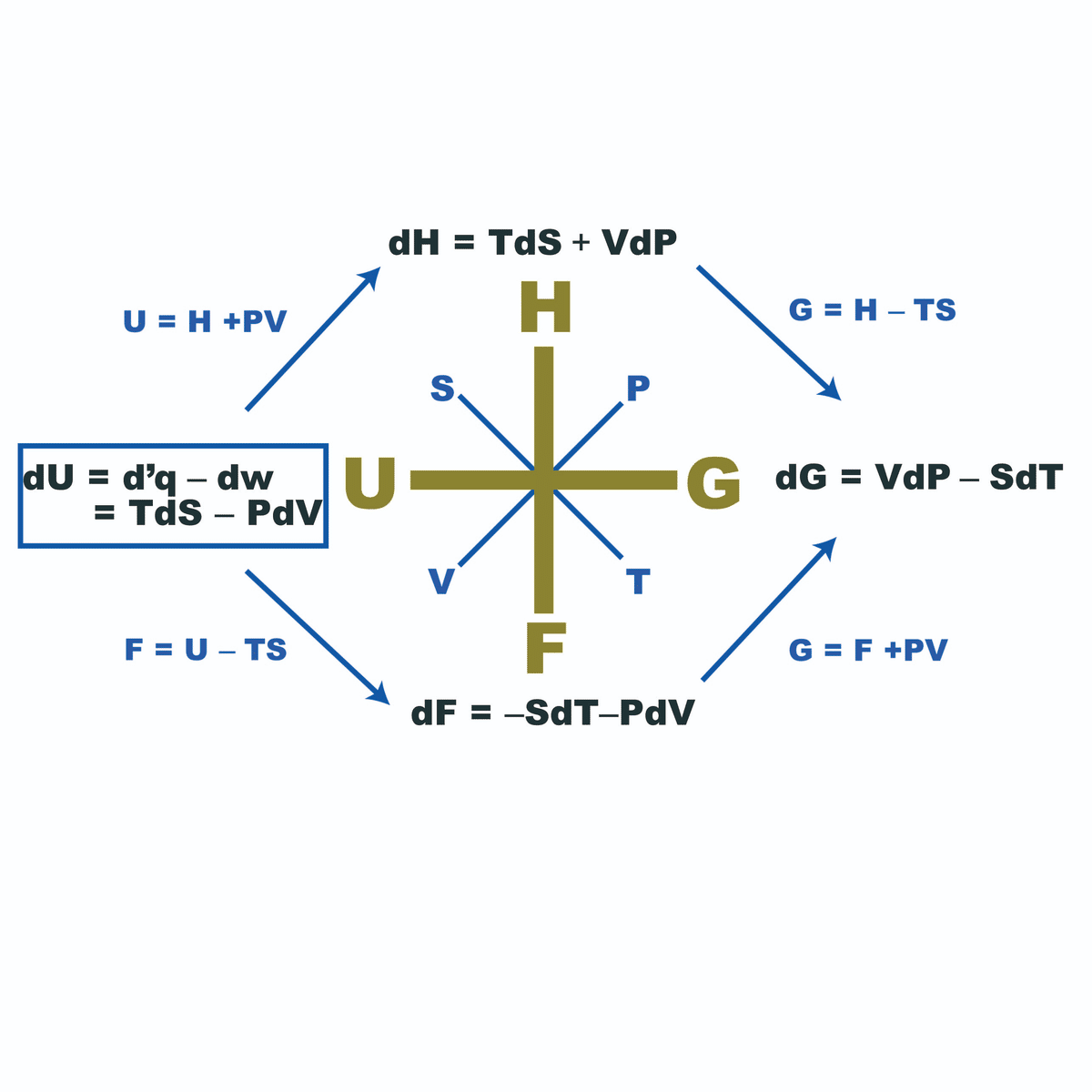
これと全微分の式と比較すれば、以下のマクスウェルの関係式が導ける。

右下4つの偏微分同士の等式がマクスウェルの関係式である。
左辺と右辺の一方どちらかは、測定しやすい量となっている。
例えば、Sは直接測定しにくいが、TやVやPはしやすい。
このように、マクスウェルの関係式は、直接測定しにくい量を、しやすい量で置き換えられることを言っている。
<熱力学の応用>
ここまでで、基礎的な熱力学の話はできたつもりでいる。
あとは、これらを用いて化学などで便利な式を導くことができる。
しかし、いちいち式やその導出を書くのは面倒なので、紹介にとどめる。
ギブズ・ヘルムホルツの式(ΔHから任意の温度のΔGがわかる。ΔHはキルヒホッフの式とHessの法則から求めておく。)
平衡定数と自由エネルギー差の式(自由エネルギーから平衡定数がわかる。)
ファント・ホッフの式(平衡定数の温度依存性がわかる。)
クラペイロンの式(相図をかける。境界の傾きがわかる。)
クラウジウス・クラペイロンの式(蒸気圧から蒸発熱がわかる。)
ギブズの相律(成分数と相数と自由度。相図をかける。)
ラウールの法則(モル分率と分圧の関係:高濃度極限)
ヘンリーの法則(モル分率と分圧の関係:低濃度極限)
沸点上昇
凝固点降下
浸透圧
ネルンストの式(標準電極電位と標準ギブズエネルギーと平衡定数の関係、無機化学でも大事。)
以上。2023/08/15バージョン。
間違いや質問があったらコメントしてください。
この記事が気に入ったらサポートをしてみませんか?
