債権法改正―法定利率と市場金利の逆転・マイナス法定利率
◆ SUMMARY ◆
改正民法における変動法定利率の下では、理論上、法定利率と市場金利(市中金利)の逆転が起こり得るし、また、法定利率がマイナスになり得る。
◆ 検 討 ◆
ジュリスト2018年1月号(No. 1514)(以下「本ジュリスト」といいます。)掲載の「連載/債権法改正と実務上の課題」第1回「法定利率」(本ジュリスト60頁以下)に気になった記述があったので、ざっくり検討してみました。
1. 気になった記述—法定利率と市場金利の逆転・マイナス法定利率
本ジュリストの「法定利率」は、能見善久教授と中井康之弁護士が、債権法改正後の法定利率について、対談形式で深く検討するといった内容の記事なのですが、その中で、能見教授が以下のご発言をされていました。
「それは、1%以下の変動率は考慮しないということからくるのですが、現在は法定利率のほうが市場利率よりも高いところにありますが、それが逆転するという状態が生じるのではないかということです。」(本ジュリスト64頁左側)
「仮に、市場金利が法定利率を超えることがありうるとすると、そこから市場金利が下がる場面で、法定利率がマイナスになることもありうるかと思ったのですが、私の404条の読み方が正しくないかもしれないので、これ以上は深入りするのはやめます。」(同頁右側)
正直、とても興味深いです。ここは、能見教授に代わって無謀にも深入りし、どなたか知見のある方からのご指摘を待ちたいと思います。
2. 債権法改正後の法定利率(改正民法404条)
ざっと確認しましょう。内容をご存知の方は読み飛ばしていただいて結構です。まず、条文を引用します。
(法定利率)
第四百四条 利息を生ずべき債権について別段の意思表示がないときは、その利率は、その利息が生じた最初の時点における法定利率による。
2 法定利率は、年三パーセントとする。
3 前項の規定にかかわらず、法定利率は、法務省令で定めるところにより、三年を一期とし、一期ごとに、次項の規定により変動するものとする。
4 各期における法定利率は、この項の規定により法定利率に変動があった期のうち直近のもの(以下この項において「直近変動期」という。)における基準割合と当期における基準割合との差に相当する割合(その割合に一パーセント未満の端数があるときは、これを切り捨てる。)を直近変動期における法定利率に加算し、又は減算した割合とする。
5 前項に規定する「基準割合」とは、法務省令で定めるところにより、各期の初日の属する年の六年前の年の一月から前々年の十二月までの各月における短期貸付けの平均利率(当該各月において銀行が新たに行った貸付け(貸付期間が一年未満のものに限る。)に係る利率の平均をいう。)の合計を六十で除して計算した割合(その割合に〇・一パーセント未満の端数があるときは、これを切り捨てる。)として法務大臣が告示するものをいう。
これ、何を言っているのか、分かりにくいですよね(特に4項と5項)。潮見佳男『民法(債権関係)改正法の概要』57頁を引用します。
①最初は3%の法定利率からスタートしたうえで、②3年ごとに法定利率の見直しを行う。③その際、過去5年間の平均利率をもとに導かれた「基準割合」と直近変動期(中略)の「基準割合」の差をとり、④この差が1%を超えたときには、(小数点以下を切り捨てたうえで)この差を「直近変動期の法定利率」に加算または減算する処理を行う。
うーん、なるほど。まだ、ちょっとよく分からない。説明を加えます。
まず、上記②の「3年ごと」ですが、これは、改正民法の施行年である2020年をスタート年として、2020年から2022年までが第1期、2023年から2025年までが第2期、といった具合になります。「3年ごと」の期間を「期」と呼びます。
次に、上記③の「過去5年間」ですが、これは、各期の最初の日が属する年の6年前の年をスタート年とした5年間です。たとえば、第1期の最初の日は2020年1月1日か同年4月1日(この点については、下記5ご参照)なので、その日が属する2020年の6年前の2014年をスタート年とした5年間(つまり、2014年1月1日から2018年12月31日まで)となります。
また、上記③の「平均利率」は、短期貸付け(貸付期間1年未満の貸付け)の平均利率(各月に行った短期貸付けの利率の当該月における平均)のことです。より具体的には、「日本銀行が毎月発表する、国内銀行の『貸出約定平均金利(新規・短期)』(国内銀行の当該月末貸出残高のうち、当月中において実行した貸出で、約定時の貸出期間が1年未満の貸出に関する利率の平均)」との理解です(民法(債権関係)部会資料74B「民法(債権関係)の改正に関する要綱案の取りまとめに向けた検討(10)」
(http://www.moj.go.jp/content/000120402.pdf)4頁)。法定利率と市場金利(市中金利)の文脈においては、この「平均利率」が市場金利を意味します。
続いて、上記③の「基準割合」ですが、これは「過去5年間」における各月の「平均利率」の平均値のことです。以下、その計算方法を説明しますが、「基準割合」は「ある期が始まる1年程度前までには告示されることが予定されている」ため、実際には、自分で計算する必要はありません(筒井=村松『一問一答 民法(債権関係)改正』84頁(注2))。では、「基準割合」の計算方法ですが、たとえば、第1期の「過去5年間」である2014年1月1日から2018年12月31日までの期間における各月の「平均利率」につき、最初2年間が全て1%で、残り3年間が全て0.5%だった場合、以下の計算により、当該期間の「基準割合」は0.7%になります。
(1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+0.5+0.5+0.5+0.5+0.5+0.5+0.5+0.5+0.5+0.5+0.5+0.5+0.5+0.5+0.5+0.5+0.5+0.5+0.5+0.5+0.5+0.5+0.5+0.5+0.5+0.5+0.5+0.5+0.5+0.5+0.5+0.5+0.5+0.5+0.5+0.5)÷60=0.7
要は、「過去5年間」の各月の「平均利率」を合算して(1か月の「平均利率」1%×12か月×2年+1か月の「平均利率」0.5%×12か月×3年)、それを60か月(5年)で割れば、「基準割合」が算出できます。仮に、上記のように、各年の月ごとの「平均利率」が当該年において全て同じ値という場合には、よりシンプルに、各年の「平均利率」の合計値を5で割ることで、「基準割合」を算出できます。
(1+1+0.5+0.5+0.5) ÷5=0.7
ここまで来れば、もう一息です。現時点の期(当期)の「基準割合」と「直近変動期」の「基準割合」をそれぞれ算出し、その差を見ます。ここで、「直近変動期」とは、法定利率に変動のあった期のうち当期から最も近い過去の期のことをいいます。それまで変動がなかった場合は、第1期の「基準割合」との差を見ていくことになります(附則第15条第2項)。たとえば、第2期(当期)の「基準割合」が1.5%、第1期の「基準割合」が0.3%の場合、その差は1.2%なので、その小数点以下を切り捨てた1%が第1期の法定利率であった3%に加算され、その結果、第2期(当期)の法定利率は4%となります。
以上を図にまとめると、以下のようになります。この図では、「平均利率」は2016年までは0%、2017年以降は毎年0.5%ずつ上昇していくが、各年の月ごとの「平均利率」は同じ値(たとえば、2017年は1月から12月まで常に0.5%)という設定にしています(この設定は『Before/After 民法改正』98頁の問題と同じです。)。
【図1−1】

(1) 第2期(当期)の「基準割合」は、(0.5+1+1.5+2+2.5)÷5で、1.5%(「基準割合」の行のブルー部分)
(2) 第1期の「基準割合」は、(0+0+0+0.5+1)÷5で、0.3%(「基準割合」の行のイエロー部分)
(3) 各「基準割合」の差は、1.5−0.3で、1.2%(「差」の行の赤枠部分)
(4) 第2期の法定利率は、上記1.2%から小数点以下を切り捨てた1%を、第1期の法定利率である3%に加算して、4%
これをグラフにすると、以下のようになります。
【図1−2】

3. 検証その1—法定利率と市場金利の逆転
分かりやすく、先ほどと同じ以下の設定で試算してみましょう。
「平均利率」は2016年までは0%、2017年以降は毎年0.5%ずつ上昇していくが、各年の月ごとの「平均利率」は同じ値(たとえば、2017年は1月から12月まで常に0.5%)とする。
以下が試算結果です。
【図2】


おー、たしかに逆転しますね。まあ、これは、「基準割合」の差のうち小数点以下を切り捨てる(法定利率に反映させない)との取扱いから、想像に難くない結果であろうかと思います。
ところで、このような逆転現象は現実に起こり得るのでしょうか。そう簡単には起こらないように思いますが、「平均利率」が短期間で急上昇した場合には、それが法定利率に反映されるまで一定のタイムラグがあるため、一時的な逆転が生じることになろうかと思います。一応、図で示しておきます。
【図3】


4. 検証その2—マイナス法定利率
これが非常に気になっていました。日銀のマイナス金利政策の対応に苦労させられた経験がありますが、法定利率がマイナスになったら、それどころの騒ぎでは済まないので。
では、以下の設定で試算してみましょう。
前半の「平均利率」は各期の「基準割合」の差が1.9%となるように調整する。後半の「平均利率」は各期の「基準割合」の差がマイナス1%又は2%となるように調整する。
上記により、前半は、「平均利率」はどんどん上昇しているのに、0.9%を切り捨ててしまうが故に、法定利率は(3年ごとに1%ずつ緩やかに上昇するものの)「平均利率」の上昇に付いていけず、他方で、後半の「平均利率」の減少については、各期の「基準割合」の差に小数点以下の端数が出ないため、法定利率は当該減少の影響を100%受けることになります。
さて、お待ちかねの結果ですが、以下のようになりました。
【図4】

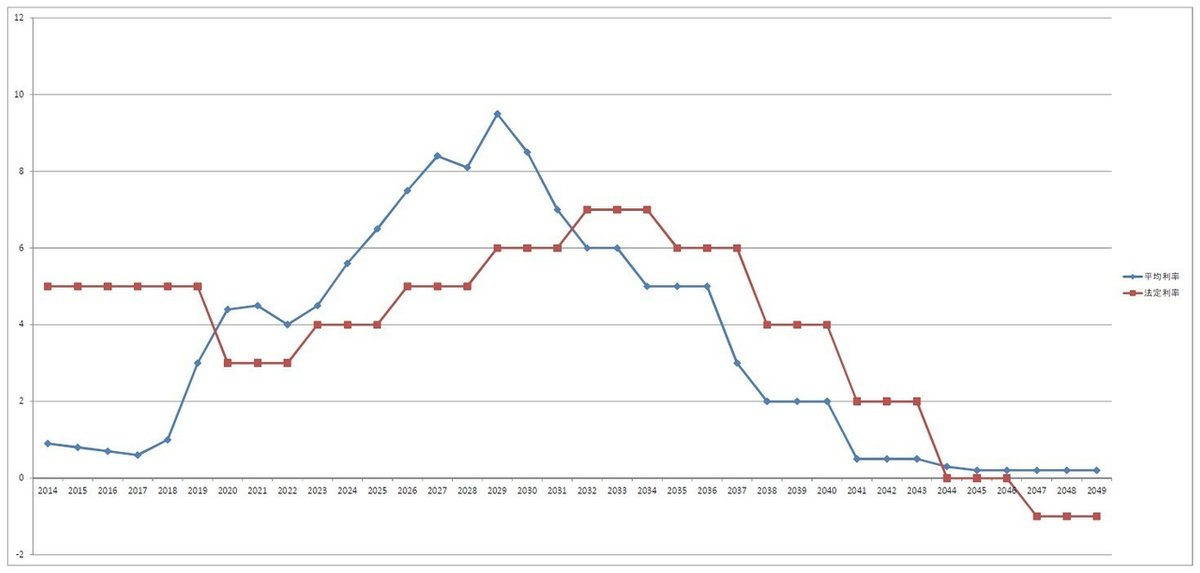
無事(?)、法定利率がマイナスになりました。能見教授の慧眼すごい。
とはいえ、現実には、マイナス法定利率に陥る事態は、起こり難いように思われます。色々と「平均利率」を変えて検証してみましたが、急上昇した後に急下降するように組んでも、よほど極端な値を設定しない限り、0%にはなっても(それはそれで問題ですが)、マイナスまで行くケースはありませんでした。
5. おまけ—各期の最初の日は1月1日か4月1日か
改正民法の施行日が2020年4月1日であることからすると、2020年4月1日が第1期の最初の日となり、その結果、第1期の最後の日は2023年3月31日となるようにも思われます。
しかし、これだとなんだか分かりにくい。「基準割合」に係る「過去5年間」が1月1日を最初の日としていることもあって、余計分かりにくい。
実はこれ、まだ決まっていないのです。民法(債権関係)部会資料81B「民法(債権関係)の改正に関する要綱案の取りまとめに向けた検討(17)」
(http://www.moj.go.jp/content/000125160.pdf)6頁に、以下のように書かれています。
「なお、この3年を一期とする仕組みが具体的にいつの時点から開始するか(1月1日か、4月1日かなど)については、技術的・細目的事項であることから、法務省令に委任することとする。」
なお、この点につき、前掲『一問一答 民法(債権関係)改正』84頁(注1)には、「改正法は平成32年4月1日から施行されるため、4月1日が初日となるものと考えられる」とありますが、これはどうでしょうか。上記のとおり、そのほうが素直ではありますが、論理必然ではないように思います。個人的には、今のところ、分かりやすさの観点から、1月1日を初日にしてほしいと思ってはいますが、果たしてどうなるか。法務省令案の発表を待ちたいと思います。
