機械学習を使って日本の電力需要を予測してみました
2022年に入ってからインフレの影響で身近な物やサービスの物価が上昇しているのはみなさんも肌で感じていると思います。個人的に一番気になっているのは電力やガスといったユーティリティの料金が一年前と比べて圧倒的に高くなったことです。ユーティリティのインフレは政治的な問題も含めて幾つか要因はあるかと思いますが、国内の電力需要はインフレによってどう変わるのかが気になったため、教師あり学習で検証してみました。
実行環境
Python3
Windows 11
Chrome
Google Colaboratory
分析のフロー
電力需要予測の分析を行うためのフローは以下の通りです。
①電力需要データを取得する
②データの前処理を行う
③需要データの中身を分析してみる
④学習データとテストデータに分割する
⑤モデルを構築する
⑥SARIMAモデルによる予測
それでは、それぞれのフローの詳細を説明していきます。
①電力需要データを取得する
まずは東京電力が公開している電力需要のページからcsvファイルを取得します。ただし、先頭の2行が邪魔になるため、後半のコードでは先頭2行を削除しています。
コード
import pandas as pd
import numpy as np
import warnings
import itertools
import statsmodels.api as sm
import matplotlib.pyplot as plt
from statsmodels.tsa import stattools as st
from plotly import tools
from plotly.graph_objs import Scatter, Figure, Layout
from plotly.offline import iplot
col_names = ['DATE','TIME','実績(万kW)']
years = [2019, 2020, 2021, 2022];
for i in years:
df = pd.read_csv("https://www.tepco.co.jp/forecast/html/images/juyo-"+ str(i) + ".csv",names = col_names,encoding = 'shift_jis')
print(df.head())
df = df.drop(index=[0, 1])
df.index = np.arange(1, len(df)+1)
df.to_csv("dataset.csv")
with open("/content/dataset.csv", "r") as csvfile:
print(csvfile.read())出力

東京電力が公開している2022年のデータ1年分を読み取り、1時間ごとのデータとして取得できました。今回はcolaboratoryの処理性能の問題で、2022年の一年分のみを取得しています。
②データの前処理を行う
取得したままのデータでは日付のデータが文字型になっていたりするため、そのままでは需要予測ができません。そこで、前処理を行います。
コード
#DATE列とTIME列を結合し、日付・時間の情報をDATETIME列に格納
df['DATETIME'] = df['DATE'].str.cat(df['TIME'].astype(str), sep=' ')
df.describe
#DATE、DATETIME列をdatetime型に変換
df["DATE"] = pd.to_datetime(df["DATE"])
df["DATETIME"] = pd.to_datetime(df["DATETIME"])
#インデックスにDATETIMEを設定しそれ以外を削除
df_ds = df.drop(['DATE','TIME'], axis=1)
df_ds.index=df_ds["DATETIME"]
del df_ds["DATETIME"]
df_ds=df_ds.astype('float64')
df_ds
df_ds.plot()出力

表のままではイメージしづらいのでプロットしてみるとこのようなグラフになります。

③需要データの中身を分析してみる
プロット結果からも電力需要には季節ごとの変化があるように見えます。そこで、時系列データの自己相関と成分分解を実施することでデータを分析してみます。
コード③-1 自己相関
# 自己相関(ACF)のグラフ作成
fig, (ax1, ax2) = plt.subplots(nrows=2, sharex=True)
sm.graphics.tsa.plot_acf(df_ds['実績(万kW)'], lags=40, ax=ax1)
sm.graphics.tsa.plot_pacf(df_ds['実績(万kW)'], lags=40, ax=ax2)出力

コード③-2 成分分解
#成分分解
res = sm.tsa.seasonal_decompose(df_ds['実績(万kW)'], period=24)
# res.plot()
fig = tools.make_subplots(rows=4, cols=1)
fig.append_trace(Scatter(x=res.observed.index, y=res.observed, name='Original'), 1, 1)
fig.append_trace(Scatter(x=res.trend.index, y=res.trend, name='Trend'), 2, 1)
fig.append_trace(Scatter(x=res.seasonal.index, y=res.seasonal, name='Seasonal'), 3, 1)
fig.append_trace(Scatter(x=res.resid.index, y=res.resid, name='Resid'), 4, 1)
fig['layout'].update(title='成分分解')
iplot(fig)出力

コード③-3 定常性に関する分析
時系列解析を行う上では季節性などの一定の規則性がないかを調べることが重要です。そこで定常性の有無を調べてみました。
#定常性を持つかを判断(結果が0.05未満で定常性あり)
res = sm.tsa.stattools.adfuller(df_ds['実績(万kW)'])
print('p-value = {:.4}'.format(res[1]))出力
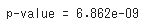
これらの結果からも電力需要が定常性を持っていることが分かりました。
④学習データとテストデータに分割する
コード
traindata = df_ds[df_ds.index < '2022-11-01 00:00:00']
testdata = df_ds[df_ds.index >= '2022-11-01 00:00:00']ここでは、1月から10月までのデータを学習データ、11月と12月の2ヵ月分をテストデータという分け方にしています。
⑤モデルを構築する
時系列分析でよく用いられるモデルは幾つか代表例がありますが、今回はSARIMAモデルという代表的なモデルを使用します。
SARIMAモデル(Seasonal AutoRegressive Integrated Moving Average)は、代表的な時系列解析用のモデルであるARIMAモデル(自己回帰和分移動平均:autoregressive integrated moving average)に「季節的な周期パターン」を加えたモデルです。つまり、季節性があるデータに対してARIMAモデルよりも柔軟に対応できるのがSARIMAモデルです。
そもそも、ARIMAモデルとは以下の3つの成分から成り立っています。
AR (Auto-Regressive) component:自己回帰成分
I (Integrated) component:和分成分
MA (Moving Average) component:移動平均成分
簡単な説明になりますが、ARとは自己相関(過去の値に依存すること)、Iとは和分(過去との差分によって階差系列を作り値を定常化する前処理を行うこと)、MAとは移動平均(ARだけで自己相関をモデル化できないため、残差の移動平均をとることでモデル化を実現すること)という意味です。
これらの成分によって、上昇下落のトレンドを解析することができるようになります。
参考文献1:https://bigdata-tools.com/arima-sarima-model/
参考文献2:https://www.salesanalytics.co.jp/datascience/datascience087/
コード
from statsmodels.tsa.statespace.sarimax import SARIMAX
# SARIMAモデルを適当な数値で推定する
SARIMA = sm.tsa.SARIMAX(traindata, order=(4,1,2),
seasonal_order=(1,1,1,24),
enforce_stationarity=False,
enforce_invertibility=False).fit()
print(SARIMA.summary())SARIMAモデルのパラメータについて
SARIMAモデルには引数となるパラメータを設定する必要があります。基本的には、SARIMAX(データ,order=(p,d,q),seasonal_order=(sp,sd,sq,s))という引数を指定します。
最初の3つのパラメータp,d,qは、ARIMAに適用するAR,差分,MAの次数を指定します。
sp,sd,sqはそれぞれ「季節性自己相関」「季節性導出」「季節性移動平均」をsは季節周期を指定します。12カ月周期ならs=12となります。
参考文献:https://qiita.com/ngayope330/items/8d8aac6db1f88e8abe25
出力

⑥SARIMAモデルによる予測
コード SARIMAモデルによる予測
# 予測
train_pred = SARIMA.predict()
test_pred = SARIMA.forecast(len(testdata))
test_pred_ci = SARIMA.get_forecast(len(testdata)).conf_int()
print(test_pred_ci)
#RMSEを用いた精度計測
from sklearn.metrics import mean_squared_error
import numpy as np
train_rmse = np.sqrt(mean_squared_error(traindata, train_pred))
test_rmse = np.sqrt(mean_squared_error(testdata, test_pred))
print('RMSE(train): {:.5}\nRMSE(test): {:.5}'.format(train_rmse, test_rmse))出力

SARIMAモデルで予測した学習データとテストデータの結果について、RMSEを用いてそれぞれ評価しました。
RMSE(Root Mean Squared Error)はその値が小さければ小さいほど、誤差の小さいモデルであると言えます。
テスト用のデータの結果からもこのモデルではイマイチの精度かもしれませんが、一旦プロットしてみます。
コード SARIMAモデル予測結果のグラフプロット
df_merge = pd.merge(testdata,test_pred,left_index=True, right_index=True, how ="outer", indicator=True)
df_merge.plot()出力

Prophet を使った時系列データ予測
ここまでせっかく作成してきたんですが、チューニング不足のせいか学習用のデータ不足が原因なのか、現状ではSARIMAモデルだとRMSEの精度が低いことから、SARIMAモデル以外の仕組みを用いて予測してみたいと考えました。
そこで用いたのがProphetというライブラリです。
Prophetは時系列データ分析で用いられるライブラリの中でも非常に使いやすいのが特徴です。
Prophetは、2017年にFaceBook社が開発した時系列解析用のライブラリで、近年、売上金額や来客数などの時系列解析の定番ライブラリとなっています。
このProphetでは、次のような式を使います。
y=g(t)+s(t)+h(t)+ϵ_t
y(t):予測する変数
g(t) :トレンドの項
s(t) :周期性の項
h(t) :祝日効果(イベント効果)の項
ϵ_t :正規分布に従う誤差項(ノイズ)
Prophetの優れた点には次のような特徴があります。
予測結果を解釈しやすい
難しい統計学の知識がなくてもモデル作成可能
上記の特徴から、使いやすいことがお分かりになるかと思います。ということで、代替案としてこのProphetを使ってみました。
参考文献1:https://blog.kikagaku.co.jp/plotly
参考文献2:https://www.skillupai.com/blog/tech/prophet/
参考文献3:https://qiita.com/japanesebonobo/items/26cccef8ee9d45006093
コード Prophetを用いた予測
# ライブラリの install
!pip install pystan==2.19.1.1
!pip install fbprophet
!pip install plotly
# ライブラリのインポート
from fbprophet import Prophet # ライブラリの読み込み
from fbprophet.plot import plot_plotly
import plotly.offline as py
pf_train = traindata.reset_index().rename(columns={'DATETIME': 'ds', '実績(万kW)': 'y'})
pf_test= testdata.reset_index().rename(columns={'DATETIME': 'ds', '実績(万kW)': 'y'})
# インスタンス化
#changepoint_prior_scaleという引数を使うことで過学習や学習しきれない場合に対してスパースの優先度の大きさを調整できます。
pmodel = Prophet(changepoint_prior_scale=0.8)
# 学習
pmodel.fit(pf_train)
# 学習データに基づいて未来を予測
# future = pmodel.make_future_dataframe(periods=72,freq="H")
forecast = pmodel.predict(pf_test.loc[:72, ["ds"]])
forecast出力

コード 予測結果の可視化
x=pf_test.ds[:72]
y=pf_test.y[:72]
plt.plot(x,y, label='Original', linestyle="dashed")
plt.plot(forecast.ds,forecast.yhat)
plt.show()出力

需要予測結果がオレンジの実線、実際の需要が青色破線です。需要量が小さい時の精度がイマイチですが、需要が多い時の予測はまずまずと言えそうです。
まとめ
SARIMAモデル、Prophetそれぞれを用いた予測では、ある程度の精度で電力需要予測ができることが分かりました。
今回の分析に用いたデータは1年分でしたが、対象の年数を増やしてより長期間のデータを用いるか、学習回数を増やすことでより精度が上がる結果になるんじゃないかと思います。チューニングによってパラメータをより適切な内容に変えることも改善策として考えられます。
初めて機械学習の予測モデルを自分で作りましたが、アウトプットとして形にできたのは良い経験になったとおもいます。
