[2.91]Blenderで正多面体を

サイコロ作りたい場合はこちらの早口ビデオを見てもらうとして、Blenderでちょっとした遊びをしてみませんか？

「正多面体をいくつかBlenderで作ってみよう」というヤツです。

日本数学会の会員誌「数月通信」14巻1号にあるような感じの内容に少しだけリンクします。

日本数学会--会員誌「数学通信」--第１４巻第１号目次

・ 「正多面体の中に正多面体：複合正多面体」(PDF)

では始めていきましょう。

正6面体

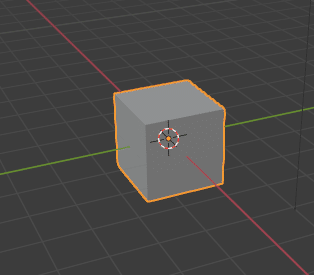
Blender起動したらそこにある箱、立方体です。最初からあるのでこれは一先ずクリア、ということで良いですか？

正20面体

基本図形として用意されている Ico Sphere のSubdivisions=1 がそれです。オブジェクトモードで [Shift]+[A]の追加メニューから、 Add Mesh>Ico Sphere をクリックしてオブジェクトを追加します。直後に、パラメータの一つ、Subdivisions の値を1 にします(デフォルトは2)

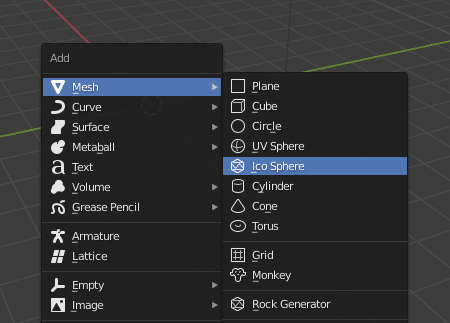
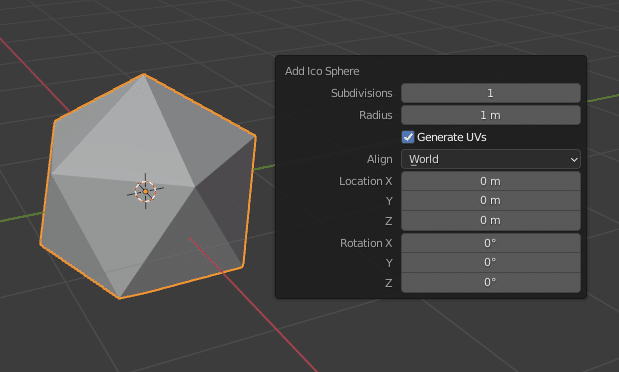
Add Meshコマンドでオブジェクトを追加した直後に左下のパネル、または[F9]キーを押して出てくるパネルからSubdivisions の値を変更しましょう。

正12面体

上記の正20面体から作ります。途中まではサッカーボールの作り方に似てたりします。

オブジェクトモードで [Shift]+[A]の追加メニューから、 Add Mesh>Ico Sphere をクリックしてオブジェクトを追加します。直後に、パラメータの一つ、Subdivisions の値を1 にします。

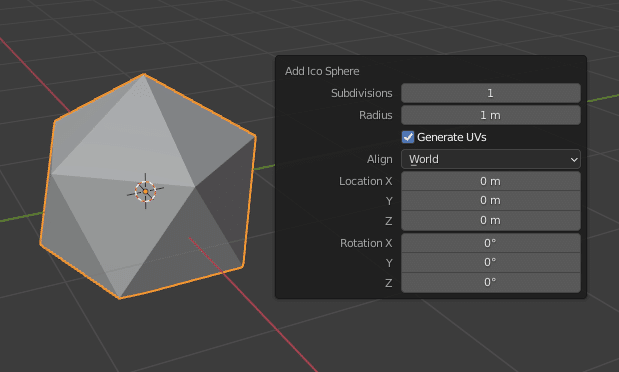
次に[TAB]キーでエディットモードに入ります。

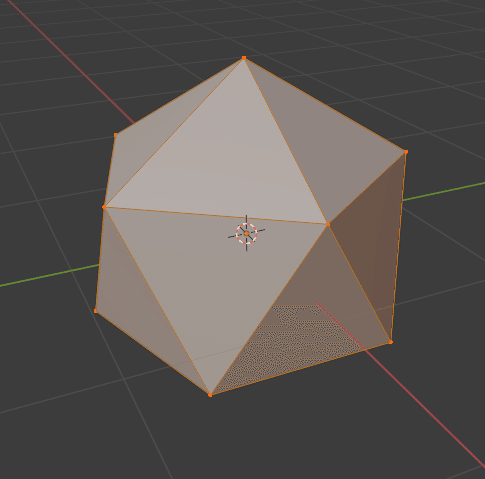
全ての頂点が選択された状態で、

[F9]キーを押して Number of Cuts の値を 2 にします。

尖っている部分の頂点を一つ選択します。

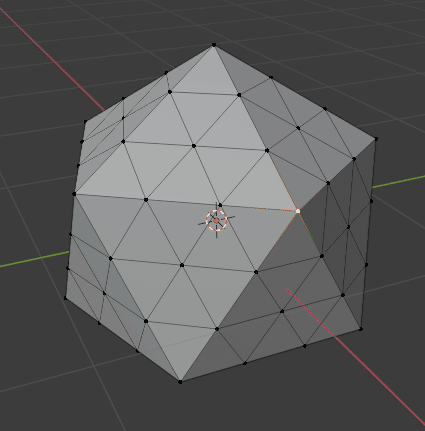
共通する要素を選択するために、[Shift]+[G] を押して、メニューから Amount of Connecting Edges を選択して頂点に接続されている辺の数が同じものを選択します。

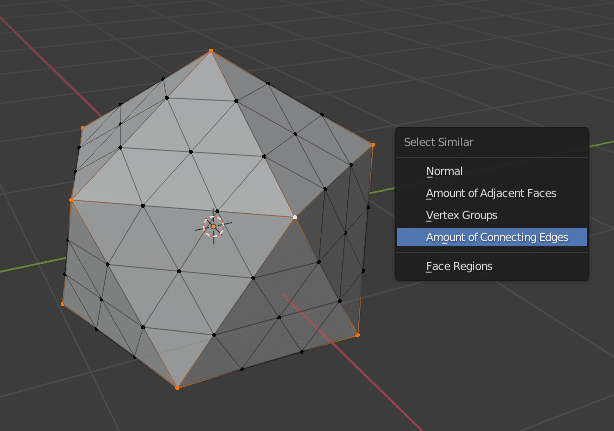
その状態で Select > Select More/Less > More ([Ctrl]+[Num+])で選択頂点を拡げます。

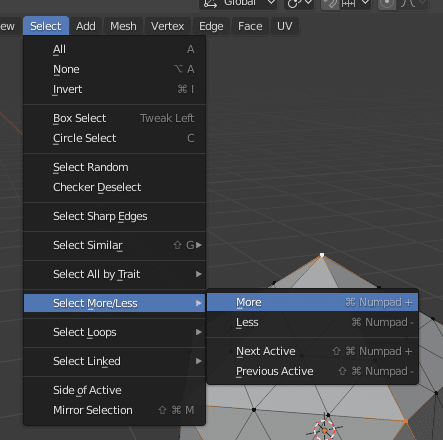
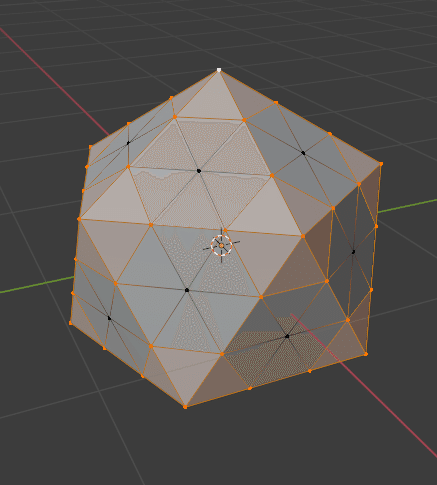
この選択状態のまま [X]の削除メニューから Dissolve Edges をクリック。

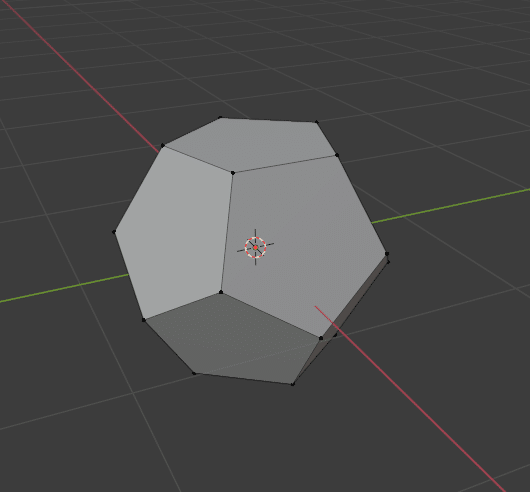
正12面体から正6面体

正12面体を構成する5角形を以下のようなパターンになるように、3角形+四角形に分割する辺を作成します。正面から見たら正方形が出来ているように。

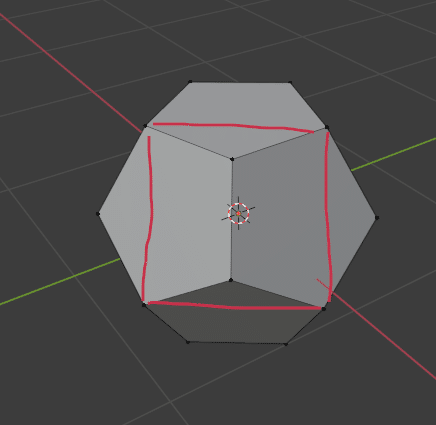
2点を選択して Vertex Connect コマンド([J]) で辺を作っていきます。

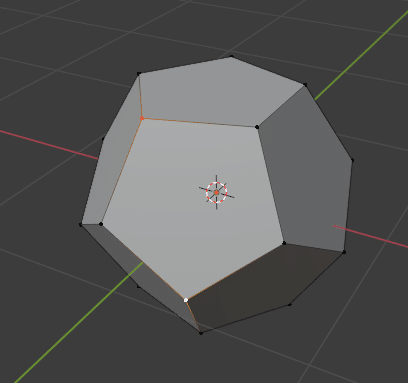
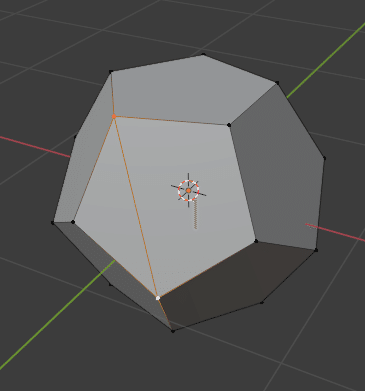
視点をグルグル回転させながら繰り返していきます。

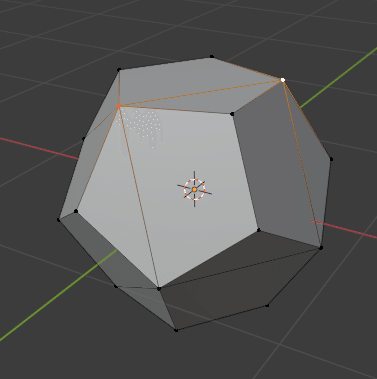
最後にVertex Connect を実行した状態で、[2]キーを押して辺選択モードにしてから、 [Shift]+[G] を押してメニューから Length を選択します。

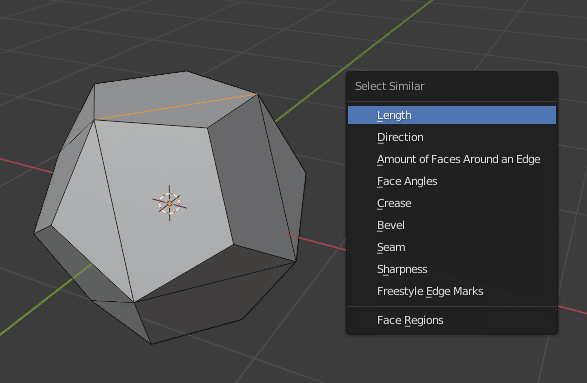
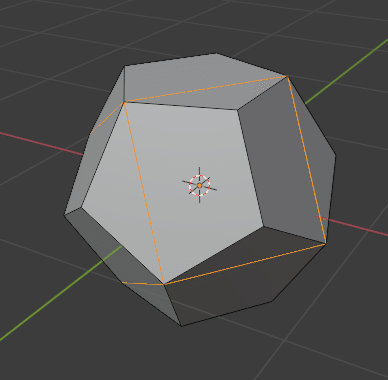
この状態で[1] キーを押して頂点選択モードにします。そこから[Ctrl]+[I]で選択状態の反転、[X] の削除メニューから Dissolve Vertices で頂点を溶解させます。

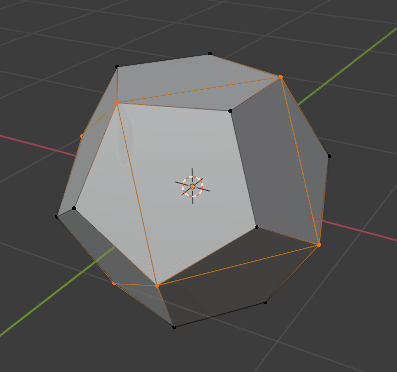
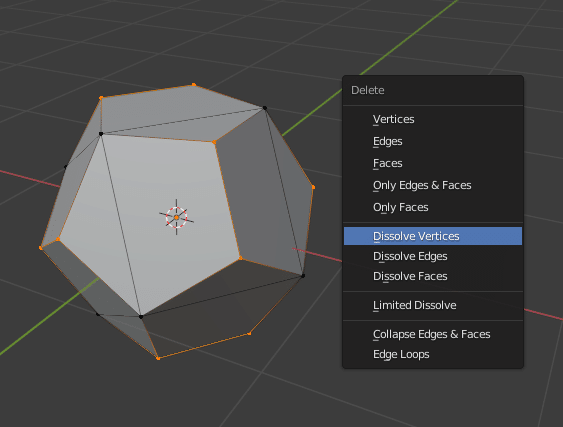
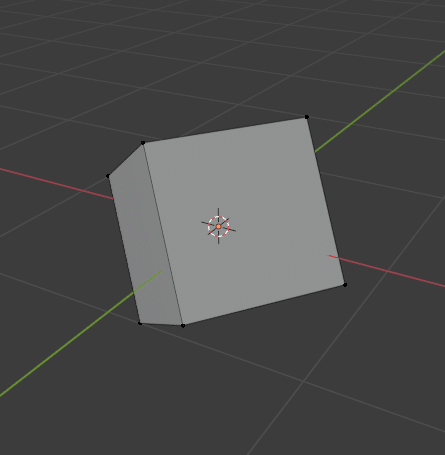
正6面体から正4面体

だいたい前段から察している方もいると思います。

正面から見て3角形になるように辺を追加して、3角形の中心に相当する頂点を選択、溶解させればOKですね。

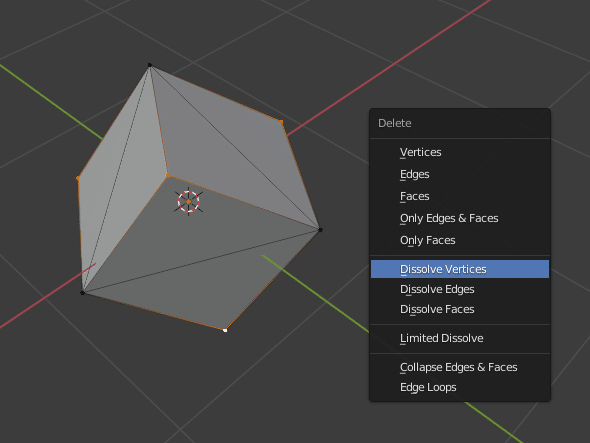
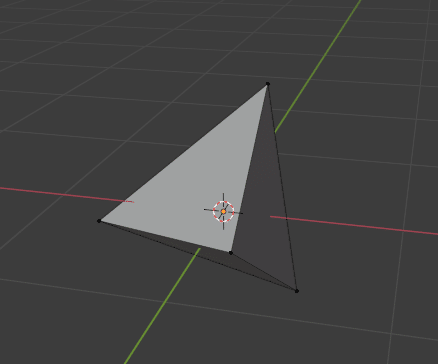
4/5を制したことになります

正多面体は5種類しかないので、上記で4/5はBlenderで作れることがわかりました。「我はBlenderで世界の八割の真理を得た！」とかまあそういうことですね。

メッシュオブジェクトにおいて、 頂点/辺/面 について同じコマンドでも結果が異なったりすることを覚えておくことで効率的な編集が可能になることもある、というくらいで覚えておいてもらったらいいのかな、と思います。

・ Select similar - [Shift]+[G]
・ Delete - [X]
・ Vertex Connect - [J]

[追記]辺の長さを知りたい

こういう感じで表示されるようにするには、エディットモードで全ての頂点を選択して、丸が2つ重なっているアイコン()の横[v]をクリックすると出てくるViewport Options パネルから、Measurements > Edge Length にチェックを入れてみてください。

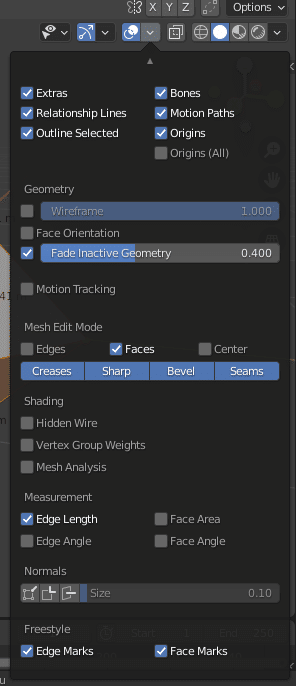
See Also: