[聴覚心理]院試備忘録1.音の物理基礎

1-1.キーワード

音圧,音圧レベル,音の強さ,フェヒナーの法則,ERB尺度,メル,フーリエ変換,スペクトル,フィルタ,周波数特性

1-2.物理現象としての音

音波とは波動現象です。
波動現象とは振動が媒質に伝わっていく現象です。
音波においては空気という媒質に、空気の粒子の振動が伝わっています。
また、音波は縦波(疎密波)であり、つまり粒子が密の部分と疎の部分がある波です。
この疎と密はすなわち大気圧より圧力が高い、低いということを意味しています。
この大気圧からのズレを音圧と言います。

1-3.音の強さと大きさの導入

強さと大きさは異なります。
強さは物理量であるのに対し、大きさは心理量です。
まずはインテンシティ,ラウドネス,音圧レベル,音圧,音響パワーレベルという量があります。
これらの関係性と意味を俯瞰できるようになりましょう。
単位として次のようなものが知られています。
[phon], [sone], [dBSPL], [dBHL], [Pa], [W/m^2]...
最初に最小可聴音圧P0=2.0*10^-5[Pa]を導入します。
話し声の音圧を測定してみるとP=2.0*10^-2[Pa]と測定できたとします
音圧P=2.0*10^-2[Pa]
→音圧の比P/P0=10^3[単位無し]
→強さの比(P/P0)^2=10^6[単位無し]
→音圧レベル10*log(10,(P/P0)^2)=60[dBSPL]
1)音圧レベル10*log(10,(P/P0)^2)=60[dBSPL]:物理量
→声が175[Hz]だとすればラウドネスレベル=40[phon]:心理量
→ラウドネス=1[sone]:心理量
次に関しては聴覚という点においてはあまりきにする必要はないのかなとは思いますが一応
2)音響インテンシティは音の強さの物理量です
定義は「単位時間に単位面積を通過する音のエネルギー量」です
音響インテンシティI=(P^2)/ρc[W/m^2]
音の強さのレベルL=10*log(10,I/10^(-12))[dB]
デシベルのデシとは10という意味です。
デシリットルのデシ、ディケイドのdec、10角形(decagon)のdecなどは全て10という意味です。

1-4.波の表現としての音

あらゆる音は波形として表現できます。
そしてあらゆる波形は三角関数の足し合わせとして表すことができます。
これをフーリエの定理といい、足し合わせとして表現する際の演算をフーリエ級数展開やフーリエ変換といいます。
この操作によってどの周波数がどのくらいの強さで混ざっているかという表現をすることができます。
この周波数と強さ(振幅)の関係をスペクトルといいます。
下の二つを見比べると、高周波数部分で差異が見られます。
子音の"s"は「さ」から「あ」を引くことで確認できます。(雑な処理ですいません)
例)「あ」という音のスペクトル

例)「さ」という音のスペクトル

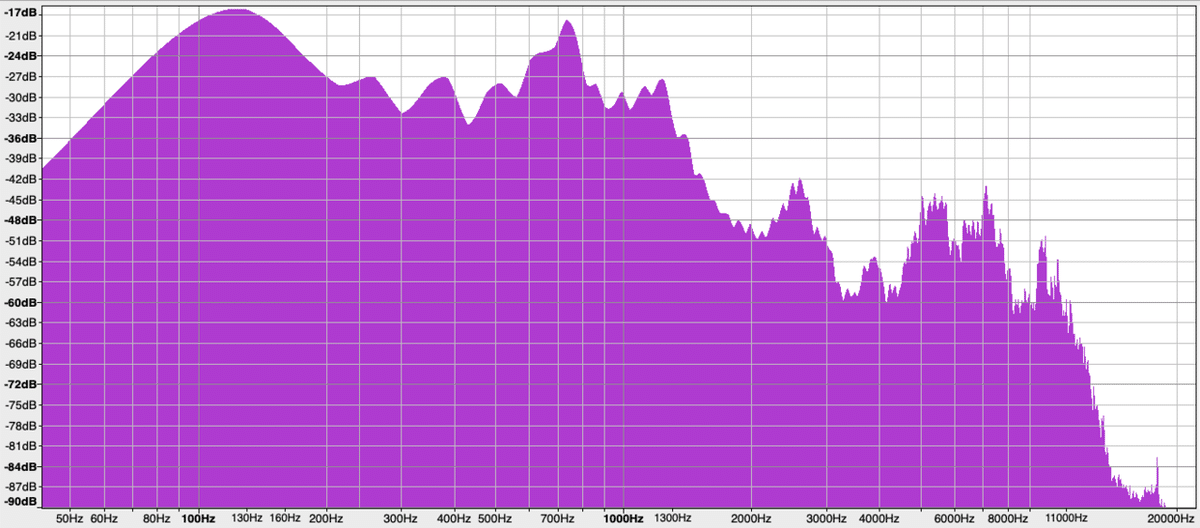
例)"s"という音のスペクトル

1-5.フィルタという概念

外耳や中耳、内耳ではその形状や細胞の振る舞いから、入出力の信号のスペクトルが変化します。
この変化をフィルタといいます。
実際にどうなるのか試してみましょう
例)「あ」という声をフィルタリング

1.「あ」のスペクトル(再掲)

2.掛け合わせるローパスフィルタ(500Hzから6dB/oct減衰)

3.掛け合わせた結果

フィルタという考え方を端的にいうなら「入力に対して何らかの出力をするシステム」と言えるのではないのでしょうか。
後に出てくる内耳ではBPF(バンドパスフィルタ)というものをイメージしていただくと理解がしやすいです。
BPFとはある周波数帯域のみを通して、他の周波数をカットするフィルタです。

1-6.まとめ

今回は音とは何か、音をどのように表現するかをかなり駆け足でみてきました。
音を表現するとき、周波数と強さで表現するのに必要な計算がフーリエ変換です。
スペクトルとフィルタ、音圧パワーレベルがわかっていれば聴覚の話はほとんどわかると思います。
スペクトルはどの周波数がどのバランスで混ざっているか、フィルタは周波数と振幅の関数で表すことができるシステムでしょう。

1-7.furthermore

等ラウドネス曲線
ERB尺度,Bark尺度,mel尺度
フーリエ変換,フーリエ級数展開
高速フーリエ変換(FFT)
濾波(フィルタリング)と変調
周波数特性
ホワイトノイズ、ピンクノイズ