
工業系を学ぶ者が知っていて損はないプラネタリギヤについて学ぼう
歯車(ギヤ)とは
歯車(はぐるま)とは、機械要素の一つで、回転運動を伝えるために歯が刻まれた部品です。一般的には「ギヤ」と呼ばれています。2つ以上の歯車を組み合わせて使用し、動力を伝達したり、回転速度やトルク(回転力)を変化させたりする役割を果たします。
歯車には平歯車、はすば歯車、かさ歯車、ウォームギヤ、ラックとピニオンなどがあり一見して作動は理解し易いです。しかし、プラネタリギヤはいくつかの歯車が組み合わさっておりその作動はやや複雑です。
プラネタリギヤとは
図に示すように、インターナル・ギヤ、プラネタリ・キャリヤ、サン・ギヤ、プラネット・ギヤから構成されています。

特徴と利点:
小型で高出力:複数の遊星歯車で動力を分散するため、小型ながら大きなトルクを伝達できます。
同軸入力・出力:入力軸と出力軸を同軸上に配置できるため、機械の設計が容易になります。
変速比の変更が容易:構成要素の固定・入力方法を変えることで、様々な変速比を実現できます。
効率が良い:動力伝達効率が高く、エネルギーロスが少ないです。
用途:
自動車のオートマチックトランスミッション: 変速機構として広く使用されています。
ハイブリッド車、電気自動車: モーターとエンジンの動力分配、変速に利用されています。
建設機械: 大きなトルクが必要なクレーンやショベルカーなどに使用されています。
航空機: エンジンの減速機などに使用されています。
産業用ロボット: 関節の駆動などに使用されています。
それぞれのギヤまたはキャリヤを固定したり回転させたりすることにより変速比や回転方向を変えることができます。
プラネタリギヤの変速比
しかし、何を固定して、何を入力にすれば変速比はいくらになり回転方向はどちらかと考えると下の表のようになり大変複雑になります。

ましてや、自動車のオートマチック・トランスミッションのようにプラネタリギヤを2段に連結させたりするとどのように考えればよいかわからなくなってしまいます。
そこで役に立つのが速度線図です。
速度線図を用いると一目で回転速度、回転方向が求められます。
描き方は以下のようになります。
速度線図の作画
3本の縦線を描きます。
必ず、キャリヤの線が真ん中になります。
インターナルギヤとサンギヤは左右どちらでも構いません。
キャリヤとインターナルギヤの間隔とキャリヤとサンギヤの間隔を図のように歯車の歯数比にします。比ですので比を保っていれば基準になる間隔はいくらでも構いません。

速度線図の使い方
例として、サンギヤとインターナルギヤの歯数比が1:2のプラネタリギヤを考えてみましょう。
問題 キャリヤの回転数を求める ???$${min^{-1}}$$
条件:
インターナルギヤ 回転速度$${0min^{-1}}$$(固定)
サンギヤ 回転速度$${1200min^{-1}}$$
下図のようにインターナルギヤの線上$${0min^{-1}}$$の所に点を打つ
サンギヤの線上$${1200min^{-1}}$$の所に点を打つ
2点を直線で結ぶ
キャリヤの線上にできた交点がキャリヤの回転速度を表す。
交点が水平線の反対側に現れたときは逆回転になります。

4速オートマチック・トランスミッション
4速オートマチック・トランスミッションの構造を考えるとき自動車整備士の問題を参考にするとわかりやすいです。
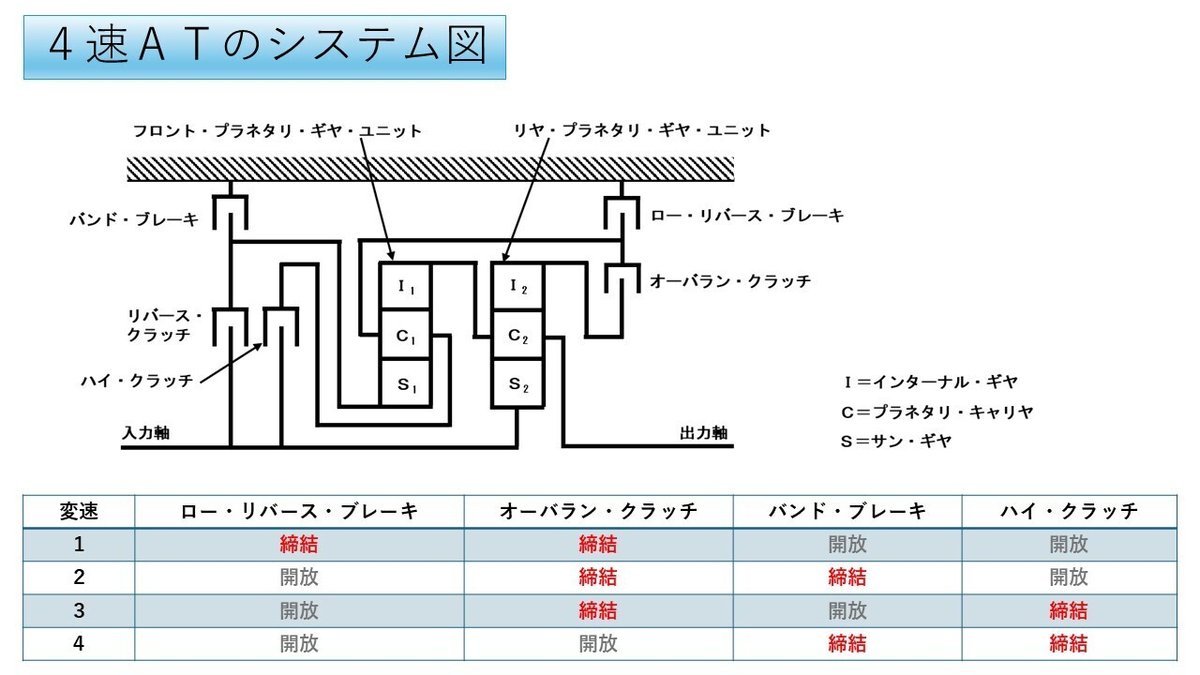
上図は4速オートマチック・トランスミッションの断面を表したものです。
1速の回転速度および変速比
まず、1速を考えてみましょう。
ここでは、サンギヤとインターナルギヤのギヤ比を1:2とし、入力軸の回転速度を$${1200min^{-1}}$$とします。

上図からI2は$${0min^{-1}}$$、S2は$${1200min^{-1}}$$のときC2の回転速度を求めたいので、速度線図を描くと下図になります。よって、C2に接続されている出力軸は$${400min^{-1}}$$となります。よって、変速比は1200/400=3.0です。

2速の回転速度および変速比
ここからプラネタリギヤが2段組み合わさったシステムの考え方になります。
2速のシステム図は下図の通りです。
ここで確認しておくことは、
・I1とC2が連結されている
・C1とI2が連結されている
ということです。

1段目のプラネタリギヤの速度線図を考えてみます
S1はバンド・ブレーキを介してケースに締結されているため回転速度が$${0min^{-1}}$$ということはわかります。しかし、C1とI1の回転速度はわかりません。

次に2段目のプラネタリギヤの速度線図を考えてみます。
S2は入力軸の回転速度になるので$${1200min^{-1}}$$となることはわかりますが、C2とI2の回転速度はわかりません。
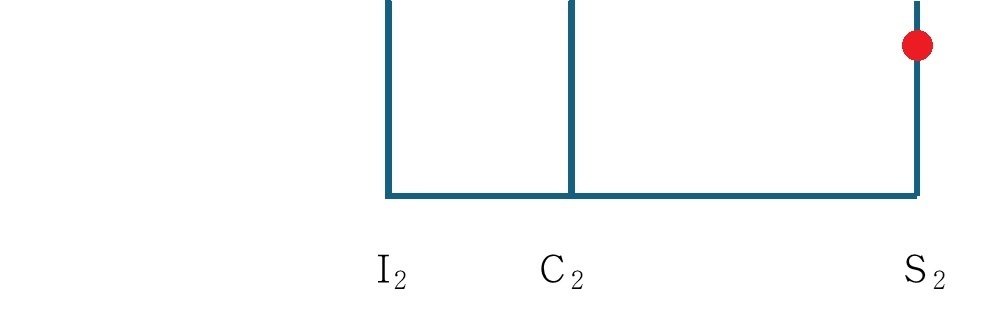
C1とI2、I1とC2は同じ回転速度になることがわかっているので上の2つの図を重ねることができます。

これを元に出力軸(C2)の回転速度を求めます。

S1からS2までは②+①+②=⑤の距離があり⑤で1200になるため①で1200/5=$${240min^{-1}}$$となります。
S1からC2までは③ありますので240×③=$${720min^{-1}}$$となります。
変速比は1200/720=1.67です。
3速の回転速度および変速比
3速も2速と同様に考えます。

3速の速度線図は以下のようになります。

これは至って簡単ですね。
まさに入力軸と出力軸が直結状態です。
出力軸の回転速度は$${1200min^{-1}}$$で変速比は1.0です。
4速の回転速度および変速比
下図は4速のときのシステム図です。


2速の速度線図とS2、I2の位置が逆になっていることに注意して下さい。
C2の回転速度は$${2100min^{-1}}$$となり、変速比は0.57となります。
まとめ
プラネタリギヤは数式で解こうとすると大変難解です。
しかし、速度線図を用いて系統的に説明すると理解し易いことがわかったと思います。
大学生のみなさん、高校生のみなさん、そして、高校生に教える先生方は是非、プラネタリギヤを理解してみて下さい。
高校の先生からは、そんなことは指導要領に含まれていないという人もいると思います。しかし、機械を教える者、携わる者としての基礎教養として如何でしょうか。機械要素の世界が少し広がると思います。
いいなと思ったら応援しよう!

