
バナッハ空間の定義と例
コラム
今回のコラムで紹介するのは、ポアンカレ予想に関してです。ポアンカレ予想の証明は筆者には難解すぎてとてもじゃないですが解説は不可能です(読んだこともありませんが)。なので、どのような主張であるかくらいは解説したいと思います。
(コラム書く方が楽しくなっているのはここだけの話。)
ポアンカレ予想
ポアンカレ予想とは次のような主張です。
ちなみに「予想」とは証明されていない主張のことを指します。ただし、ポアンカレ予想は証明されたため、「定理」ではありますが、名残でいまだにポアンカレ予想と呼ばれているような気がします(ポアンカレ定理と呼ばれているのは調べた限りでは見たことがありません)。
定理
$${M}$$を3次元閉多様体とする。
$$
\pi_1(M) \simeq \pi_1 (S^3) \Leftrightarrow M\simeq S^3\tag{1}
$$
ここで、$${S^3}$$は3次元球
$$
S^3=\{(x, y, z)\in\mathbb{R}^3 \mid x^2+y^2+z^3=1\}
$$
である。
(1)の左辺は群としての同型で、右辺は位相空間としての同相という意味です。ちなみに$${\Rightarrow}$$がポアンカレ予想の本質的な主張となっています。(可能な限り)この主張が理解できるよう一つ一つ概念を導入していきたいと思います。
ポアンカレ予想の歴史
ポアンカレ予想は1904年アンリ・ポアンカレという数学者によって提出されました。1900年ホモロジー群に関する予想として、
$$
H_1(M)\simeq H_1(S^3) \Leftrightarrow M\simeq S^3
$$
として提出していたようですが、ポアンカレ自身によって反例を見つけ、(1)の予想となったそうです。その後、100年もの間様々な数学者が解決しようとしましたが、部分的な解決もしくは同値条件の証明(これも反証されたようですが)の発見にとどまっています。
2000年アメリカのクレイ研究所から発表されたミレニアム懸賞問題の一つとしても指定されました。
ところが、2003年~2004年の間、グリゴリー・ペレリマンという数学者が突如としてポアンカレ予想を解いたという論文をarxivにプレプリントとして提出しました。
2006年まで、検証チームにより検証され、この証明に誤りがないことが分かり、ポアンカレ予想が解決しました。
ペレリマンの証明は、トポロジーではなく(トポロジー以前の)微分幾何学と物理学による証明であったことも面白い点です。
余談ですが、筆者は解決数年後、学生の頃にこの予想に関して知り、ジョージ・G・スピーロ著「ポアンカレ予想」にてよくわからないなりにわくわくしながら一連のできごとやトポロジーなどに関して学んだ記憶があります。
不変量と分類問題
筆者の理解では、ポアンカレ予想は不変量による分類問題であると理解しています。
分類問題とは、ある量に基づいて幾何学的対象を種類分けすることです。数学においては対象を分類することが主要な問題となっています。
(フィールズ賞を受賞した小平邦彦は、複素多様体の分類問題において重要な成果を残しているそうです。)
ある量として使われるのが不変量という考えです。
2つの幾何学的対象を$${S_1}$$と$${S_2}$$として、図形に対して決まる何かしらの量(整数、群、etc…)に対応させる関数を$${f}$$とすると、
$$
f(S_1) = f(S_2) \Leftrightarrow S_1 = S_2
$$
となるような$${f}$$を不変量といいます(より詳しく、完全不変量といいます)。
つまり、不変量$${f}$$が異なる図形は絶対に一致しないということが分かり、$${f}$$によって、図形同士が互いに種類分けされることとなります。
同相
(1)式の右辺に出現する、同相とは、位相空間として同値であるという概念で、全単射写像を用いて次のように定義されます。
定義
位相空間$${A}$$と$${B}$$の間の写像$${f}$$が同相写像であるとは、$${A}$$と$${B}$$の間の連続写像であり単射*かつ全射**なもので、さらにその逆写像も連続写像であり単射かつ全射なものである。
位相空間$${A}$$と$${B}$$の間に同相写像が存在するとき、$${A}$$と$${B}$$は同相であるという。
* $${f(x_1)=f(x_2)\Rightarrow x_1=x_2}$$が成り立つこと。
** 任意の$${y\in B}$$に対して、ある$${x\in A}$$が存在して、$${y=f(x)}$$となること。
簡単にいうと、位相構造も含めて同一視できるような位相空間同士のことを言います。
多様体
ポアンカレ予想の仮定の最初に出てきている多様体について説明します。
多様体は例えば、我々が立っている地面は平面のように見えますが、実は地球という球体の上に立っている、というように曲がっている曲面でもものすごく近づけば、平面のように見えるような図形、と筆者は理解しています。
ユークリッド幾何学から現代的な幾何学の理論へと発展させた考えと、筆者は思っています。歴史的にはベルンハルト・リーマンという数学者(これまたリーマン予想などで有名な数学者ですが)により、ゲッティンゲン大学の教職に就任するために行った講演「幾何学の基礎に関する仮説について」の中で提唱された概念です(昔読んでみましたが、あまりわからなかった記憶しかありません、当時は多様体という言葉は使っていなくて、$${n}$$重に広がった空間とかそんな言葉を使っていたような…)。
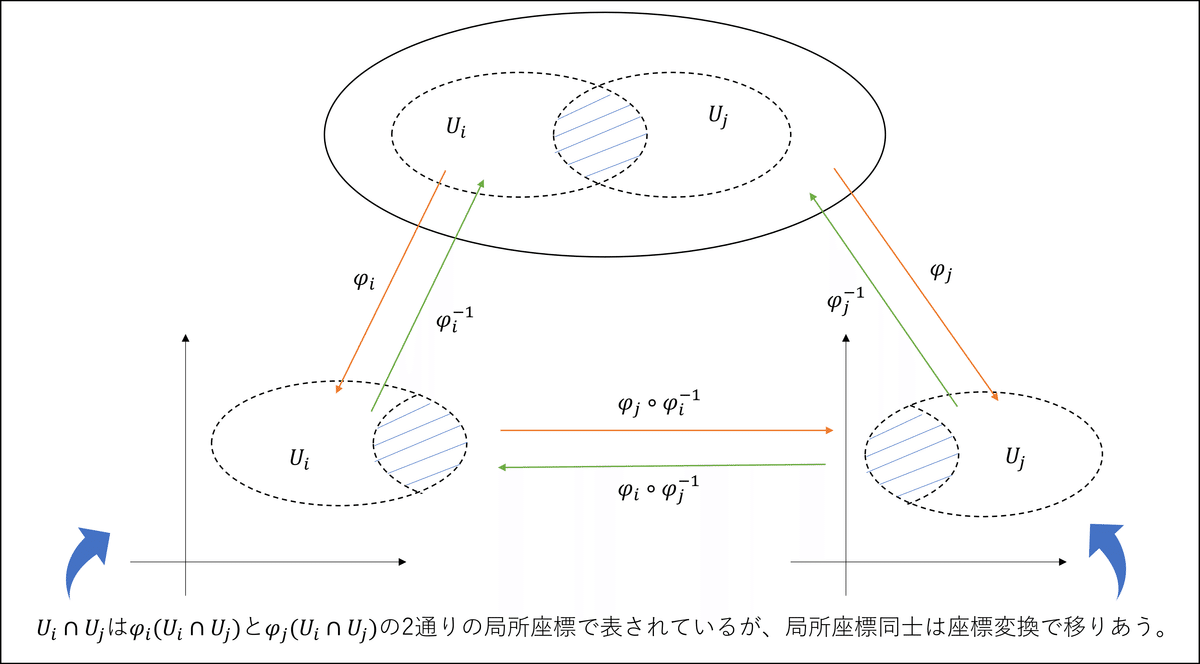
厳密には次のように同相写像と局所座標系による張り合わせ条件により記述されます。
定義
$${M}$$が$${n}$$次元多様体であるとは、$${M}$$がハウスドルフ空間であり、次のような近傍$${U_i}$$と、$${U_i}$$から$${n}$$次元ユークリッド空間の開集合への同相写像$${\varphi_i: U_i\rightarrow \varphi_i(U_i)\subset \mathbb{R}^n}$$が存在することである。
$$
\bigcup_{i} U_i=M
$$
$${U_i\cap U_j\neq\empty}$$のとき
$$
\varphi_i\circ \varphi_j^{-1}|_{\varphi_j(U_i\cap U_j)} : \varphi_j(U_i\cap U_j)\rightarrow \varphi_i (U_i\cap U_j)
$$
が$${C^\infty}$$級(無限回部分可能)である。
$${a\in M}$$に対し、$${\varphi_i(a)}$$を$${a}$$の局所座標という。
基本群
先程、ポアンカレ予想は不変量による分類問題といいましたが、ここで不変量として採用されているのが、基本群と呼ばれる群です。これが式(1)の左辺に表れている$${\pi_1}$$のことです。
基本群を定義します。
$${X}$$を位相空間とします。$${\lbrack 0, 1\rbrack}$$から$${X}$$への連続写像$${f}$$をパスと呼びます。イメージとしては、$${X}$$の上の曲線ということです。
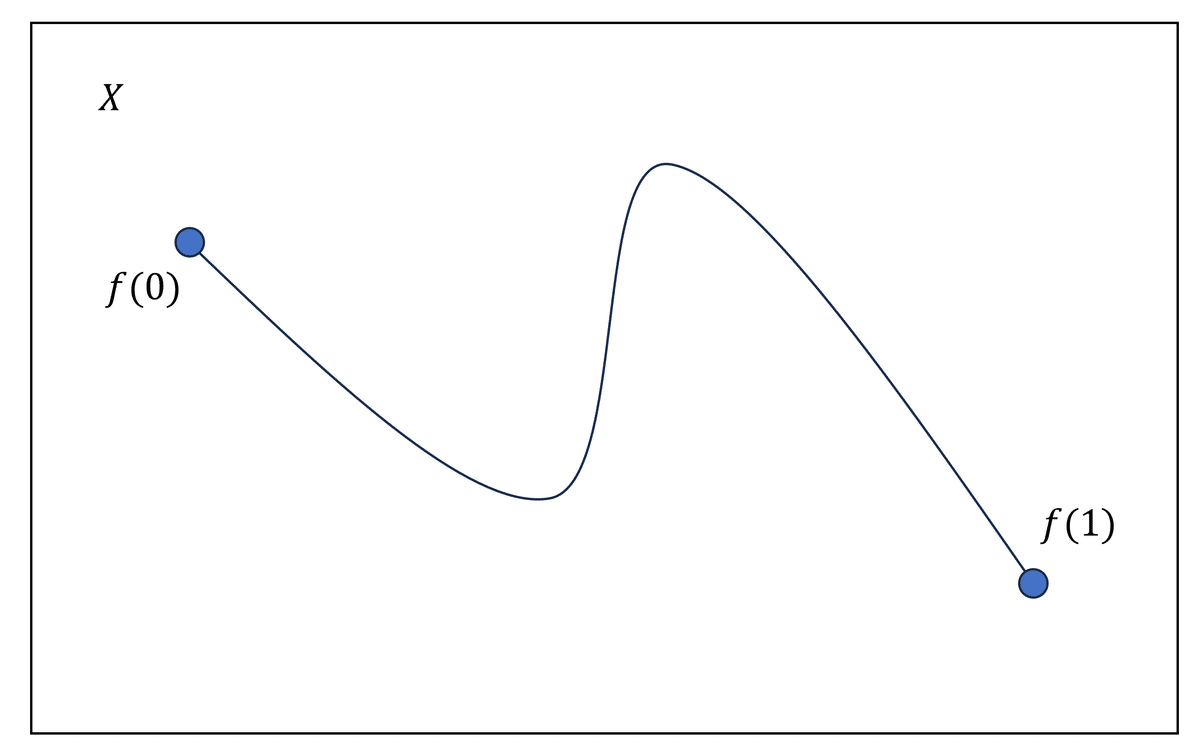
定義(パスのホモトピー)
パスのホモトピーとは、連続写像の族$${\{f_t:\lbrack 0,1 \rbrack \rightarrow X\}_{t\in \lbrack 0,1 \rbrack}}$$ で次の条件を満たすものである。
任意の$${t\in \lbrack 0,1 \rbrack}$$に対して、$${f_t(0)=x_0}$$、$${f_t(1)=x_1}$$
$${F:\lbrack 0,1 \rbrack\times \lbrack 0,1 \rbrack\rightarrow X}$$を$${F(s,t)=f_t(s)}$$と定義すると、$${F}$$は連続。

定義
2つのパス$${f^\prime}$$、$${f^{\prime\prime}}$$をつなぐホモトピー$${f_t \ \ (f_0=f^{\prime}, f_1=f^{\prime\prime})}$$が存在するとき、$${f^{\prime}}$$と$${f^{\prime\prime}}$$はホモトープといい、$${f^{\prime}\simeq f^{\prime\prime}}$$で表す。この$${\simeq}$$は同値関係となる(つまり反射律、対称律、推移律を満たす)。
パス$${f}$$の$${\simeq}$$による同値類を$${f}$$のホモトピー類といい、$${\lbrack f \rbrack}$$で表す。
ホモトピー類の集合は群となり(つまり演算構造が存在)、それを基本群といいます。以下それを厳密に述べます。
定義(パスの積)
$${f,g:\lbrack 0,1 \rbrack\rightarrow X}$$を、$${f(1)=g(0)}$$を満たすパスとする。次で定義されるパス$${f\cdot g: \lbrack 0,1 \rbrack\rightarrow X}$$を$${f}$$と$${g}$$の合成という。
$$
f\cdot g(s)=
\begin{cases}
f(2s) \ \ (0\le s\le 1/2) \\
g(2s-1) \ \ (1/2 \le s \le 1)
\end{cases}
$$
定義(ループ)
$${x_0}$$を起点とするループとは、パス$${f:\lbrack 0,1 \rbrack\rightarrow X}$$で$${f(0)=f(1)=x_0}$$を満たすものである。
ループはパスのうち、始点と終点が一致するぐるっとわっかになった経路のことです(わかると思いますが、少し大事なことなので、改めて記載)。
$${x_0\in X}$$に対し、
$$
\pi_1(X, x_0)=\{\lbrack f \rbrack\ \mid fはx_0を起点とするループ\}
$$
と定義する。$${\pi_1(X, x_0)}$$に積$${\cdot}$$を
$$
\lbrack f \rbrack \cdot \lbrack g \rbrack = \lbrack f\cdot g \rbrack
$$
と定義するとこれはwell-defined(代表元の取り方に依存せずに同値類が一意に定まる)。
この証明としては、$${f\simeq f^{\prime}}$$、$${g\simeq g^{\prime}}$$として、$${f}$$と$${f^{\prime}}$$をつなぐホモトピーを$${f_t}$$、$${g}$$と$${g^{\prime}}$$をつなぐホモトピーを$${g_t}$$とすると、$${f_t\cdot g_t}$$は$${f\cdot g}$$と$${f^{\prime}\cdot g^{\prime}}$$をつなぐホモトピーであるので成り立ちます。
つまり、積$${\cdot}$$は$${\pi_1(X,x_0)}$$の上での2項演算となる。
定理
$${\pi_1(X,x_0)}$$は積$${\cdot}$$の下で群になる。$${\pi_1(X, x_0)}$$を起点とする$${X}$$の基本群という。
群の3条件(単位元の存在、結合律の成立、逆元の存在)を満たすことを証明すれば大丈夫です。
まず最初に準備として、$${\varphi(0)=0, \varphi(1)=1}$$を満たすような連続写像$${\varphi:\lbrack 0,1 \rbrack\rightarrow \lbrack 0,1 \rbrack}$$について、$${\lbrack f\circ \varphi \rbrack=\lbrack f \rbrack}$$が成り立つ。実際、ホモトピーを$${(f\circ \varphi)_t=f\circ((1-t)\varphi+t\mathbf{1}_{\lbrack 0,1 \rbrack})}$$と定義すると、$${f\circ \varphi}$$と$${f}$$をつなぐホモトピーとなります。
単位元の存在を証明します。定数関数$${c:\lbrack 0,1 \rbrack\rightarrow X}$$を$${c(s)=x_0 \ (s\in S)}$$で定義すると、$${\lbrack c \rbrack}$$が単位減となります。実際、$${\varphi:\lbrack 0,1 \rbrack\rightarrow \lbrack 0,1 \rbrack}$$を
$$
\varphi(s)=
\begin{cases}
0 \ \ (0\le s\le 1/2) \\
2(s-1/2) \ \ (1/2\le s\le 1)
\end{cases}
$$
として、任意のループ$${f}$$を考えると、
$$
f\circ \varphi(s)=
\begin{cases}
f(0)=x_0 \ \ (0\le s\le 1/2) \\
f(2s-1) \ \ (1/2\le s\le 1)
\end{cases}
$$
$$
c\cdot f(s)=
\begin{cases}
c(2s)=x_0 \ \ (0\le s\le 1/2) \\
f(2s-1) \ \ (1/2\le s\le 1)
\end{cases}
$$
なので、$${f\simeq f\circ\varphi=c\cdot f}$$より$${\lbrack f \rbrack=\lbrack c \cdot f \rbrack=\lbrack c \rbrack\cdot \lbrack f \rbrack}$$となります。
また、
$$
\varphi^{\prime}(s)=
\begin{cases}
2s \ \ (0\le s\le 1/2) \\
1 \ \ (1/2\le s\le 1)
\end{cases}
$$
とすれば、
$$
f\circ \varphi^{\prime}(s)=
\begin{cases}
f(2s) \ \ (0\le s\le 1/2) \\
f(1)=x_1 \ \ (1/2\le s\le 1)
\end{cases}
$$
$$
f\cdot c(s)=
\begin{cases}
f(2s) \ \ (0\le s\le 1/2) \\
c(2s-1)=x_1 \ \ (1/2\le s\le 1)
\end{cases}
$$
なので、$${f\simeq f\circ\varphi^{\prime}=f\cdot c}$$より$${\lbrack f \rbrack=\lbrack f \cdot c \rbrack=\lbrack f \rbrack\cdot \lbrack c \rbrack}$$となります。
次に結合律を示します。任意のループ$${f,g,h}$$について$${\lbrack f\cdot (g\cdot h) \rbrack = \lbrack (f\cdot g)\cdot h \rbrack}$$を示せばよい。ループの積の定義より、
$$
((f\cdot g)\cdot h)(s)=
\begin{cases}
f(4s) \ \ (0\le s\le 1/4) \\
g(4s-1) \ \ (1/4\le s \le 1/2) \\
h(2s-1) \ \ (1/2 \le s\le 1)
\end{cases}
$$
$$
(f\cdot (g\cdot h))(s)=
\begin{cases}
f(2s) \ \ (0\le s\le 1/2) \\
g(4s-2) \ \ (1/2\le s \le 3/4) \\
h(4s-3) \ \ (3/4 \le s\le 1)
\end{cases}
$$
となります。$${F:\lbrack 0,1 \rbrack\times \lbrack 0,1 \rbrack\rightarrow X}$$を
$$
F(s,t)=
\begin{cases}
f(\frac{4s}{1+t}) \ \ 0\le s\le \frac{t+1}{4} \\
g(4s-(1+t)) \ \ \frac{t+1}{4}\le s\le \frac{t+2}{4} \\
h(\frac{4s-(2+t)}{2-t}) \ \ \frac{t+2}{4}\le s\le 1
\end{cases}
$$
とすれば、
$$
F(s, 0)=(f\cdot g)\cdot h))(s)
$$
$$
F(s,1)=(f\cdot (g\cdot h))(s)
$$
より、$${F}$$は$${(f\cdot g)\cdot h}$$と$${f\cdot (g\cdot h)}$$のホモトピーである。
最後に逆元の存在を証明する。$${\bar{f}:\lbrack 0,1 \rbrack\rightarrow X}$$を$${\bar{f}(s)=f(1-s)}$$とする。
$$
(f\cdot \bar{f})(s)=
\begin{cases}
f(2s) \ \ 0\le s\le \frac{1}{2} \\
f(2s-2) \ \ \frac{1}{2} \le s\le 1
\end{cases}
$$
より、
$${F:\lbrack 0,1 \rbrack\times \lbrack 0,1 \rbrack\rightarrow X}$$を
$$
\begin{cases}
f(2s) \ \ (0\le s\le \frac{1-t}{2}, 0\le t<1) \\
f(1-t) \ \ (\frac{1-t}{2}\le s\le \frac{1+t}{2}, 0\le t<1) \\
f(2-2s) \ \ (\frac{1+t}{2}\le s \le 1, 0\le t<1) \\
c(s) \ \ t=1
\end{cases}
$$
とすると、
$$
F(s, 0)=(f\cdot \bar{f})(s)
$$
$$
F(s,1)=c(s)
$$
より、$${F}$$は$${f\cdot \bar{f}}$$と$${c}$$のホモトピーであり、$${\bar{f}}$$が逆元となる。
位相空間$${X}$$が弧状連結(任意の2点を曲線でつなぐことができる)の場合、基点に依らず基本群が同型であることが証明できるため、基点を省略して、$${\pi_1(X)}$$と書きます。
ポアンカレ予想(再考)
以上でポアンカレ予想の主張を理解するための概念はそろったと思います。改めて、主張をもう一度見てみましょう。
定理
$${M}$$を3次元閉多様体とする。
$$
\pi_1(M) \simeq \pi_1 (S^3) \Leftrightarrow M\simeq S^3
$$
3次元多様体が3次元球の基本群と異なれば、それは決して同相とはならない、つまり位相としては3次元球とは全く異なった種類の位相をもつ、ということがわかります。
もっと壮大な使用例を述べます。実は$${\pi_1(S^3)}$$は計算することが可能で、3次元球上のループは必ず手繰り寄せて1点にすることができるため、基本群としては単位元のみからなる自明な群となります。
$$
\pi_1(S^3)\simeq \{e\}
$$
宇宙(月とか地球とか浮いてるあれです)の形状を表す3次元多様体を$${M}$$とします。
もしもできるのなら、宇宙をくまなくループで埋め尽くすことができたとしましょう。
もし、埋め尽くしたループをすべて手繰り寄せることができたのならば、この世界に存在する宇宙の形は、球である、ということがいうことができます。
逆にどこかしらで引っかかって、手繰り寄せられないループが存在したのならば、宇宙はもっと別な形、例えばドーナツ型(数学では普通トーラスといいます)ということになります。
上の話は、宇宙をくまなくループで埋め尽くせたら、の話なので実践可能かどうかはまた別な話です。しかし、理論とはこういった夢の大きな話まで容易にたどり着けてしまう魅了溢れるものと思います。
はじめに
今回はバナッハ空間について述べたいと思います。
ちなみにバナッハ空間は、ステファン・バナッハという数学者により、博士論文である「抽象集合の演算とその積分方程式への応用について」で提唱された概念だそうです。現代の関数解析学の基礎として高く評価されています。
ノルム空間
ノルム空間の定義
定義(ベクトル空間)
$${S}$$ を空でない集合とする。 $${S}$$ における加法 $${S\times S\rightarrow S:(x,y)\mapsto x+y}$$ と スカラー倍法 $${\mathbb{R}\times S\rightarrow S:(\lambda, x)\mapsto \lambda x}$$ とが与えられ、次の1. と2. が満たされるとき、 $${S}$$ はこれらの演算に関してベクトル空間であるという。
加法について
(1) 任意の $${x,y\in S}$$ に対して、 $${x+y=y+x}$$
(2) 任意の $${x,y,z\in S}$$ に対して、$${(x+y)+z=x+(y+z)}$$
(3) $${S}$$ に一つの元 $${0}$$($${S}$$ の零元と呼ばれる) があって、$${S}$$ のすべての元$${x}$$に対して、$${x+0=x}$$が成り立つ。
(4) $${S}$$ の任意の元 $${x}$$ に対し、 $${x+(-x)=0}$$ となる $${S}$$ の元 $${-x}$$ が存在する。スカラー倍法(と加法)について
(1) 任意の$${x,y\in S}$$ 、 任意の$${\lambda\in\mathbb{R}}$$ に対して、 $${\lambda(x+y)=\lambda x + \lambda y}$$ 。
(2) 任意の $${x\in S}$$ 、 任意の$${\lambda, \mu \in \mathbb{R}}$$ に対して、$${(\lambda +\mu)x=\lambda x + \mu x}$$ 。
(3) 任意の$${x\in S}$$ 、任意の$${\lambda, \mu \in \mathbb{R}}$$に対して、$${(\lambda\mu)x=\lambda(\mu x)}$$ 。
(4) 任意の$${x\in S}$$ に対して、$${1x=x}$$ ($${1}$$は実数$${1}$$である。)
$${\mathbb{R}}$$ の代わりに $${\mathbb{C}}$$ にしたものを、複素ベクトル空間という。
いま、 $${S}$$ を一つのベクトル空間とし、 $${\varphi}$$ を $${S}$$ から、 $${\mathbb{R}}$$ への一つの写像とする。ただし、 $${x\in S}$$ の $${\varphi}$$ による像 $${\varphi(x)}$$ をここでは $${|x|}$$ と書くことにする。これについて、次の $${(N1)}$$~$${(N4)}$$ が成り立つとき、 $${\varphi=| \ |}$$ を $${S}$$ 上のノルムという。
(N1) 任意の $${x\in S}$$ に対して $${|x|\ge 0}$$ 。
(N2) $${|x|=0}$$ となるのは $${x=0}$$ のとき、またそのときに限る。
(N3) 任意の $${x\in S}$$ 、任意の $${\lambda\in\mathbb{R}}$$ に対して、 $${|\lambda x|=|\lambda||x|}$$ 。
(N4) 任意の $${x,y\in S}$$ に対して、 $${|x+y|\le |x|+|y|}$$ 。
ベクトル空間$${S}$$の上に一つのノルム$${| \ |}$$ が与えられたとき、$${S}$$と$${| \ |}$$ の組$${(S, ||)}$$ をノルム空間という。
ノルム空間$${S}$$の2点 $${x,y}$$ に対し、
$$
d(x,y)=|x-y|
$$
とおく。この $${d}$$ をノルム $${| \ |}$$ から定められる距離関数といい、 $${d(| \ |)}$$ で表す。
ノルム空間の例
例1.
集合 $${\mathbb{R}^n}$$ において、その2点 $${x=(x_1,\dots, x_n)}$$ , $${y=(y_1\dots, y_n)}$$ に対し
$$
x+y = (x_1 + y_1,\dots, x_n + y_n)
$$
また、 $${\mathbb{R}^n}$$ の点 $${x=(x_1, \dots, x_n)}$$ と $${\lambda\in \mathbb{R}}$$ に対し、
$$
\lambda x = (\lambda x_1,\dots, \lambda x_n)
$$
と定義すれば、 $${\mathbb{R}^n}$$ はこれらの算法に関して( $${\mathbb{R}}$$ 上の)ベクトル空間になる。さらにこのベクトル空間において、 $${x=(x_1,\dots, x_n)}$$ に対し、
$$
|x|^{(n)}=\sqrt{\displaystyle\sum_{i=1}^{n} x_i^2}
$$
と定めれば、 $${| \ |^{(n)}}$$ は $${\mathbb{R}^n}$$ 上の一つのノルムとなる。
例2.
ベクトル空間 $${\mathbb{R}^n}$$ において、 $${x=(x_1,\dots, x_n)}$$ に対し、
$$
|x|_1^{(n)}=\displaystyle\sum_{i=1}^n |x_i|
$$
$$
|x|_{\infty}^{(n)}={\rm{max}}\{|x_1|,\dots, |x_n|\}
$$
とおけば、これらも $${\mathbb{R}^n}$$ 上のノルムとなる。
例3.
$${\mathbb{R}^{\mathbb{N}}}$$ の元、すなわち実数の無限列 $${(x_n){n\in\mathbb{N}}=(x_1,x_2,\dots,x_n,\dots)}$$ で、級数 $${\displaystyle\sum_{n=1}^{\infty} x_n^2}$$ が収束する( $${\displaystyle\sum_{n=1}^{\infty} x_n^2<+\infty}$$ )ものを考え、そのような無限列全体の集合を $${l^{(2)}}$$ とする。 $${l^{(2)}}$$ の元 $${x=(x_n){n\in\mathbb{N}}}$$ 、 $${y=(y_n){n\in\mathbb{N}}}$$ および 実数 $${\lambda}$$を
$$
x+y = (x_n + y_n), \ \ {n\in\mathbb{N}}, \ \ \lambda x = (\lambda x_n), \ \ {n\in\mathbb{N}}
$$
と定義すれば、 $${\displaystyle\sum_{n=1}^{\infty}(x_n+y_n)^2\le 2\left(\displaystyle\sum_{n=1}^{\infty}x_n + \displaystyle\sum_{n=1}^{\infty}y_n\right) <+\infty}$$ 、 $${\displaystyle\sum_{n=1}^{\infty}(\lambda x_n)^2=\lambda^2 \displaystyle\sum_{n=1}^{\infty}x_n^2 < +\infty}$$ であるから、 $${x+y}$$ と $${\lambda x}$$ も $${l^{(2)}}$$ の元となる。 これらの算法に関して、 $${l^{(2)}}$$ はベクトル空間となる。
また、 $${l^{(2)}}$$ の元 $${x=(x_n){n\in\mathbb{N}}}$$ に対し、
$$
|x| = \sqrt{\displaystyle\sum_{n=1}^{\infty} x_n^2}
$$
と定める。これはノルムの性質(N1)~(N3)を満たす。また、 $${\mathbb{R}^k}$$ におけるノルムの性質 $${| \ |^{(k)}}$$ の性質
$$
\sqrt{\displaystyle\sum_{n=1}^k (x_n + y_n)^2}\le \sqrt{\displaystyle\sum_{n=1}^k x_n^2} + \sqrt{\displaystyle\sum_{n=1}^k y_n^2}
$$
において、 $${k\rightarrow \infty}$$ とすれば
$$
|x+y| \le |x|+|y|
$$
が得られる。 よって、 $${(l^{(2)}, | \ |)}$$ はノルム空間となる。このノルム空間を Hilbert空間または $${l^{(2)}}$$ 空間という。
例4.
$${X}$$ を空でない任意の集合とし、 $${X}$$ 上の有界実数値関数全体の集合を $${S^*=\mathscr{F}^b(X, \mathbb{R})}$$ とする。 $${f, g\in S^*}$$ 、 $${\lambda\in\mathbb{R}}$$ に対し、 $${X}$$ から $${\mathbb{R}}$$ への写像 $${f+g}$$ 、 $${\lambda f}$$ を
$$
(f+g)(x)=f(x)+g(x), \ \ (\lambda f)(x) = \lambda f(x) \ \ (x\in X)
$$
と定義すれば、これらも $${X}$$ 上の有界実数値関数、すなわち $${S^*=\mathscr{F}^b(X, \mathbb{R})}$$ の元である。 この加法とスカラー倍について、 $${S^*}$$ はベクトル空間をなす。
$${f\in S^*}$$ に対し、
$$
|f|={\rm{sup}}\{|f(x)| : x\in X\}
$$
と定める。
$${X}$$ が位相空間であるとき、 $${X}$$ 上の実数値関数で有界かつ連続であるもの全体の集合を $${B(X, \mathbb{R})}$$ で表す。これを $${S}$$ とすれば、 $${S\subset S^=\mathscr{F}^b(X, \mathbb{R})}$$であるが、 $${f, g\in S}$$ ならば、 $${f+g, \lambda f\in S}$$ である(連続関数の和もスカラー倍も連続関数)から、 $${S}$$ もまたベクトル空間 (部分空間) である。 $${S^*}$$ のノルムを $${S}$$ 上で制限すれば、 $${S}$$ 上のノルムが得られるから、 $${S}$$ もノルム空間である。
バナッハ空間
完備性
定義
$${(S, d)}$$ を距離空間とする。 $${S}$$ の点列 $${(a_n)_{n\in \mathbb{N}}}$$ は、次の性質を満足するとき、コーシー列であるといわれる。
任意に正数 $${\epsilon}$$ を与えたとき、 適当に自然数 $${n_0}$$ をとれば、 $${m>n_0}$$ 、 $${n>n_0}$$ であるすべての自然数 $${m,n}$$ に対して、 $${d(a_m, a_n)<\epsilon}$$ が成り立つ。
収束点列はコーシー列であるが、逆が成り立つとは限らない。
例.1
$${\mathbb{R}}$$ の開区間 $${(0,1)}$$ を $${S}$$ とする。 $${S}$$ において、点列
$$
\frac{1}{2}, \frac{1}{3},\dots, \frac{1}{n}
$$
は Causy点列であるが、収束点列ではない。実際、十分大きい $${m}$$ に対して、 $${\frac{1}{m}<\epsilon/2}$$ 、 $${\frac{1}{n}<\epsilon/2}$$ とできるので、
$$
d(\frac{1}{m}, \frac{1}{n}) \le d(\frac{1}{m}, 0) + d(0, \frac{1}{n}) < \epsilon
$$
しかし、 $${0\notin S}$$ より、収束点列ではない。
定義
距離空間 $${(S, d)}$$ において、その任意のコーシー列が収束するとき $${(S, d)}$$ は完備であるという。
バナッハ空間の定義と例
定義
ノルム空間 $${(S, | \ |)}$$ は、 $${| \ |}$$ から定められる距離関数 $${d=d(| \ |)}$$ に関して $${(S, d)}$$ が完備(コーシー列が必ず収束する)であるとき、Banach空間であるという。
定理
Hilbert空間 $${l^{(2)}}$$ はBanach空間である。
証明) $${l^{(2)}}$$ のノルム $${| \ |}$$ から定められる距離関数を $${d}$$ とし、$${(x^{(k)})_{k\in\mathbb{N}}}$$ を距離空間 $${(l^{(2)}, d)}$$ における任意のコーシー列とする。これが収束することを示せばよい。
$${x^{(k)}=(x^{(k)}n){n\in\mathbb{N}}=(x^{(k)}_1,x^{(k)}_2,\dots,x^{(k)}n,\dots)}$$ とする。一つの自然数 $${n}$$ を任意に固定するとき、ノルム $${| \ |}$$ の定義から、任意の $${k,l\in\mathbb{N}}$$ に対し、
$$
|x^{(k)}_n - x^{(l)}_n|\le |x^{(k)}_n - x^{(l)}_n|=d(x^{(k)}, x^{(l)})
$$
この不等式と、 $${(x^{(k)})_{k\in\mathbb{N}}}$$ が $${l^{(2)}}$$ のコーシー列であることから、 $${(x^{(k)}n)_{k\in\mathbb{N}}}$$ は $${\mathbb{R}}$$ のコーシー列であることがわかる。したがって、 $${\mathbb{R}}$$ の完備性により、 $${\mathbb{R}}$$ の元$${x_n=\displaystyle\lim_{k\rightarrow\infty} x^{(k)}_n}$$ が存在する。 そこで、 $${x=(x_n), \ \ {n\in\mathbb{N}}}$$ とおく。この $${x}$$ が $${l^{(2)}}$$ に属し、かつ $${l^{(2)}}$$ において、 $${\displaystyle\lim_{k\rightarrow\infty} x^{(k)}=x}$$ となることを示す。
$${\epsilon}$$ を任意の正数とすれば、 $${(x^{(k)})_{k\in\mathbb{N}}}$$ は $${l^{(2)}}$$ のコーシー列であるから、ある $${k_0\in\mathbb{N}}$$ が存在して、 $${k,l>k_0}$$ である任意の $${k,l\in\mathbb{N}}$$ に対して
$$
d(x^{(k)}, x^{(l)})=|x^{(k)} - x^{(l)}|<\epsilon
$$
すなわち、
$$
\displaystyle\sum_{n=1}^\infty (x^{(k)}_n - x^{(n)}_n)^2 <\epsilon^2
$$
が成り立つ。よって $${h}$$ を任意の自然数とすれば
$$
\displaystyle\sum_{n=1}^h (x^{(k)}_n - x^{(n)}_n)^2 <\epsilon^2
$$
上式で、 $${l\rightarrow\infty}$$ とすれば、 $${x^{(l)}_n\rightarrow x_n}$$ であるから、
$$
\displaystyle\sum_{n=1}^h (x^{(k)}_n - x_n)^2 \le \epsilon^2\tag{2}
$$
となる。そこで、
$$
x_n^2 =(x^{(k)}_n-(x^{(k)}n -x_n))^2\le 2((x^{(k)}n)^2+(x^{(k)}n-x_n)^2)
$$
に注意すれば、 $${\displaystyle\sum_{n=1}^\infty (x^{(k)}_n)^2 < +\infty}$$ であるから、(2)式より、
$$
\displaystyle\sum_{n=1}^\infty x_n^2 \le 2(|x^{(k)}|^2+\epsilon^2) < +\infty
$$
ゆえに、 $${x=(x_n)_{n\in\mathbb{N}}\in l^{(2)}}$$ である。また、 (2)式から、
$$
d(x^{(k)}, x)=|x^{(k)}-x|\le \epsilon
$$
これが、 $${k>k_0}$$ であるすべての$${k\in\mathbb{N}}$$ に対して成り立つから、
$$
\displaystyle\lim_{k\rightarrow\infty}x^{(k)}=x
$$
となる。
定理
$${X}$$ を任意の集合とするとき、ノルム空間$${\mathfrak{F}^b(X, \mathbb{R})}$$ (有界実数値関数の全体) はBanach空間である。
証明) $${(f_n){n\in\mathbb{N}}}$$ を $${S^*=\mathfrak{F}^b(X,\mathbb{R})}$$ の任意のCauchy点列とする。ノルムの性質から、
$$
||f_m|-|f_n||\le|f_m-f_n|
$$
であるから、実数列は $${(|f_n|)_{n\in\mathbb{N}}}$$ は $${\mathbb{R}}$$ のコーシー列で、したがって有界である(参考: https://kaikiblog.com/cauchy_bounded/)。すなわち、適当な正の実数 $${K}$$ をとれば、すべての $${n\in\mathbb{N}}$$ に対して $${|f_n|\le K}$$ が成り立つ。一方、 $${X}$$ の点 $${x}$$ を任意に固定するとき、 $${S^*}$$ におけるノルムの定義により、
$$
|f_m(x)-f_n(x)|\le \|f_m-f_n\|
$$
であるから、 $${(f_n(x)){x\in\mathbb{N}}}$$ も $${\mathbb{R}}$$ のコーシー列である。したがって、 $${\displaystyle\lim_{n\rightarrow\infty} f_n(x)}$$ が存在する。それを$${f(x)}$$ として $${f:X\rightarrow\mathbb{R}}$$ を定義すれば、 $${f\in S^*}$$ で、 $${S^*}$$ において、 $${\displaystyle\lim_{n\rightarrow\infty} f_n=f}$$ となることを示す。
まず、$${X}$$ の任意の点 $${x}$$ と任意の正数 $${\epsilon}$$ に対し、$${n}$$ を十分大きくとれば、$${|f_n(x)-f(x)|<\epsilon}$$ が成り立つから、
$$
|f(x)|<|f_n(x)|+\epsilon \le |f_n| +\epsilon \le K+\epsilon
$$
したがって、$${f}$$ は$${X}$$ 上の有界実数値関数、すなわち $${\mathfrak{F}^b(X,\mathbb{R})=S^*}$$ の元である。
また、任意に$${\epsilon >0}$$ を与えるとき、適当に$${n_0}$$ をとれば、 $${m,n>n_0}$$ である任意の$${m,n\in\mathbb{N}}$$ に対して$${|f_n-f_m|<\epsilon}$$ であるから、$${X}$$ のどの点 $${x}$$ についても $${|f_n(x)-f_m(x)|<\epsilon}$$ 。この不等式で $${m\rightarrow\infty}$$ とすれば、 $${|f_n(x)-f(x)|\le\epsilon}$$ 。これがすべての $${x\in X}$$ に対して成り立つから、
$$
|f_n-f|\le\epsilon
$$
ゆえに、 $${\displaystyle\lim_{n\rightarrow\infty} f_n=f}$$ 。
定理
$${X}$$ を任意の位相空間とするとき、 $${B(X,\mathbb{R})}$$ はBanach空間である。
証明) $${(f_n){n\in\mathbb{N}}}$$ を$${S=B(X,\mathbb{R})}$$ のコーシー列とする。上の定理からこれが$${S^*}$$ の中では極限を持つことは証明されているので、それが$${S}$$ に属すること、すなわち $${X}$$ 上で連続であることを証明すればよい。
$${a}$$を$${X}$$ の任意の1点、$${\epsilon}$$ を任意の正数とする。 $${\displaystyle\lim_{n\rightarrow\infty}f_n=f}$$ すなわち、 $${\displaystyle\lim_{n\rightarrow\infty}|f_n-f|=0}$$ であるから、適当な $${n_o\in\mathbb{N}}$$ をとれば、
$$
|f_n-f|<\frac{\epsilon}{3}\tag{3}
$$
が成り立つ。また、 $${f_{n_0}}$$ は連続であるから、 $${a}$$ の適当な近傍 $${U}$$ をとれば、任意の$${x\in U}$$ に対して、
$$
|f_{n_0}(x)-f_{n_0}(a)| < \frac{\epsilon}{3}
$$
となる。また、(3)式により、
$$
|f_{n_0}(x)-f(x)| < \frac{\epsilon}{3}, \ \ |f_{n_0}(a)-f(a)| < \frac{\epsilon}{3}
$$
であるから、 $${x\in U}$$ ならば、
$$
|f(x)-f(a)|\le |f(x)-f_{n_0}(x)|+|f_{n_0}(x)-f_{n_0}(a)|+|f_{n_0}(a)-f(a)| \
<\frac{\epsilon}{3}+\frac{\epsilon}{3}+\frac{\epsilon}{3}=\epsilon
$$
ゆえに、 $${f:X\rightarrow \mathbb{R}}$$ である。
位相空間$${X}$$ 上の実連続関数全体の集合を$${C(X,\mathbb{R})}$$と書く。 $${X}$$ がコンパクト*な位相空間である場合、$${X}$$ 上の実連続関数は有界となる。したがって、$${C(X,\mathbb{R})=B(X,\mathbb{R})}$$ となる。 ゆえに、上の定理から次の系が得られる。
* 任意の解被覆に対して、有限個の開集合を取り出して再び覆うことができる性質。単に有限個の開集合で覆うことができる、というわけではないことは間違えやすいので注意。
系
$${X}$$ を任意のコンパクトな位相空間とするとき、 $${C(X,\mathbb{R})}$$ はBanach空間である。
おわりに
ポアンカレ予想の解決は、ミレニアム問題の一つの解決であり、ここ最近では数学の大きな動きと思います。人づてではありましたが、筆者も当時そのような大きな問題が解かれたと聞いて、わくわくした思い出があります。その後もABC予想の解決など、大きな問題の解決を目の当たりにできる時代に生きているのは幸運なのかな、と思いました。
参考
[1] 丸山徹, "群上の調和解析", 丸善出版, 2023
[2] 松坂和夫, "集合・位相入門", 岩波書店, 1968(初版)
[3] 小沢誠, "ポアンカレ予想"
[4] 平井広志, "幾何数理工学ノート 位相幾何:基本群"
[5] 今泉 拓巳, "Seifert-van Kampen の定理と 位相空間の基本群"
