AtCoder Beginner Contest 304 A-EをTypeScriptで解く。

先週に引き続きAtCoder Beginner Contest 304に参加をした。
コンテスト自体はPythonで参加をしたのだけど、Typescriptで振り返り記事を書く。

結果

A,B,C,D,Eのノーペナ５完。
今回は判定の遅れが発生しコンテストを20分延長するものの、unratedとなってしまった。順位は1,500位前後と自分の中では好成績だったので、残念だった。気を取り直して、振り返る。

A - First Player

A - First Player

二人以上のN人が時計回りに円卓に座っている。
それぞれの名前と年齢が与えられるので、年齢が一番低い人を起点として、時計回りでN人の名前を出力する問題。

ちょっとA問題にしては難しいと思った。
一番低い年齢を調べてそこからfor loopを回す。インデックスで余りを取る。

import { createInterface } from "readline";
import * as fs from "fs";
import { log } from "console";
import { exit } from "process";

function main() {
    const n = nextNum()
    // 最少の年齢
    let minAge = 10 ** 10
    type person = [string, number]
    const persons: person[] = []
    for (let i = 0; i < n; i++) {
        const name = next()
        const age = nextNum()
        minAge = Math.min(minAge, age)
        persons.push([name, age])
    }
    for (let i = 0; i < n; i++) {
        const [_, age] = persons[i]
        if (age == minAge) {
            for (let j = 0; j < n; j++) {
                // 余りをとる
                const idx = (i + j) % n
                const name = persons[idx][0]
                log(name)
            }
        }
    }
}

let inputs = "";
let inputArray: string[];
let currentIndex = 0;

function next() {
    return inputArray[currentIndex++];
}
function nextNum() {
    return +next();
}
function nextBigInt() {
    return BigInt(next());
}
function nexts(length: number) {
    const arr = [];
    for (let i = 0; i < length; ++i) arr[i] = next();
    return arr;
}
function nextNums(length: number) {
    const arr = [];
    for (let i = 0; i < length; ++i) arr[i] = nextNum();
    return arr;
}
function nextBigInts(length: number) {
    const arr = [];
    for (let i = 0; i < length; ++i) arr[i] = nextBigInt();
    return arr;
}

// デバッグ環境がWindowsであれば条件分岐する
if (process.env.OS == "Windows_NT") {
    const stream = createInterface({
        input: process.stdin,
        output: process.stdout,
    });
    stream.on("line", (line) => {
        inputs += line;
        inputs += "\n";
    });
    stream.on("close", () => {
        inputArray = inputs.split(/\s/);
        main();
    });
} else {
    inputs = fs.readFileSync("/dev/stdin", "utf8");
    inputArray = inputs.split(/\s/);
    main();
}

B - Subscribers

B - Subscribers

整数 N が与えられ、以下の指示に従って N の近似値を出力する

• N が 10^3 - 1 以下ならば、N をそのまま出力する。

• N が 10^4 - 1 以下ならば、N の一の位を切り捨てて出力する。

• N が 10^5 - 1 以下ならば、N の十の位以下を切り捨てて出力する。

• N が 10^6 - 1 以下ならば、N の百の位以下を切り捨てて出力する。

• N が 10^7 - 1 以下ならば、N の千の位以下を切り捨てて出力する。

• N が 10^8 - 1 以下ならば、N の一万の位以下を切り捨てて出力する。

• N が 10^9 - 1 以下ならば、N の十万の位以下を切り捨てて出力する。

コンテスト中はIF文を地道に書いたが…
桁が一つ上がるにつれて、段々と切り捨てる桁も増えている。
例えば9999 みたいな数字があったとすると、答えは9990。
99999だったら99900。
一般すると10の（桁数-3）乗で切り下げで割って、またかけると答え。
9999だったら10の(4-3)乗で10で割る。
999になるので、また10をかけて9990となる。

function main() {
    const n = nextNum()
    const digit = String(n).length
    const wari = 10 ** (digit - 3)
    let ans = Math.floor(n / wari)
    log(ans * wari)
}

C - Virus

C - Virus

1,2,...,N の番号がついた N 人の人が二次元平面上いる。人 i は座標 (Xi, Yi) で表される地点にいる。人 1 はウイルスに感染している。ウイルスに感染した人からユークリッド距離が D 以内にいる人にウイルスはうつる。各 i について人 i がウイルスに感染しているか判定する、と言う問題。

まず、距離がD以内にいる人を順番に辿っていくことが要件なんだな、と考える。
距離がD以内にいる人を探索するのが厄介そうな感じがあるが、Nの制約は2000までと小さい。そのため、予め組み合わせを全探索しておけばいい。

function calcDist(a: number[], b: number[]): number {
    const [x1, y1] = a
    const [x2, y2] = b
    return Math.abs(x2 - x1) ** 2 + Math.abs(y2 - y1) ** 2

}

function main() {
    const [n, d] = nextNums(2)
    const positions: number[][] = []
    const graph: Record<number, number[]> = {}
    for (let i = 0; i < n; i++) {
        const [x, y] = nextNums(2)
        positions.push([x, y])
        // graphを初期化しておく
        graph[i] = []
    }
    for (let i = 0; i < n - 1; i++) {
        for (let j = i + 1; j < n; j++) {
            const a = positions[i]
            const b = positions[j]
            // ユークリッド距離がd以内だったらつなげる
            const dist = calcDist(a, b)
            if (dist <= d ** 2) {
                graph[i].push(j)
                graph[j].push(i)
            }
        }
    }
    const answer: String[] = new Array(n).fill('No')
    // ０から順番にたどって答えを更新
    const que: number[] = []
    que.push(0)
    const vis: Set<number> = new Set()
    vis.add(0)
    while (que.length > 0) {
        const now = que.pop()!
        answer[now] = 'Yes'
        for (const ver of graph[now]) {
            if (vis.has(ver)) continue
            vis.add(ver)
            que.push(ver)
        }
    }
    for (const ans of answer) {
        log(ans)
    }
}

D - A Piece of Cake

D - A Piece of Cake

W*HのXY平面上にある長方形のケーキにN個のイチゴが載っている。
ケーキをA本の直線でx軸に平行に切り、さらにB本の直線でy軸に平行に切ることによって、(A+1)(B+1)個のピースに分割する。そのうちの1つを選んで食べるとき、選んだピースに含まれるイチゴの個数の最小値と最大値を求める。

考えることが多くて難しいと思った。

こういう問題はまず図を描いてみる。
入力例１の場合はこんな感じ。

合計で９個に分割されたことが分かる。
ここで、答えは何もない０個が最小で、最大は２個のエリア。

これを求めることを考える。
素朴に考えると、エリアを全探索して、イチゴも全探索して、数え上げれば答えは出せそう。ただし、A,Bは10^5まであるので最大でエリアだけで10^10くらいまでなる。そのため、明らかに厳しい。

発想を転換して、イチゴが含まれるエリアを記録する、という風に考える。
左下の１点にイチゴを集中させるイメージ。

イチゴの数の最大は2 * 10^5ほど。そのため、このように転換させれば、計算量が大幅に減らせる。

次に左下に寄せる動作を行う方法について考える。
Aの配列は[2,5]
Bの配列は[3,4]
ここにそれぞれ番兵を入れて…
A:[0,2,5,W]
B:[0,3,4,H]
というようにする。

たとえば(6,2)のイチゴについて、6を超えないAの最大値、2を超えないBの最大値を求めと、(5,0)が左下の点。これは二分探索を用いれば高速に判定できる。
あとは左下の点ごとにハッシュテーブルで数を足し上げていく。
その最小と最大が答えとなる。
注意点はこの方法だとイチゴが存在しないエリアは検知できない。
逆に言うとハッシュテーブルの要素数が、エリア数に満たない場合は必ずイチゴが０個のエリアがある。

/**
 * 
 * @param arr ソート済みの配列
 * @param x 検索値
 * @returns 
 * 値 x が最初に現れるインデックスを返す。
 * x が arr 内に存在しない場合は、x を挿入するためのインデックスを返す
 */
export const bisectLeft = (arr: number[], x: number, lo: number = 0, hi: number = arr.length): number => {
    while (lo < hi) {
        const mid = Math.floor((lo + hi) / 2);
        if (arr[mid] < x) {
            lo = mid + 1;
        } else {
            hi = mid;
        }
    }
    return lo;
}

function main() {
    const [w, h] = nextNums(2)
    const n = nextNum()
    const strawberries: number[][] = []
    // イチゴの位置を記録
    for (let i = 0; i < n; i++) {
        const [x, y] = nextNums(2)
        strawberries.push([x, y])
    }
    // 0と最大値で番兵を置いて配列を作る
    const A = nextNum()
    const arrA: number[] = [0]
    const positionsA = nextNums(A)
    for (const pos of positionsA) {
        arrA.push(pos)
    }
    arrA.push(w)
    const B = nextNum()
    const arrB: number[] = [0]
    const positionsB = nextNums(B)
    for (const pos of positionsB) {
        arrB.push(pos)
    }
    arrB.push(h)
    // イチゴの数のカウンター
    const counter: Record<string, number> = {}
    // イチゴを繰り返す
    for (const strawberry of strawberries) {
        const [x, y] = strawberry
        // 二分探索でxとyを超えない最大値を検出
        const posX = bisectLeft(arrA, x) - 1
        const posY = bisectLeft(arrB, y) - 1
        // 文字列で交点を示すキーを作る
        const key = `${posX},${posY}`
        if (counter[key]) {
            counter[key]++
        } else {
            counter[key] = 1
        }
    }
    let ansMin = 10 ** 10
    let ansMax = 0
    for (const key in counter) {
        const cnt = counter[key]
        ansMin = Math.min(ansMin, cnt)
        ansMax = Math.max(ansMax, cnt)
    }
    // エリアの数は(A+1)*(B+1)
    // カウンターの要素数がこの数に満たなければ必ず０がある
    if (Object.entries(counter).length < (A + 1) * (B + 1)) ansMin = 0
    log(ansMin, ansMax)
}

E - Good Graph

E - Good Graph

N 頂点 M 辺の無向グラフ G が与えられる。
すべての i=1,2,...,K について、頂点 xi と頂点 yi を結ぶパスが存在しないとき、Gは良いグラフと呼ばれる。
Q 個の質問で与えられたグラフ G に頂点 p と頂点 q を結ぶ無向辺を追加する。新しいグラフが良いグラフであるかどうかを判定する。

まず何を言っているかよくわからない、というのが初見の感想だった。
グラフ問題はとりあえず図を描いてみることが重要。

入力例１は以下。

6 6
1 2
2 3
2 3
3 1
5 4
5 5
3
1 5
2 6
4 3
4
2 5
2 6
5 6
5 4

まずグラフ部分を図にするとこうなる。

次にKの部分について、頂点を赤線で結んでみる。

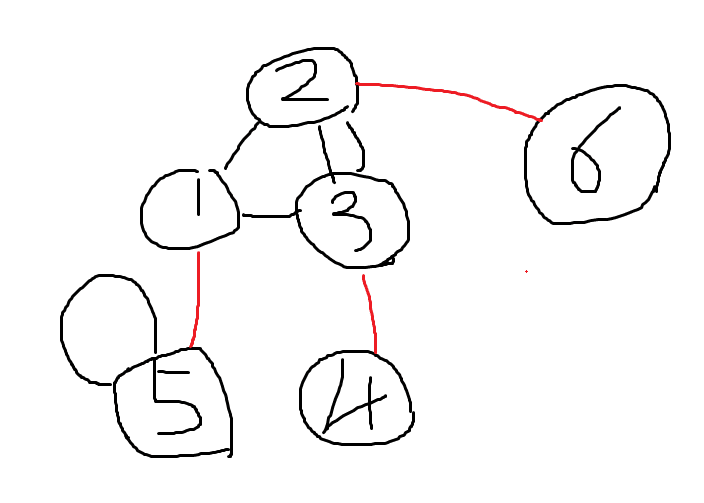
解読するのに苦労するタイプの問題だが、図に書くと見えてくる。
ある頂点とある頂点を結ぶパスが存在する、ということは、島から島へ行き来するパスが存在するイメージ。

なのでそれぞれの島ごとにくくって…

大分見通しがよくなってきた。
この赤線があるとダメなんだな、という問題であることが分かる。

つまりQ個のクエリそれぞれで結合した場合で、赤線がある島同士がつながってしまったらNG。

とりあえずそれぞれの島はUnionFindすれば求められそう。

次につないだらNGな島の組み合わせを記録しておく。
Q個の質問のそれぞれでつながることになる島を調べて、NGな組み合わせでなかったらOKという手順で問題を解く。

export class UnionFind {
    private parents: number[];

    constructor(private n: number) {
        this.parents = Array.from({ length: n }, () => -1);
    }

    public find(x: number): number {
        if (this.parents[x] < 0) {
            return x;
        } else {
            this.parents[x] = this.find(this.parents[x]);
            return this.parents[x];
        }
    }

    public union(x: number, y: number): void {
        x = this.find(x);
        y = this.find(y);

        if (x === y) {
            return;
        }

        if (this.parents[x] > this.parents[y]) {
            [x, y] = [y, x];
        }

        this.parents[x] += this.parents[y];
        this.parents[y] = x;
    }

    public size(x: number): number {
        return -this.parents[this.find(x)];
    }

    public same(x: number, y: number): boolean {
        return this.find(x) === this.find(y);
    }

    public members(x: number): number[] {
        const root = this.find(x);
        return Array.from({ length: this.n }, (_, i) => i).filter(i => this.find(i) === root);
    }

    public roots(): number[] {
        return Array.from({ length: this.n }, (_, i) => i).filter(i => this.parents[i] < 0);
    }

    public groupCount(): number {
        return this.roots().length;
    }

    public allGroupMembers(): Map<number, number[]> {
        const groupMembers = new Map<number, number[]>();
        for (let member = 0; member < this.n; member++) {
            const root = this.find(member);
            if (!groupMembers.has(root)) {
                groupMembers.set(root, []);
            }
            groupMembers.get(root)!.push(member);
        }
        return groupMembers;
    }
}

function main() {
    const [n, m] = nextNums(2)
    const uf = new UnionFind(n + 1)
    for (let i = 0; i < m; i++) {
        const [u, v] = nextNums(2)
        // つながっている頂点をunionしてgroup分けする
        uf.union(u, v)
    }
    const k = nextNum()
    // NGになる組み合わせ
    const badPair: Record<number, Set<number>> = {}
    // 初期化しておく
    for (let ver = 1; ver < n + 1; ver++) {
        badPair[ver] = new Set()
    }
    for (let i = 0; i < k; i++) {
        const [u, v] = nextNums(2)
        // NGな島のrootを記録
        const uRoot = uf.find(u)
        const vRoot = uf.find(v)
        badPair[uRoot].add(vRoot)
        badPair[vRoot].add(uRoot)
    }
    const query = nextNum()
    for (let i = 0; i < query; i++) {
        const [p, q] = nextNums(2)
        // つなぐ島のrootを求める
        const pRoot = uf.find(p)
        const qRoot = uf.find(q)
        // NG組み合わせにあったらNo
        if (badPair[pRoot].has(qRoot) || badPair[qRoot].has(pRoot)) {
            log('No')
        } else {
            log('Yes')
        }
    }
}

おわりに

unratedになってしまったのは率直にいって残念だった。個人的には好きなアルゴリズムのUnionFindを使うことでE問題まで到達できたので、その点には満足している。AtCoder社には引き続き運営を頑張ってもらいたい。ではでは。