
AtCoder精選良問「D - Takahashi Tour」Diff 710
この記事はAtCoderの精選良問集マガジンの中の記事です。
私が良問だと思った問題を解説付きでまとめています。
問題リンク
問題概要
DFSを履修するのに最適な問題。
AtCoder 国には 1 から N の番号がついた N 個の都市が存在する。
また、1 から N−1 の番号がついた N−1 個の道路があり、道路 i を通ると都市 Ai と都市 Bi の間を相互に移動できる。
すべての都市は道路を使って互いに行き来できることが保証されている。
このような問題設定の中、以下のルールで移動を繰り返す。
都市 1 から出発する。
現在いる都市と直接つながっている未訪問の都市がある場合、その中で最も番号の小さい都市へ移動する。
未訪問の都市が存在しない場合、以下の場合に分かれる。
現在いる都市が都市 1 である場合、旅を終了する。
現在いる都市が都市 1 でない場合、最後に訪れた都市へ戻る。
すべての都市を訪問するまで 2 から 3 を繰り返す。
このようなルールで移動を繰り返し、訪問した都市を順に出力する、というのがこの問題の概要。
考え方
このように都市がつながっているという問題の場合は、まずグラフ探索を考える。
グラフ探索と言えばBFS(幅優先探索)かDFS(深さ優先探索)を使うことが多いのだけど、この問題ではDFSの方を使う。
なぜそうなのかの言語化をしてみる。
幅優先探索は一言で言うと、開始頂点から距離が近いところを順につぶしていく、つまり「今いるところから近いところを順番につぶしていこうぜ」というような探索アルゴリズム。
対して深さ優先探索。こちらは距離の近さは関係なく、猪突猛進的に進む。つまり、「行けるところまで行って、駄目だったら戻ろうぜ」というように頂点を探索するアルゴリズム。
例えば以下のようなグラフを考えてみる。
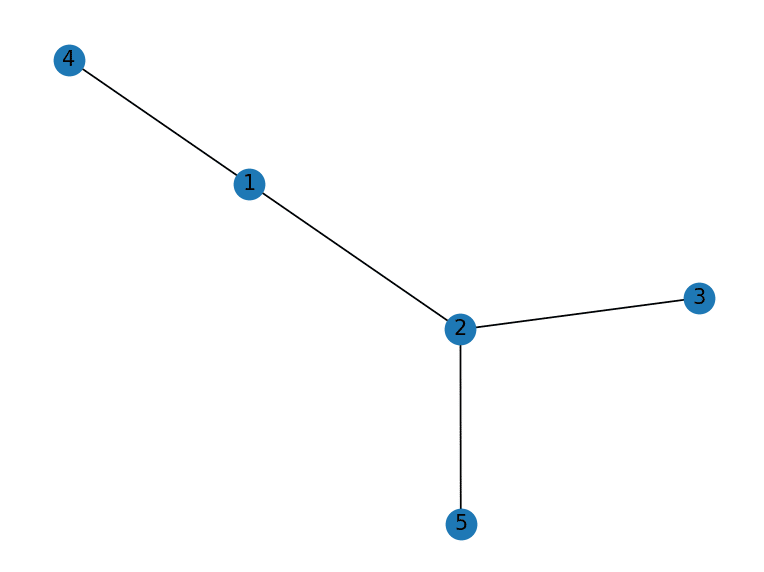
幅優先探索の場合は頂点1から始めて、近いところを攻めていく。
この場合だと2と4を次に探索する場所としてつぶす。
4から行ける場所はないので、そこから先は探索しない。
2から3と5にいけるので、また探索する、というような感じ。
対して深さ優先探索の場合は、とりあえず2か4のどちらかに猪突猛進的に進む。
例えば先に4に行った場合はそれ以上先に行けないので、また1に戻ってくる。次に2に行く。3か5のどちらかに行く、というようなイメージ。
どちらも全部を探索するのだが、探索する順番が異なる。
この問題が「都市1から始めて近い距離の都市を出力する」だったら幅優先探索が有効だ。しかし、そうではなくて、「戻った行程も含めて経路を出力する」という問題設定なので、深さ優先探索を使って実装を行っていく。
深さ優先探索というと、再帰関数を使った実装が多い。
だが、自分はstackを使って書くことが多い。
なぜなら再帰は慣れていなくて自分には難しいからだ。
関数が関数自身を呼び出すということを考えると頭がこんがらがってくる。
よくわからなくなってきて、「サイキ」という単語が頭の中を占めてくる。
そうしているうちに、Buffalo Daughterの「Pshychic A-Go-Go」が脳内で再生される。名曲だ。最早問題のことはどうでもよくなってしまう。
暇な人はこれを機に聴いてみてほしい。
さて、話を戻そう。DFSは適切に組むことでstackを使って実装できる。
基本的な方針としては次の頂点をstackに加える前に、今いる頂点を-1でかけたものを加えておくようにする。上の1から4に行く場合は、以下のようにstackに加える。
stack=[]
stack.push(-1)
stack.push(4)stackではpop()して取り出していくので、4から先に行ける場所はないので、次に-1が取り出される。マイナスの数字になった場合は戻ってきた場合をあらわすので、反転させて記録していけばいい。この辺りは実コードを見た方がイメージがつくと思う。
実装
「いったことのない都市のうち、一番小さいところに行く」というルールがあるので、グラフデータを構築した後に、大きい順にsort()をするのがこの問題の肝となる部分。
こうすること小さい順にstackから取り出せるので、問題の要件を満たせる。
import { createInterface } from "readline";
import * as fs from "fs";
import { log } from "console";
function main() {
const n = nextNum()
const graph: Record<number, number[]> = {}
// graphを構築
for (let i = 0; i < n - 1; i++) {
const [a, b] = nextNums(2)
if (graph[a]) {
graph[a].push(b)
} else {
graph[a] = [b]
}
if (graph[b]) {
graph[b].push(a)
} else {
graph[b] = [a]
}
}
// graphをsortして大きい順に並べる。
for (let i = 1; i < n + 1; i++) {
graph[i].sort((a, b) => b - a)
}
// 答えの配列
const ans: number[] = []
// 訪れた都市を記録
const vis: Set<number> = new Set()
vis.add(1)
const stack: number[] = [1]
while (stack.length > 0) {
const nowCity = stack.pop()!
if (nowCity > 0) {
// 答えに記録
ans.push(nowCity)
const adjCities = graph[nowCity]
for (const city of adjCities) {
// 既に訪れている場合は加えない
if (vis.has(city)) continue
// 今いる都市をマイナスして加える
stack.push(-1 * nowCity)
// 次の都市を加える
stack.push(city)
// visに加える
vis.add(city)
}
} else {
// nowCityがマイナスということは先に行けなくなってnowCityに戻ってきた
// -1をかけて答えに加える
ans.push(-1 * nowCity)
}
}
log(ans.join(' '))
}
let inputs = "";
let inputArray: string[];
let currentIndex = 0;
function next() {
return inputArray[currentIndex++];
}
function nextNum() {
return +next();
}
function nextBigInt() {
return BigInt(next());
}
function nexts(length: number) {
const arr = [];
for (let i = 0; i < length; ++i) arr[i] = next();
return arr;
}
function nextNums(length: number) {
const arr = [];
for (let i = 0; i < length; ++i) arr[i] = nextNum();
return arr;
}
function nextBigInts(length: number) {
const arr = [];
for (let i = 0; i < length; ++i) arr[i] = nextBigInt();
return arr;
}
// デバッグ環境がWindowsであれば条件分岐する
if (process.env.OS == "Windows_NT") {
const stream = createInterface({
input: process.stdin,
output: process.stdout,
});
stream.on("line", (line) => {
inputs += line;
inputs += "\n";
});
stream.on("close", () => {
inputArray = inputs.split(/\s/);
main();
});
} else {
inputs = fs.readFileSync("/dev/stdin", "utf8");
inputArray = inputs.split(/\s/);
main();
}オイラーツアーを使う
ちなみにこの問題はオイラーツアーと呼ばれる典型的なアルゴリズムを使って解くことができる。
オイラーツアーとは、深さ優先探索を使って以下の配列を返すようなアルゴリズム。
訪問した頂点の順序
各頂点の最初の訪問時刻
各頂点の最後の訪問時刻
典型的に使えそうなアルゴリズムは関数化しておくと、同じような問題にあたったときによい。以下のようになる。
type Graph = { [key: number]: number[] };
export const eulerTour = (n: number, graph: Graph, root: number): [number[], number[], number[]] => {
const parent: number[] = Array(n).fill(-1);
const stack: number[] = [~root, root];
let currTime: number = -1;
const tour: number[] = [];
const inTime: number[] = Array(n).fill(-1);
const outTime: number[] = Array(n).fill(-1);
while (stack.length > 0) {
const currNode: number = stack.pop() as number;
currTime += 1;
if (currNode >= 0) {
tour.push(currNode);
if (inTime[currNode] === -1) {
inTime[currNode] = currTime;
}
for (const nextNode of graph[currNode]) {
if (nextNode !== parent[currNode]) {
parent[nextNode] = currNode;
stack.push(~nextNode);
stack.push(nextNode);
}
}
} else {
outTime[~currNode] = currTime;
if (parent[~currNode] !== -1) {
tour.push(parent[~currNode]);
}
}
}
return [tour, inTime, outTime];
}一見して先ほどの問題を解いたコードと同じような感じの実装。
異なる点は直前に訪れたnodeをparentで管理している。そして、stackに加える時にstack.push(~nextNode)してtourを構築するようにしている。
これをそのまま使えば答えになる。
function main() {
const n = nextNum()
const graph: Record<number, number[]> = {}
// graphを構築
for (let i = 0; i < n - 1; i++) {
const [a, b] = nextNums(2)
if (graph[a]) {
graph[a].push(b)
} else {
graph[a] = [b]
}
if (graph[b]) {
graph[b].push(a)
} else {
graph[b] = [a]
}
}
// graphをsortして大きい順に並べる。
for (let i = 1; i < n + 1; i++) {
graph[i].sort((a, b) => b - a)
}
const [tour, inTime, outTime] = eulerTour(n + 1, graph, 1)
log(tour.join(' '))
}この記事が気に入ったらサポートをしてみませんか?
