「KAN: Kolmogorov-Arnold Networks」の要約

概要

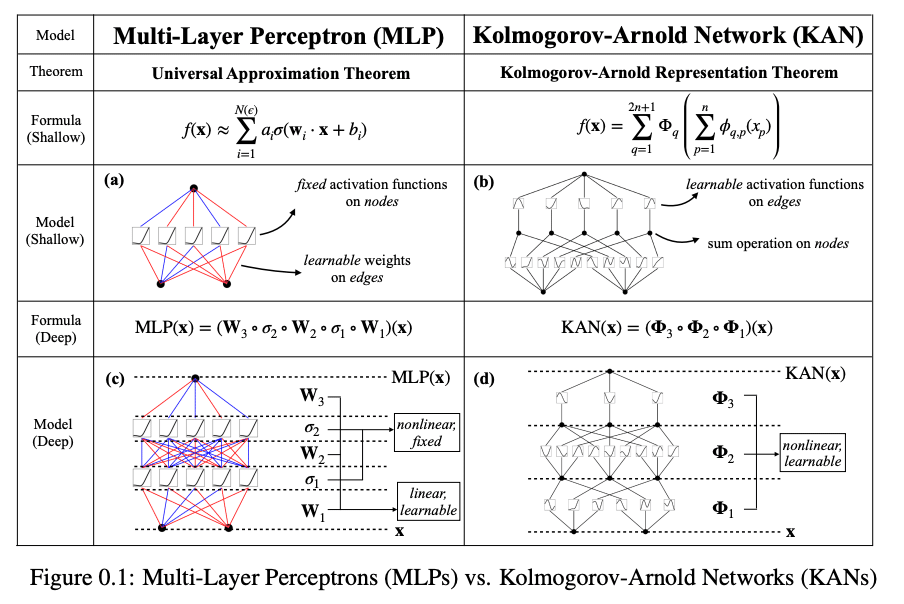
　KAN（Kolmogorov-Arnold Networks）は、多層パーセプトロン（MLP）に代わる有望な選択肢として提案されています。MLPがノードに固定された活性化関数を持つのに対し、KANはエッジに学習可能な活性化関数を持ちます。KANは線形重みを持たず、その代わりに各重みがスプラインとしてパラメータ化された一変数関数に置き換えられています。このシンプルな変更により、KANは精度と解釈性の面でMLPを上回ります。

KANとMLPの違い

MLPについて

　MLP（多層パーセプトロン）は、基本的なニューラルネットワークの構造です。これは、入力層と出力層の間に複数の隠れ層を持つ構造で、各ノード（ニューロン）が入力からの線形変換を行い、その結果に固定された活性化関数を適用して出力します。この活性化関数は、一般的にはシグモイド関数やReLUなどが使われ、ノードに固定されています。

KANについて

　KAN（Kolmogorov-Arnold Networks）は、MLPに似た構造を持ちますが、MLPの弱点を補うために重要な違いがあります。

• 活性化関数の配置: MLPでは活性化関数はノードごとに固定されていましたが、KANではこれがエッジ（ノード間の接続）に配置され、その関数が学習可能となっています。つまり、KANでは各エッジにおける活性化関数の形状がデータに合わせて変化することができるのです。

• スプライン関数: KANでは線形重みがなく、代わりに各エッジにおいてスプラインという一変数関数が使われます。スプラインは曲線を滑らかに繋げるための関数で、その形状は複数の点（グリッドポイント）によって定義されます。このグリッドポイントの位置やスプラインの係数は学習によって調整され、最適な形に変化します。

精度

　KANの活性化関数はエッジに置かれており、それぞれがスプラインとして学習できるため、より柔軟で精度の高いモデルが作れます。結果として、同等またはより少ないパラメータ数で、MLPよりも高い精度を達成することができます。

解釈性

　KANの構造はノード間の接続がどのような関数で表現されているかが見えるため、MLPよりも直感的に理解しやすくなっています。また、KANは特定の関数を持つデータセットに対して、比較的簡単にその関数に近い形に収束する傾向があり、その点でも解釈しやすくなっています。

実践

　KANの実装では、深さや幅の任意のバリエーションを持つKANを設計し、バックプロパゲーションを用いてこれをトレーニングできます。KANはMLPと比較して有意にスケーリング法則が良いことが示されています。

結論

　KAN（Kolmogorov-Arnold Networks）は、MLP（多層パーセプトロン）に代わる有望な選択肢として提案されています。KANはKolmogorov-Arnold Representation Theoremに基づき、エッジに学習可能なスプライン関数を使用することで、高い精度と解釈性を提供します。これにより、データフィッティングやPDEソルビングにおいてMLPよりも効率的であり、科学や数学の法則を示す際にも直感的に理解しやすいという特長があります。KANは深層学習の分野でのさらなる発展に寄与し、幅広い応用が期待されます。

https://arxiv.org/abs/2404.19756