過去データから将来を予測する 2 (ARCH,GARCHモデル、ベイジアン他)

前回に引き続き、今回はARCHモデル、GARCHモデル、Interpolation、ベイジアン予測といった手法を見ていく。

前回は以下参照。（分析の前提条件も記載してあるので、まだの方は是非）

---

分散自己回帰(ARCH)モデル

AutoRegressive Conditional Heteroscedasticity models

分散不均一性を示す時系列データに適用されるモデルで、分散自己回帰モデルや分散不均一モデルと呼ばれる。金融時系列データへの適用事例が多い。

このモデルでは、線形モデルであるARモデル（係数を特定し、公式を作り、それを時系列データに当てはめた際の残差がホワイトノイズであれば、信頼性は高いとするモデル）には当てはまらない。
実際に為替レートや株価などの金融商品の時系列データの残差の分散は一様ではなくばらつきに特徴がある、

つまり、
「分散の不均一性（heteroscedasticity）」があるものを分析するのに使用する。ARCHモデルでは、今期の分散が過去の分散に依存することをモデルに組み入れる。

*Heteroscedasticity: 分散が一定でないこと
*Homoscedasticity: 分散が一定であること

ARCH(q)モデルの定義式は、

σt^2 = α1(ε_(t-1))^2 + α2(ε_(t-2))^2 +...+ αq(ε_(t-q))^2  (*)
εt = σt N(0,1)

*εt: 誤差

上記の定義式を使ったロバート・エンゲル (1982) が提案した ARCH(q) モデルは以下の通りである。

1. 最も適合する自己回帰モデルAR(q)を推定する
（但し、y_tは単位根を持たない）

2. 誤差εtの二乗を求め、定数とq個のラグ値で回帰する。

ここで、qはARCHラグの長さとなる。

※一応数式を書きましたが、考え方が分かればOK。

一般化分散自己回帰(GARCH)モデル

Generalized AutoRegressive Conditional Heteroscedasticity models

一般化されたARCH である GARCH(p,q)モデルは次のような形で与えられる。

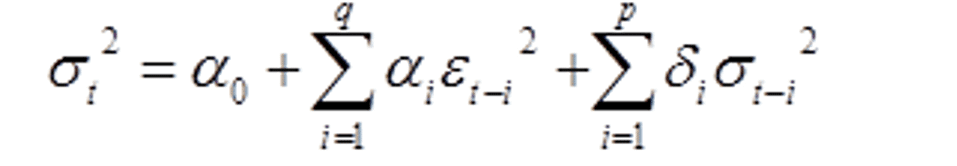
ここで、定数αとδはヒストリカル回帰で求め、εはARCHモデルの時と同様に求める。

内挿 (Interpolation)

非常に数学的な概念で多くの場合、状態空間に入って、組み合わせのルールを定義するもの。

一見難しそうに聞こえるが、例えば、
金利（IR）、雇用率（ER）、個人消費（CS）を使ってGDPの数値を予測する場合、すでに観測された金利、雇用率、個人消費の値をいくつか組み合わせて現在の経済状態がどうなっているかを判断し、それに対応するGDPを導き出すことができるという単純な手法。

例：以下のデータが観察されたとする。
(ir1,er1,cs1,gdp1) = (0.05, 0.96, 3×10^10,7×10^10),
(ir2, er2, cs2, gdp2) = (0.06, 0.89, 4×10^10,6×10^10),

そして、現在の状態は (IR3,ER3,CS3) = (0.055, 0.925, 35×10^9)である。

データから、
(IR3,ER3,CS3)=0.5*((IR1,ER1,CS1)+(IR2,ER2,CS2))
という数式（0.5という係数）が導き出せるので、

GDPは 0.5*(7+6)×10^10 =6.5×10^10
になると結論づけることができる。

もちろん、これは非常に単純化されたモデルであり、多次元での補間のルールは慎重に定義する必要がある。

内挿関係を定義すると、
GDP = f(IR, ER, CS, a1 and a2) --- fは推測される
ここで、fは2つのパラメータa1、a2に依存する所定の（経験的に推測される）関数である。
パラメータの数は、通常、観測点の数に依存する。

ベイジアン予測

このモデルには線形モデルと非線形モデルがあり、少し複雑ではあるものの、回帰と似ている。

ダイナミックベイズモデル

逐次的なアプローチであり、ランダムな観測はパラメータ、例えば時間tでラベル付けされる。
F(Yt | θt, D_(t-1))

F: 時刻tにおける変数Yの確率分布
θ: 時刻tで決定されるパラメータのセット
D: t-1における既知情報のセット。

θの典型的な例は、回帰パラメータ、季節要因、または期待値や標準偏差のような他の定量的情報。

標準ダイナミック線形モデル (Normal dynamic linear models)

Yt = Ft' θt + vt
θt = Gt θ_(t-1) + ωt

θt: 時刻tにおける状態ベクトルであり、通常は経験則から判明する。
Ft: 既知の定数ベクトル（回帰、滑らかな傾向、時間変化する季節的/周期的挙動、伝達応答などの方法を用いたバックデータフィッティングから得られる）。
vt: 平均値ゼロ、分散既知のノイズで、通常は正規分布。
Gt: 状態進化行列で，ほとんどの場合，恒等式とすることができる．
ωt: 平均0、共分散行列tが既知の進化ノイズで、通常N(ωt | 0, W𝑡)となる。

---

ChatGPTが最近すごい話題になっていて、先日OpenAIのCEOが総理大臣と対談して日本拠点を作るだとか言ってるみたいですね。。

論文の要点をパッパと読みたくて、Twitterで話題になっていたChatGPTに論文を読ませて要約する命令文を使ってやってみたら、結果は散々でした。
回答は的を得ておらず、平気で嘘ついたりする。
ということで、素直にAbstractを読むのが一番早いという結果でした。

まだまだ僕らの仕事を奪いに来るレベルまで遠そうだ。