人気講師ノート16_吸光度分析を考えるうえで必要な軌道の話

さて，前回までの記事でLambert-Beerの法則をおさらいしつつ，突っ込んだお話も書かせていただきました。
▼
同じ赤色でも【透明】と【不透明】があること。

不思議に思いませんか？

なぜ，ルビーの赤は【透明】であって，赤サンゴの赤は【不透明】なのでしょうか？原料が違うから！！まー、そうなんですが，，このあたりを電子，軌道，結合を理解したうえで，透明と不透明を説明できた方がかっこいいですよ。　

復習もかねて，下記の記事を貼っておきますね。
人気講師ノート12　吸光光度分析と蛍光光度分析
人気講師ノート13　ランバートベールの法則について_溶媒とセルもね
人気講師ノート14　ランバートベールの法則から導かれる吸光度の最適値
人気講師ノート15　ランバートベールの法則の適用限界について

▼

いよいよ，吸光光度分析について～～～と思うのですが，

その前に！

原子軌道とその結合(σ，π)の話です。

軌道については，こちらの説明が視覚的にもわかりやすいと思いますので，詳しくはこちらをご覧ください。

さて，ざっくり原子軌道のお話として，それぞれの形から得られる情報です。原子軌道の形は統計的な確率的なものであり，波動性と粒子性があり，なんてのはここでは書かずに，また別の機会に書きたいと思います。

1.　ボーアの原子構造論

おそらく，中高で学ぶボーアの原子構造論(ボーアの原子半径)を思い出されるかと思います。月が地球の周りをまわっているように，電子も原子核の周りをクルクル回っているイメージが根深いかと思います。

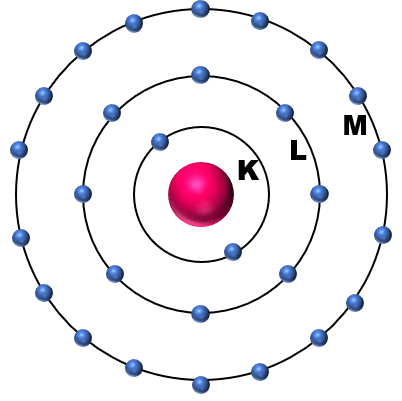
もう少し学びますと，ボーアの原子構造を形成している殻(K殻，L殻・・・)には，さらに【軌道；orbital function】というものがあることを知ります。そして，電子の動きは円だけではなく，もっといろいろな形があることを知ります。(正確には，原子核に対して電子が存在する位置の確率(密度分布)のことを軌道として学びます。)

2-1.　原子軌道について

それらの動く形(原子軌道)を，単純な形から【s軌道】，【p軌道】，【d軌道】，【f軌道】なんて言ったりします。シュレーディンガー方程式を説明したいのはやまやまなのですが，他の方の記事にお願いしたいと思います。

下記に図を示したように，s軌道は1種類の球形，p軌道は3種類の亜鈴形，d軌道は5種類の形があります。この各軌道の種類の違いについても，量子化学ノートでおいおい説明していきたいと思いますが、とりあえず申し訳ありません。パスです。

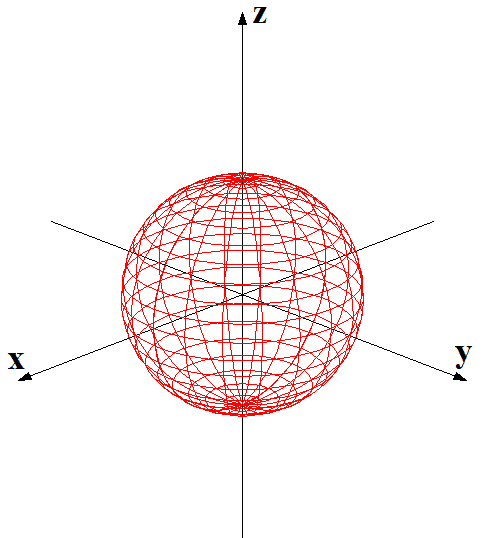
この赤と青は反対の性質を持っているということです。単独ではあまり意味を持たずに、結合する際には意味が出てきます。
教科書には，プラスやマイナスが表記されていますが，電荷のプラスマイナスではなく，反対の性質，あるいは電子の存在確率，つまり赤い部分に電子がいるときには，青い部分には電子が存在する可能性が低く，赤い部分に電子がいない場合は，青い部分には電子がいる可能性が多いといった意味が伝わりやすいでしょうか。。

それぞれの軌道には名称がついています。p軌道は3種類あって，x軸上に拡がっている軌道がpx軌道，y軸に拡がっている軌道はpy軌道と呼びます。
d軌道は，5種類あって，z軸上に拡がっている軌道はdz^2（ｄz2乗），x軸とy軸上に拡がっている軌道はdx2-y2（dx2乗ーy2乗）と呼びます。xy平面に軌道が広がっているのがdxyです。軸上か平面上かの違いがあります。

2-2.分子軌道について

さて，これらの原子軌道が結合することで分子軌道が考えられます。ルールとしては，

N個の原子軌道から，N個の分子軌道が形成される

x軸上に，2個の原子があって，それらがx軸上で互い近づいて分子軌道を形成するときのことを考えてみましょう。

2-2a. s軌道による分子軌道について

結合性軌道であるσ(シグマ)軌道と反結合性軌道であるσ*(シグマスター)軌道ができる。エネルギー差を示したように，結合性軌道の方がエネルギーが低く安定であるといえる。この分子軌道形成による安定化が，原子単独でいるより分子となったほうが有利であることを示しているが，これも別の機会に

また，形成された分子軌道の「中心反転」を考えて，同じ色のものをゲラーデ(Gerade=偶関数)，違う色のものをウンデラーデ(Ungerade＝奇関数)と呼び，それぞれぼσの後に，「g」や「u」を併記する。

また，結合軸(この場合，X軸)に沿って，回転対称となるものを【対称な軌道】と呼び，回転対称とならないものを【逆対象な軌道】と呼ぶ。

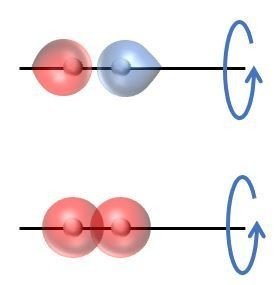
2個のs軌道から，1個の結合性軌道と1個の反結合性軌道の2個の分子軌道が形成される。
●結合性軌道はσ軌道であり，ゲラーデであり，対称な軌道である。
●反結合性軌道はσ*軌道であり，ウンゲラーデであり，対称な軌道である。

これを踏まえて，p軌道同士の分子軌道についても考えてみよう。

2-2b. p軌道による分子軌道

x軸上に沿って結合することを，原子軌道の空間分布が異なるために，重なりに違いが出ます。
まずは，x軸上に軌道の広がりがあるpx軌道同士の分子軌道を考えてみる。

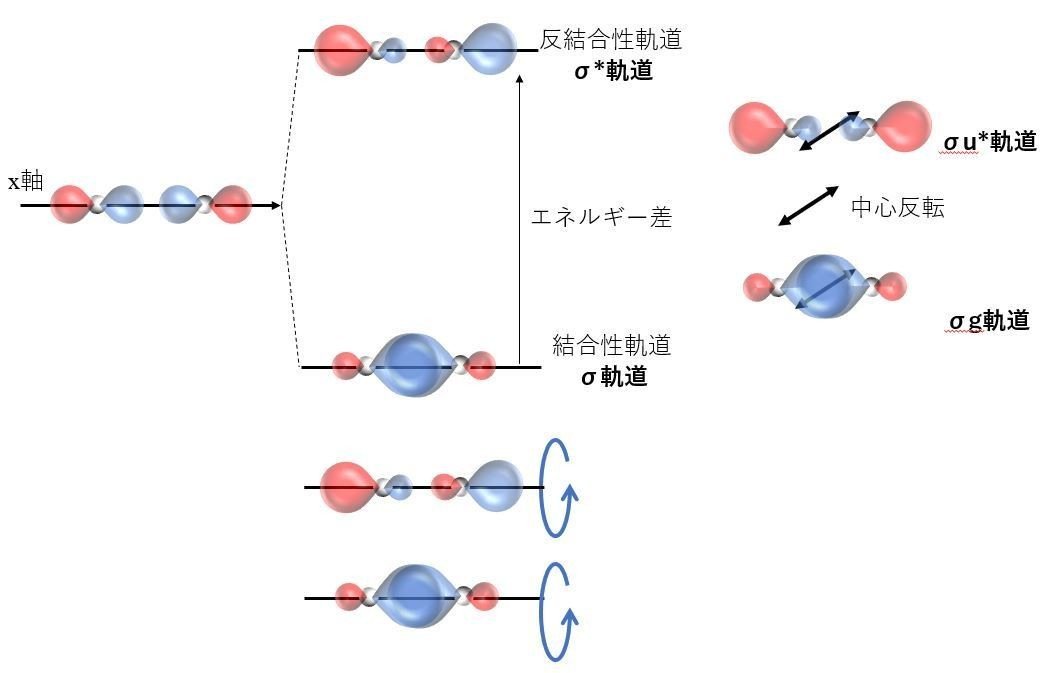
上述のs軌道の球とp軌道の亜鈴形で軌道の形は違うものの，その結合性軌道のσ結合やゲラーデや対称な軌道であることに違いはない。

つまりは，分子軌道であるσ軌道とσ*軌道は，軌道の種類によらず以下が成立することがわかる。

●σ軌道：結合性軌道，ゲラーデであり，対称な軌道
●σ*軌道：反結合性軌道，ウンゲラーデであり，対称な軌道

続いて，x軸に対して垂直なy軸とz軸に軌道の広がりがあるふたつのpy軌道同士とふたつのpz軌道同士の分子軌道の形成について考える。

先ほどのpx軌道同士(x軸に沿って結合を考慮)の分子軌道に比べて，結合性軌道と反結合性軌道の重なりが小さいために，エネルギーの安定化と不安定化はσ結合に比べ小さく，これらの分子軌道を「π軌道(結合性軌道)」と「π*軌道(反結合性軌道)」と呼ぶ。

結合性軌道であるπ軌道の【中心反転】を考えると，”σ軌道”とは違い，赤と青が入れ替わるために，結合性軌道であるπ軌道がウンゲラーデです。反結合性軌道であるπ*結合がゲラーデとなる。

また，結合軸であるx軸を回転させると，π軌道もπ*軌道も青と赤の軌道がコロコロと入れ替わることがわかるだろう。つまり，π軌道もπ*軌道も逆対称な軌道といえる。

これらのπおよびπ*軌道について，σ結合と同様なまとめをすると以下のとおりである。

●π軌道：結合性軌道，ウンゲラーデであり，逆対称な軌道
●π*軌道：反結合性軌道，ゲラーデであり，逆対称な軌道

(●σ軌道：結合性軌道，ゲラーデであり，対称な軌道)
(●σ*軌道：反結合性軌道，ウンゲラーデであり，対称な軌道)

そして，結合に関与しない結合，no-bonding orbitalであるn軌道なるものがある。分子を形成する際に結合に関与しないために，分子形成後もエネルギー的に安定も不安定化もしないとする。

2-3.　電子準位における選択則(許容と禁制)について

やっと，吸光度分析に戻れる。これまでの原子軌道や分子軌道については，だいぶ荒っぽく記述してきた。見返して，順次修正を加えていきたいが，重要なことは以下の事である。

●σ軌道：結合性軌道，ゲラーデ(偶関数)であり，対称な軌道
●σ*軌道：反結合性軌道，ウンゲラーデ(奇関数)であり，対称な軌道
●π軌道：結合性軌道，ウンゲラーデ(奇関数)であり，逆対称な軌道
●π*軌道：反結合性軌道，ゲラーデ(偶関数)であり，逆対称な軌道

そして，吸収スペクトルで観測されるのは，各分子軌道間の遷移(と緩和)で考えることができる。軌道間の遷移には，選択則(Selection Rule)が適用される。ざっくりいうと，二つのルールがあり，このルールに沿って，遷移が起こりやすい許容遷移と遷移が起こりづらい禁制遷移があることがわかる。

遷移則(Selection rules)
１．偶関数と奇関数の遷移は許容。偶関数同士および奇関数同士は禁制。
２．対称な軌道と対称な軌道，逆対称な軌道と逆対称な軌道が許容。対称な軌道と逆対称な軌道は禁制。

である。おいおい，述べていきたいのではあるが，今回はざっくり補足１と２を書いておく。

＊＊＊補足＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊
補足１：軌道A＞軌道Bへの遷移モーメントmABは，双極子モーメントuを含む次式で与えられる。

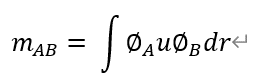
双極子モーメントuは，反転対称(原点対象)に対して奇関数であるから，∅_A ∅_Bも奇関数である必要がある。遷移モーメントがゼロになる(禁制遷移)。電子はスピンをもつ(双極子モーメントがある)＞大きさと向きがあるベクトル場と考えられる。これを原点対称の操作を行うと，-1が付くので，奇関数である。
補足２：スピン状態が不変な遷移が許容である。遷移することで，スピンがアップスピンからダウンスピンに変化するのは禁制である。これは，対称から逆対称の変化を禁制と考える。
＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

先ほどの分子軌道をざっくりとまとめると下記のような関係となる。

上記の選択則と軌道間の差(差が大きいほどエネルギーが大きい)を考慮すると，分子軌道間で起こりうる遷移はエネルギーが大きい順番から

σ　→　σ＊　遷移

続いて，

ｎ　→　σ＊　遷移

π　→　π＊　遷移

そして，

ｎ　→　π＊　遷移

となる。紫外可視吸収スペクトルにおいては，π→π＊遷移とｎ→π＊遷移が分析対象となりうる。

▼
さて，他の遷移である【σ→π＊遷移】や【π→σ＊遷移】は考慮しなくても良いのだろうか？？

選択則を考慮すると，【σ→π＊遷移】は偶関数からの偶関数の禁制遷移であり，さらには対称な軌道からの逆対称な軌道への禁制遷移である。
【π→σ＊遷移】も同様にふたつの選択則のルールの両方において禁制遷移である。つまりは，これらのふたつの遷移は選択則にのっとって，限りなく起きにくい遷移であることがわかる。

▼
今後議論対象となる紫外可視吸収スペクトルにおいては，π→π＊遷移とｎ→π＊遷移が分析対象はどうであろうか？

π→π＊遷移は，奇関数からの偶関数の許容遷移であり，逆対称な軌道間の遷移であるために，許容遷移である。

一方で，ｎ→π＊遷移は，非共有電子対が関与し，構造的に電子スピンの方向が変わることが考えられるために，実は禁制遷移である。

この許容遷移であるπ→π＊遷移と禁制遷移であるｎ→π＊遷移から，吸収スペクトルの縦軸(吸光度)に大きな差が生じる。電子遷移が起きやすいπ→π＊遷移のモル吸光係数(εmax)は大きく，電子遷移が起きにくいｎ→π＊遷移のモル吸光係数は小さい。

大げさに違いを示すと以下のような図となりうる。

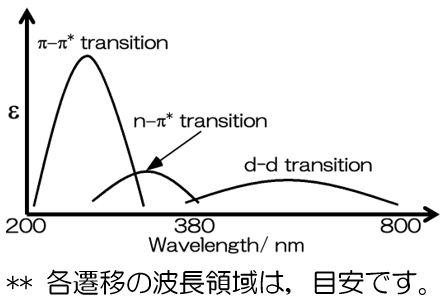
つまりは，

縦軸の吸収が大きいものは，π―π*遷移であり，小さいものはｎ→π＊遷移と推察できるということである。

本文は以上です。d-d遷移や吸収スペクトルについては，次に回します。
今回は，機器分析から逸脱している内容が多く書かれており，それを踏まえて文章を書くと，だいぶ明後日の方向に行ってしまいそうなので，詳しく正確な説明については別の機会を設けたいと思います。

まとめとしては，有機分子や金属錯体において議論対象となる遷移は，

π―π*遷移，ｎ→π＊遷移，d-d遷移である。

これらの許容遷移および禁制遷移が，ルビーとサンゴの同じ赤であるのに，透明と不透明がある理由につながるのである。