人気講師ノート14　ランベルト・ベール法則から導かれる吸光度の最適値

さて、お久しぶりです。時節柄、いろいろと予定が変わりそれの対応でなかなか資料作成ができませんでしたが、授業の遠隔授業の最適化も進める意味で様々な資料を作成しています。

今回は、前回に引き続き、ランベルト・ベールの法則に関するNoteです。

YouTubeも始めました。ご笑覧ください。

ランベルト・ベール(Lambert－Beer)の法則

A=εcl
(A：吸光度,　ε：モル吸光係数、ｃ：モル濃度、l：セルの長さ)

モル吸光係数は物質がどれくらいの光を吸収するかの定数です。
モル吸光係数とセル長は定数とも考えることができます。セル長とは、測定対象物を入れる測定容器(セル)の事です。大体、１ｃｍのものを使用します。

つまり、ランベルト・ベールの法則を用いて、物質の【モル濃度】と【吸光度】に比例関係があることがわかります。

この吸光度Aに最適値があることをご存じでしょうか？

最大で1.0であり、最適値は0.3ぐらいと言われています。この吸光度の最適値を理解するために、ランベルト・ベールの法則を導出しましょう。

ランベルト・ベール(Lambert－Beer)の法則の導出

溶液を入れた測定セルに所望の光を当てて、入射光に対する透過光で測定対象物の吸光度を測定します。

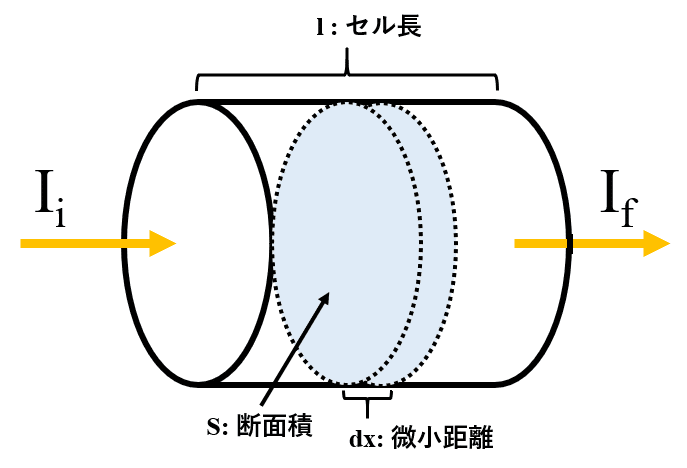
光が通過する微小体積(=断面積×微小距離；Sdx)に含まれる測定対象物の分子数は、アボガドロ数NAとモル濃度ｃから、式①が導かれます。

NA×ｃ×Sdx　・・・①

ここで、【測定対象物は独立に光を吸収】すると仮定して、測定対象物の吸収断面積(σ)を考慮して、式①から式②が導かれます。

σ×NA×ｃ×Sdx　・・・②

吸光度の最適値を考慮する上で，この【独立して光を吸収】が重要な仮定となります。以下の図からも、独立して光を吸収することで、測定対象物の吸光度が測定できることがわかります。

単位断面積Sあたり、光が測定対象物に吸収される割合は、式②から式③が導かれます。

(σ×NA×ｃ×Sdx)/S = σ×NA×ｃ×dx　・・・③

微小距離dxを進む間の光強度の減少量（-ｄI）は、入射光の強度 I(in) と単位面積あたりの光の吸収割合(式③)に比例するので、式④が導かれます。

-ｄI = I(in) × σ×NA×ｃ×dx 　・・・④

式④を少し変形して、式⑤を導きます。

―ｄI/(I(in)) = σ×NA×ｃ×dx　・・・⑤

微小距離ｘ＝０の時、入射光　I(i)　とする。微小距離ｘ＝ｌ(エル)の時、透過光　I(f) とする。式⑤を上記の範囲で積分すると以下のようになります。

ランベルト・ベールの法則(式⑥)が導けました。吸光度Aが、濃度ｃに比例しています。モル吸光係数は、吸収断面積(σ)とアボガドロ数(NA)との積である定数ともわかります。

では、吸光度Aは1.0が最大で、0.3ぐらいが最適値であることの説明

ランベルト・ベール(Lambert－Beer)の法則の導出過程において、【測定対象物は独立に光を吸収】すると仮定していたことを覚えていますでしょうか。この仮定を満たすことで、この法則は成立します。

※Case１※吸光度Aが１．０の場合を、ランベルト・ベール(Lambert－Beer)の式に代入してみます。

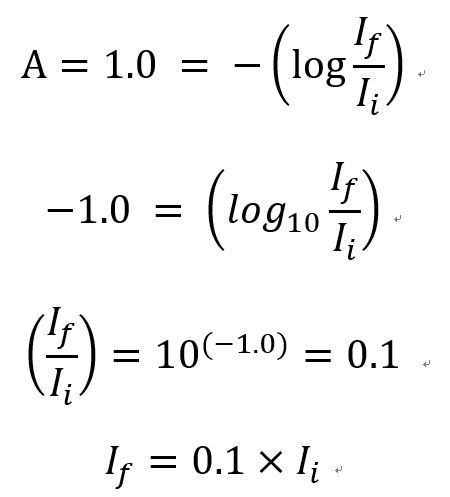
この式から、吸光度Aが１．０の場合、入射光 I(i) の0.1倍が透過光 I(f) の値と算出されます。
つまり、入射光の90％が吸収されて、入射光の10％程度が透過光として検出されることがわかります。さて、【測定対象物は独立に光を吸収】でお見せした図をもう一度見てみましょう。

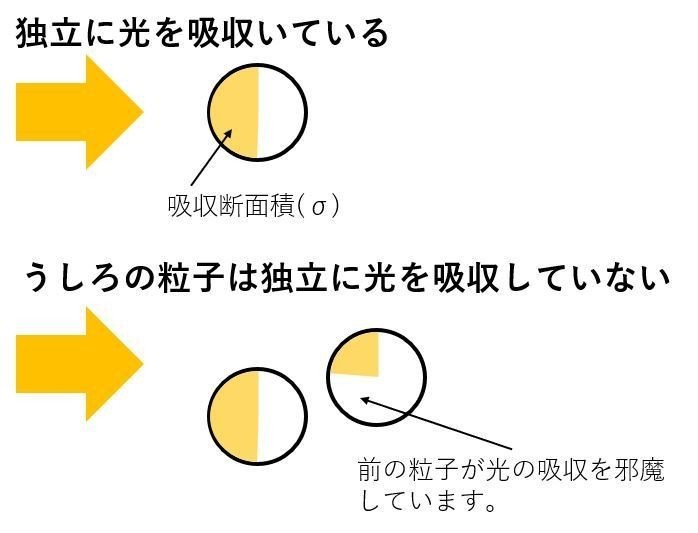
【独立した光を吸収する】というのは、前に粒子がおらずに、光を独立して吸収できることです。
そうでなければ、吸収断面積(σ)の値が小さく見積もられて、結果として濃度(ｃ)に対する吸光度(A)が小さな値として算出されることになります。

入射光に対して、10％しか透過光として出てこない条件を【独立した光を吸収】といえるでしょうか？
【独立に光を吸収】できるかどうかは、測定対象物の量が関係していますよね。測定対象物の量=濃度を下げれば、独立に光を吸収できる確率を上げることができます。