なぜ72を金利で割ると倍になる年数が分かるのか(ど文系対応、口語解説)
導入
こんにちは、金融界では便利&簡単な72の法則というものがあります。
72 ÷ 金利(%)= 2倍になる年数
というものです。
例えば金利が3%のとき、72 ÷ 3 = 24となり、投資後24年後に元本(投資額)が2倍になります。この法則は、かの有名なアインシュタインが発見しました。
また2倍では72のように、3倍のときには115の法則、4倍のときには144の法則もあります。
このようにシンプルな計算で複利の計算ができる素晴らしい法則です。しかし、72という数字はどこから現れたのでしょうか。
私は初めてこの法則を聞いたとき「なんで?」となり、深く理解するために調べましたがマクローリン展開だの収束半径だの言われ、しばらく数学に触れていない私にはチンプンカンプンでした。
ということで今回はなぜ72の法則が成り立つのか、高校レベルの数学で復習しながら解説します。
概要(計算式)
a: 金利、x: 年数とおきます。
金利が3%ならばa = 0.03です。

最後のlog e (1+a) = aとなる箇所以外は数2まででやる範囲ですので次の項目で述べます。理解できれば飛ばしても問題はありません。
逆に最後の箇所が一番難しく、なぜそうなるか調べても大学範囲のため理解が難しい方が過半数だと思います。その次の項目で直感的に、噛み砕いて解説します。
0.69が0.72になる理由はその後に解説します。
高校までの復習
まず始めの式立てについて説明します。
投資を開始した時点では資産額は変わりませんね、なので100%=1です。そしてそこにプラスされる金利がaであり、x年まで毎年1+a倍されるので指数にxをおきます。それが2倍になるので右の項には2がきます。
元手だけでなく金利も投入される複利のため、指数の式になるのです。
次に2番目の式になる理由です。求めたいのはxであり、このままでは指数であるxを求めることはできません。そのため、両辺をlog(対数)でくくってxを四則演算の域に下ろしてきます。
log(対数)とは指数を表すためのものでしたね。log ₃ 81 = 4。3を何乗したら81になるか、それは4です。というものでした。
logの便利な性質として、例にある81の部分を同値の9²(=81)にすると、
log ₃ 9²
= log ₃ 9 × 2
=2 × 2
= 4
という風に指数をlogの外の掛け算にすることができます。本題では指数はxでしたね。logでくくることによって、xを掛け算できるところまで持ってこれました。
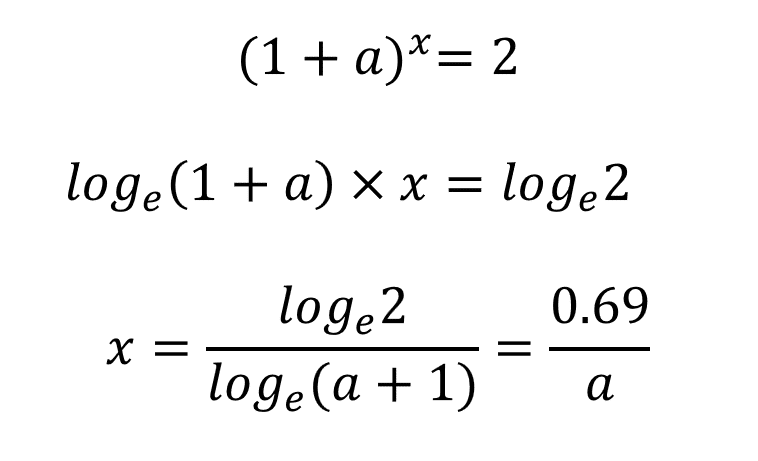
そして、対数の底(例の3の部分)はe(=2.71828182846…)にしています。そうすると便利なんです。底はなんでもいいのですが、計算しやすいためにeにしていると認識していただければ大丈夫です。
最後の式です。両辺をlog e (1+a) で割り、x = ? の形にできました。
ここで分子は
log e 2 ≒ 0.69
eを0.69乗すると2になるということです
(人力でやるとこれかなと模索しながらやることになり、超大変なので関数電卓でやります。電卓アプリを開いて横画面にするとできます。この豆知識も認知が広がりましたね、、)
そして分母はいきなりシンプルなaだけになってますが、、
log e (1+a) = a となる理由(本編)
最後のここが一番難しく、この記事を書く理由にもなった部分です。eをa乗すれば1+aになる、、かなり直感に反しています。まずは直感的に解説します。そのあとで難しい理屈を解説します。
視覚的にわかるように、y =log e (1+a)とy=aのグラフを書きます。これが同じ(近似)であれば、2つの式が等しい(近い)と分かりますね。
では、aが-10から10 (1000%)のときのy=log e (a+1)のグラフをどうぞ。

ここで前置きとして、金利であるaの範囲は-0.2から0.2くらいで考えます。実用的な金利は20%くらいまでしかありませんし、それ以上になると2倍の法則を使う意味がなくなってくるからですね。
異次元の金融緩和を行った国のために一応マイナス金利(0以下)も考えてあげていますね。その場合では何年前が2倍だったという感じです。
では、グラフの原点周りを拡大してy=aのグラフを並べてみましょう。
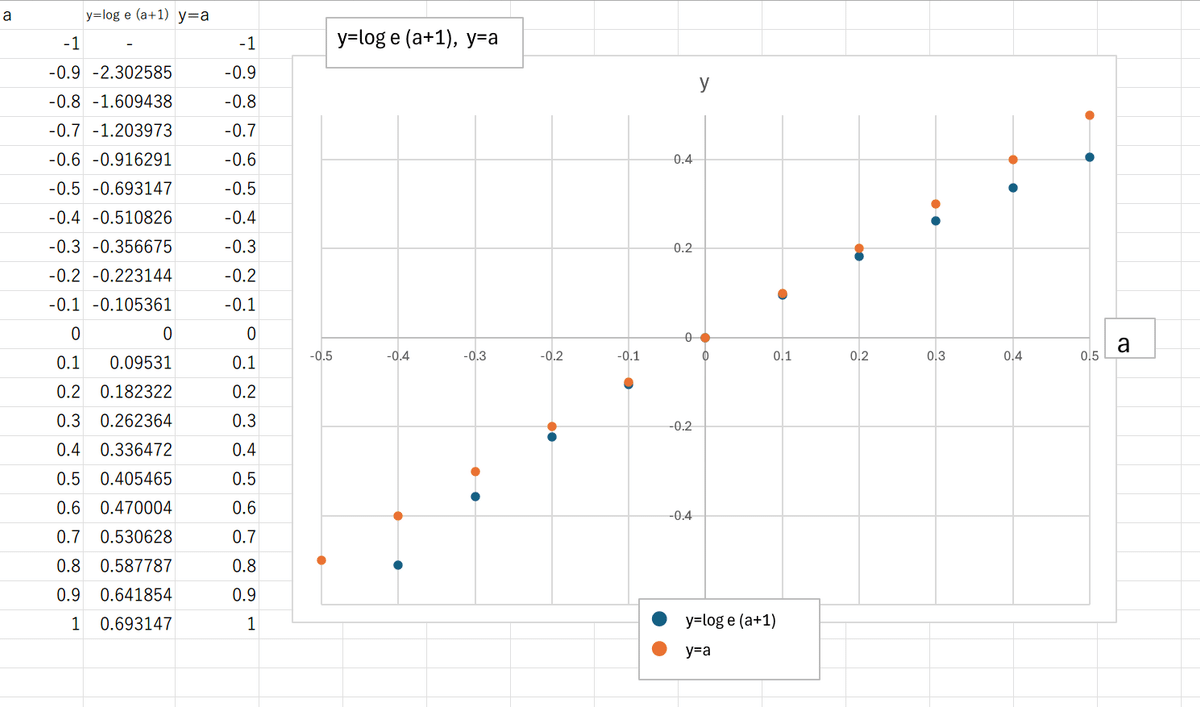
aの-0.2から0.2が範囲でしたね。原点に近づくにつれて青点と橙点が近づいていっていることがグラフから分かります。また、図左の数値表からも同じことが分かります。
ではさらに拡大して点同士を結んでみましょう。

0.02ずつ描いたので精度が上がっています。a = 0.1 (10%)以下になると誤差は5%を下回っていきます。
実用的な範囲でlog e (1+a) = aとなる理由は理解してもらえましたかね。
69なのに72になる??

最後にx = 69 ÷ 100a になり、100a は%表示から%を取り除けばいいので、
69 ÷ 金利(%の数字のまま)= 2倍になる年数
となりました。
なんで72になるんだよ!と思われるでしょうが、これには約数の数が関係しており、72では4や6など割り切れる数が多いため、便宜上そうなっているのです。本当は69の法則なんですね。金利が5%であれば70を割ってもいいでしょう。
72の理由はそれだけでなく、実際に投資する際、金利が変化することが多いことが挙げられます。そのための安全マージン(余裕)を持たせてるという意味合いもあります(多分)。
以上のカラクリで72が出てくるんですね。厳密に定めたい方にはストレスを与えてしまったと思いますが、計算のしやすさ > 数値のずれ という考えの法則なんでしょう(適当)。
なんで近似式が分かったの?(数3範囲、おまけ)
今までの解説では log e (1+a) = a になるらしいから、それを証明しようという流れでした。では、どうしてlog e (1+a) は aになると分かったのでしょうか。
y = log e (1+a)のグラフにおいて、 今回拡大した範囲である a = 0 あたりで近似する直線を求めましょう。
傾きを求めるときは微分をします。logの微分ってどうするんだっけ、、

y = log (1 + a) なので黒板のxが1+aに変わります。
ということで、
y' = 1 / (a + 1)
となります。
では微分できた式に a = 0 を代入しましょう。
y' = 1 / (0 + 1) = 1 / 1 =1
綺麗に傾きが1になりました。
傾きが1で、a =0 のとき、y = 0です。(どんな実数でも0乗すれば1になる)
ということで常にyとaが同じ式、 y = a という式が求まります。

aだけの直線よりa²(2次式)とか入れてより精密にした方がいいんじゃないの?と思って計算しようとするとテイラー展開(マクローリン展開)やら収束半径の話になります。テイラー展開は a²の2次式、a³の3次式、4次式、、、のように精密に式を出す展開です。展開された式を見て、実用的な範囲では1次式(y =a)までで十分だよねって分かる理由が収束半径にあるそうです。
あとがき、知識欲について
Excelの散布図(近似曲線には多項式近似=テイラー展開を用いています)とPowerPointの数式で説明できるものなんですね。Officeって万能なんだなと感心させられました。

知識欲に知識が追いついていない、、だからこそ私はlog e (1+a) = aの理由を調べても分からなかったし、自分なりに理解するのに苦戦しました。
ですが知識が追いついていなかったからこそ、自分なりの理解を生み出すことができ、同じ境遇の方に「同じ目線での」解説をすることができたと考えています。
なんで?なんで?と子どものように疑問を持つことは大人になっても知識面で役に立ちます。ですが、個人的には知識面による実利よりも興味関心による楽しさが人生を豊かにしてくれることに意義があると思っています。
分からないことが多い、何でも未知を知りたい子どもの世界ってとっても楽しいんですよね。それを大人になったからやめようというのはつまらない考え方だと思いませんか。