文系の文系による文系のための「相関行列」

機械学習で出てくる「相関行列」を調べましたのでなるべくわかりやすく説明します。
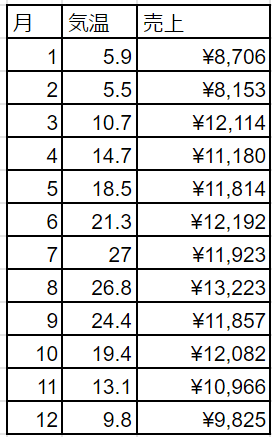
そして、実践として下記の気温とアイスクリームの売上げの相関行列をpythonで求めてみたいと思います。

相関

［名］(スル)二つのものが密接にかかわり合っていること。「相関する二国間の経済」

上のアイスクリームの例では表を見ると気温が上がるとアイスクリームの売上げも上がっていますね。
これを「正の相関」といいます。（下グラフ）

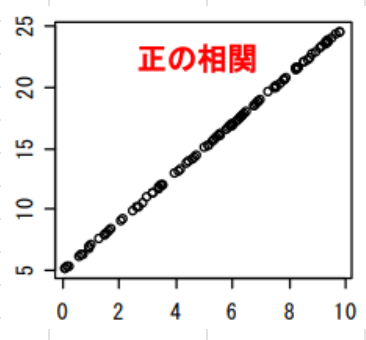
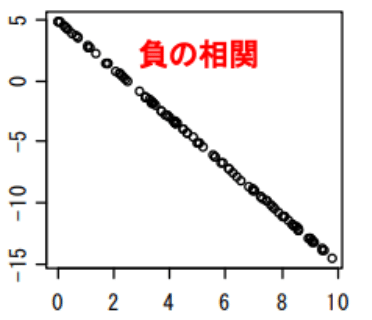
反対に負の相関もあり、これは一方が上がるともう一方が下がるものです。
例えば、気温が上がるとおでんの売上げが下がるとかです。（下グラフ）

【問題】相関の強さ

上の３つのグラフで一番相関が強いものはどれでしょうか？

正解は「一番左のグラフ」です。
真ん中のグラフや右のグラフはXが大きくなったときにYの大きくなる量がバラバラだったり、時には小さくなるものもありこれらは左のグラフと比較して弱い相関と言えます。

相関を客観的に表現する

では、もし真ん中のグラフのみ見せられた時、相関は強いと言いますか？
それとも相関は弱いと言いますか？
あるいは、右のグラフだけを見せられた時、相関があると言いますか？

相関のあり・なしが見た人の主観によるものでは統計は取れません。
そこで出てくるのが相関の強さを数値で表した「相関係数」です。
相関係数は -1 <= r <= 1 の範囲であらわされます。

【問題】相関が弱いと相関係数はいくつになるでしょうか？

正解は0です。
-1と迷ったかもしれませんが、-1は上で紹介した負の相関（強い）になります。
上で紹介した３つの正の相関の各相関係数は下記となります。

御覧の通り正の相関は相関が強いほど相関係数が大きく一次関数のようなグラフになります。

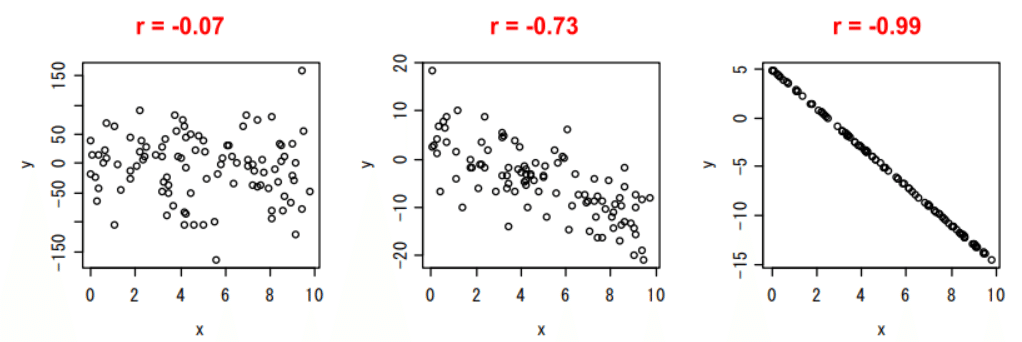
反対に負の相関は相関が強いほど相関係数が小さくなります。
相関についてイメージができたと思うので次のステップへ。

相関行列とは

まず行列とは名前の通り行と列で表現されたものであり、表とかエクセルとかをイメージしてもらえるとよいと思います。
そして、相関行列とは相関係数が行と列に並んでいることを言います。

#こんなイメージ
[[相関係数1, 相関係数2, 相関係数3, 相関係数4, 相関係数5],
 [相関係数6, 相関係数7, 相関係数8, 相関係数9, 相関係数10]
 ……
 ]

なんか急に難しくなったと感じると思いますが、もう少し読んでください。
これまでは気温とアイスクリームの売上げの相関と言ったように２つの要素だけに注目して相関を見ましたが、ここに湿度が加わった場合どうでしょうか。
湿度と売上げの相関も調べて、気温と売上げの相関と比べたりしませんか？
実際の統計では色々な要素の相関関係を見比べて売上げとの相関を分析します。
要素数が５個、１０個、２０個…と増えていくととてもじゃないけど要素の組み合わせを覚えられませんよね。そこで下のように総当たりの表で管理するとどの要素の組み合わせで相関を表しているかわかりやすいと思いませんか？
これが相関の行列です。

Pythonを使ってみる

では、Pythonでどうやって求めるのかやってみます。
初心に戻って気温と売上で見てみたいと思います。

ではPythonでやっていきます。Pythonではcorrcoef()というメソッドに相関行列を求めたい要素のリストを渡すことで計算できます。
下記ではcorrcoef()を使って求めた相関行列Rを出力しています。

import numpy as np
################# 1月  2月  3月   4月   5月   6月   7月   8月   9月   10月  11月  12月
R = np.corrcoef([[5.9, 5.5, 10.7, 14.7, 18.5, 21.3, 27.0, 26.8, 24.4, 19.4, 13.1, 9.8], #気温
               [8706,8153,12114,11180,11814,12192,11923,13223,11857,12082,10966,9825]]) #売上

print(R)

出力結果は下記の通りです

[[ 1.0  　　　0.83639953]
[ 0.83639953 1.0             ]]