
【東京都(東京都庁)Ⅰ類A】 事務 専門記述試験 過去問解説 経済原論(令和6年~平成22年)
このコンテンツでは、東京都1類Aの専門記述試験「経済原論」の過去問解説を詳しくご提供いたします。東京都1類Aは情報が非常に限られている試験ですが、本コンテンツでは他にはない充実した解説が含まれており、安心して試験対策を進めることができます。価格は少々お高めですが、その価値は十分にあります。市場には出回っていない貴重な情報をお届けしますので、ぜひご活用ください。
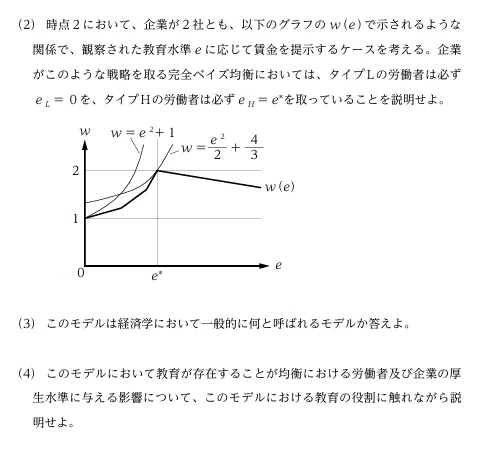
令和6年度
問題





解答
Ⅰ
生産関数は以下のように与えられる。
Y_t = (K_t)^{\alpha} (L_t)^{1 - \alpha}
ここで、Y_t は t 期の生産量、K_t は t 期の資本ストック、L_t は t 期の労働人口を表している。労働人口は一定であるとし、家計は所得のある一定割合 (1 - s) を消費すると仮定する。貯蓄率を 0 < s < 1 とし、資本の減耗率は 0 < δ < 1 とする。企業は利益を最大化する行動をとるとする。このとき、次の問いに答えよ。
(1) 一人当たり資本ストック k_t = K_t / L_t が時間を通じてどのように変化するか、資本蓄積の遷移式を求めよ。
解答:
一人当たり資本ストック k_t は以下のように定義される。
k_t = K_t / L_t
生産関数を一人当たりで表すと、
y_t = Y_t / L_t = k_t^{\alpha}
資本蓄積の遷移式は、
K_{t+1} = (1 - δ)K_t + sY_t
これを一人当たりの資本ストックに変換すると、
k_{t+1} = (1 - δ)k_t + s k_t^{\alpha}
したがって、資本蓄積の遷移式は以下のようになる。
k_{t+1} = (1 - δ)k_t + s k_t^{\alpha}
(2) この経済における定常状態を定義し、定常状態における一人当たり資本ストック、一人当たり生産量、一人当たり消費及び実質賃金を求めよ。
解答:
定常状態の定義:
定常状態では、一人当たり資本ストック k が時間を通じて変化しない状態を指す。
k_{t+1} = k_t = k^*
定常状態における資本蓄積の遷移式は、
k^* = (1 - δ)k^* + s (k^*)^{\alpha}
これを整理すると、
s (k^)^{\alpha} = δ k^
(k^*)^{\alpha - 1} = δ / s
k^* = (s / δ)^{1 / (1 - \alpha)}
一人当たり生産量:
y^* = (k^*)^{\alpha} = (s / δ)^{\alpha / (1 - \alpha)}
一人当たり消費:
一人当たり消費 c は生産量から貯蓄を引いたもの。
c^* = y^* - s y^* = (1 - s) y^*
実質賃金:
実質賃金 w は生産関数の労働に関する限界生産物で与えられる。
w = ∂Y / ∂L = (1 - \alpha) k^{\alpha}
したがって、定常状態における実質賃金は、
w^* = (1 - \alpha) (k^*)^{\alpha} = (1 - \alpha) (s / δ)^{\alpha / (1 - \alpha)}
(3) t - 1 期まで定常状態にあった経済において、t 期に戦争が勃発し、多くの労働者の命が失われ、t + 1 期以降、戦後の復興が開始されたとする。このとき、次の問いに答えよ。
(a) 一人当たり生産量は時間を通じてどのような変化をするか説明せよ。
解答:
戦争が勃発し、多くの労働者が失われた場合、労働人口 L_t が減少する。資本ストック K_t は変わらないため、一人当たり資本ストック k_t は増加する。したがって、一人当たり生産量 y_t = k_t^{\alpha} も一時的に増加する。
復興が進むにつれて、労働人口が徐々に回復し、再び定常状態に向かう。最終的には元の定常状態に戻る。
(b) 当初の定常状態と戦後に到達する定常状態ではどのような違いがあるか説明せよ。
解答:
戦争により労働人口が一時的に減少するが、復興が進むと労働人口は元に戻る。したがって、戦後に到達する定常状態は当初の定常状態と同じである。具体的には、一人当たり資本ストック k^、一人当たり生産量 y^、一人当たり消費 c^、実質賃金 w^ はすべて元の定常状態に戻る。
(4) 投資の調整コスト AC_t が存在し、以下で与えられるとする。
AC_t = \frac{\phi}{2} \left( \frac{I_t}{I_{t-1}} - 1 \right)^2 I_t
ここでは、I_t は t 期の投資額、\phi > 0 は投資の調整コストの大きさを表すパラメーターである。この場合、資本蓄積の遷移式は、
K_{t+1} = (1 - δ)K_t + I_t - AC_t
となる。他の条件は同一であるとして、投資の調整コストが高い H 国と低い L 国を比較する (\phi_H > \phi_L)。同じレベルの一人当たり資本ストックからスタートし、この二国が到達する定常状態と移行過程について何が言えるか説明せよ。
解答:
定常状態:
投資の調整コストが存在しない場合と同様に、定常状態では資本ストックが変化しないため、
K_{t+1} = K_t
I_t = δ K_t
調整コストの影響を考慮すると、
AC_t = 0
したがって、定常状態における資本蓄積の遷移式は変わらず、
K_{t+1} = (1 - δ)K_t + I_t
定常状態では、一人当たり資本ストック k^、一人当たり生産量 y^、一人当たり消費 c^、実質賃金 w^ はすべて同じである。
移行過程:
投資の調整コストが高い H 国 (\phi_H > \phi_L) では、投資の変動が大きくなると高いコストが発生するため、投資が調整される速度が遅くなる。したがって、H 国は新しい定常状態に到達するまでに時間がかかる。
一方、投資の調整コストが低い L 国 (\phi_L) では、投資の変動に対するコストが低いため、投資がスムーズに行われ、新しい定常状態に早く到達する。
II
政府は第1期の政府支出 G_1 を税収 T_1 と公債発行 B によって賄う。発行された公債は、利子率 r の利払いと共に第2期に全て償還される。政府の直面する予算制約式は、以下で与えられる。
G_1 = T_1 + B
G_2 + (1 + r) B = T_2
ここで、G_2 及び T_2 は第2期の政府支出及び税収を表している。
家計は、第1期と第2期の所得(Y_1 と Y_2)、利子率 r、政府の政策を所与として、効用を最大化するように各期の消費(C_t)を決定する。家計の効用関数は、以下のように与えられる。
U(C_1, C_2) = log(C_1) + β log(C_2)
ここでは、0 < β < 1 は主観的割引率を表す。家計は、各期 T_t の一括税を課税される。家計が直面している予算制約式は、
C_1 + S + B ≤ Y_1 - T_1
C_2 ≤ Y_2 - T_2 + (1 + r)(S + B)
となる。ここでは、S ≥ 0 は貯蓄を表し、B は公債の購入額となる。このとき、次の問いに答えよ。
(1) T_1 = T_2 = 0 の場合、第1期と第2期の最適な消費を求めよ。
まず、家計の予算制約式を T_1 = T_2 = 0 の条件で整理すると、
C_1 + S + B ≤ Y_1
C_2 ≤ Y_2 + (1 + r)(S + B)
となる。家計は効用最大化を行うため、ラグランジュ関数を用いて最適化問題を設定する。
L = log(C_1) + β log(C_2) + λ (Y_1 - C_1 - S - B) + μ (Y_2 + (1 + r)(S + B) - C_2)
このラグランジュ関数を C_1, C_2, S, B について偏微分し、最適化条件を求める。
∂L/∂C_1 = 1/C_1 - λ = 0
∂L/∂C_2 = β/C_2 - μ = 0
∂L/∂S = -λ + μ(1 + r) = 0
∂L/∂B = -λ + μ(1 + r) = 0
ここから、
λ = 1/C_1
μ = β/C_2
を代入して整理すると、
1/C_1 = β(1 + r)/C_2
これを変形すると、
C_2 = β(1 + r)C_1
予算制約式 C_1 + S + B = Y_1 と C_2 = Y_2 + (1 + r)(S + B) を代入すると、
C_1 + S + B = Y_1
β(1 + r)C_1 = Y_2 + (1 + r)(S + B)
S + B = Y_1 - C_1
代入して、
β(1 + r)C_1 = Y_2 + (1 + r)(Y_1 - C_1)
β(1 + r)C_1 = Y_2 + (1 + r)Y_1 - (1 + r)C_1
(β(1 + r) + (1 + r))C_1 = Y_2 + (1 + r)Y_1
(β + 1)(1 + r)C_1 = Y_2 + (1 + r)Y_1
C_1 = (Y_2 + (1 + r)Y_1) / ((β + 1)(1 + r))
C_2 = β(1 + r)C_1
(2) T_1, T_2 > 0 の場合、第1期と第2期の最適な消費を求めよ。
同様に、予算制約式を T_1, T_2 > 0 の条件で整理すると、
C_1 + S + B ≤ Y_1 - T_1
C_2 ≤ Y_2 - T_2 + (1 + r)(S + B)
となる。効用最大化のラグランジュ関数は同様に設定する。
L = log(C_1) + β log(C_2) + λ (Y_1 - T_1 - C_1 - S - B) + μ (Y_2 - T_2 + (1 + r)(S + B) - C_2)
同様に偏微分して最適化条件を求めると、
C_2 = β(1 + r)C_1
予算制約式を代入して、
C_1 + S + B = Y_1 - T_1
β(1 + r)C_1 = Y_2 - T_2 + (1 + r)(S + B)
S + B = Y_1 - T_1 - C_1
β(1 + r)C_1 = Y_2 - T_2 + (1 + r)(Y_1 - T_1 - C_1)
β(1 + r)C_1 = Y_2 - T_2 + (1 + r)Y_1 - (1 + r)T_1 - (1 + r)C_1
(β(1 + r) + (1 + r))C_1 = Y_2 - T_2 + (1 + r)Y_1 - (1 + r)T_1
(β + 1)(1 + r)C_1 = Y_2 - T_2 + (1 + r)Y_1 - (1 + r)T_1
C_1 = (Y_2 - T_2 + (1 + r)Y_1 - (1 + r)T_1) / ((β + 1)(1 + r))
C_2 = β(1 + r)C_1
(3) 政府が第1期に大幅な減税を行うとする。他の条件を一定とすると、第1期と第2期の消費にどのような影響を与えるか説明せよ。
第1期の減税により、T_1 が減少する。これにより第1期の可処分所得が増加し、C_1 が増加する。一方で、第2期に返済すべき公債発行額が増加し、T_2 が増加するため、第2期の可処分所得が減少し、C_2 が減少する。
(4) 政府が一括税の代わりに税率 0 < τ_1, τ_2 < 1 の消費税で徴税するとする。このとき、次の問いに答えよ。
(a) 第1期と第2期の最適な消費を求めよ。
消費税 τ_1, τ_2 を考慮すると、予算制約式は次のようになる。
(1 + τ_1)C_1 + S + B ≤ Y_1
(1 + τ_2)C_2 ≤ Y_2 + (1 + r)(S + B)
効用最大化のラグランジュ関数は同様に設定する。
L = log(C_1) + β log(C_2) + λ (Y_1 - (1 + τ_1)C_1 - S - B) + μ (Y_2 + (1 + r)(S + B) - (1 + τ_2)C_2)
同様に偏微分して最適化条件を求めると、
(1 + τ_2)β(1 + r)C_1 = (1 + τ_1)C_2
予算制約式を代入して、
(1 + τ_1)C_1 + S + B = Y_1
(1 + τ_2)β(1 + r)C_1 = Y_2 + (1 + r)(Y_1 - (1 + τ_1)C_1 - S - B)
S + B = Y_1 - (1 + τ_1)C_1
(1 + τ_2)β(1 + r)C_1 = Y_2 + (1 + r)(Y_1 - (1 + τ_1)C_1) - (1 + r)(S + B)
C_1 = (Y_2 + (1 + r)Y_1) / ((β + 1)(1 + r))
C_2 = (1 + τ_2)β(1 + r)C_1 / (1 + τ_1)
(b) 政府が第2期に消費税減税を行うとする。他の条件を一定とすると、第1期と第2期の消費にどのような影響を与えるか説明せよ。
第2期の消費税率 τ_2 が減少すると、C_2 の可処分所得が増加し、C_2 が増加する。第1期の消費税率 τ_1 が一定であれば、第1期の消費 C_1 には影響がない。しかし、第2期の消費が増加することで、家計の全体的な消費パターンが変わり、消費の割引価値も変動する可能性がある。
ここから先は
この記事が気に入ったらチップで応援してみませんか?
