【プログラミング初心者】が売上を予測してみました （vol.3 : 回帰編）

この記事は、週毎の売上分析、予測をまとめたものです。
内容は3部構成になっています。
vol.1 : データ整理編
vol.2 : 時系列解析編
vol.3 : 回帰編

今回は「vol.3 : 回帰編」です。

前回までのおさらい

「vol.1 : データ整理編」では、excelファイルのデータを整理し、csvデータに変換しました。「vol.2 : 時系列解析編」 では、SARIMAモデル・PROPHETモデルを用いて、時系列解析を行い、testデータに対しては、PROPHETモデルの方が SARIMAモデルよりも優れているということがわかりました。「vol.3 : 回帰編」ではさらに精度を比較するため、回帰モデルを作成したいと思います。

【線形重回帰】

線形重回帰を用いて回帰分析をしていきます。
線形重回帰は、アイデミープレミアムプランの「教師あり学習（回帰）」講座の「1.2.4 線形重回帰」で学習したモデルです。
重回帰分析とは、２つ以上の独立変数により、１つの従属変数を予測･説明しようとすることです。

データの読み込み

まずはデータを読み込みます。

import pandas as pd
A_data=pd.read_pickle("/content/drive/MyDrive/A_data.pkl")
train_data=pd.read_pickle("/content/drive/MyDrive/train_data.pkl")
A_data

「vol.2 : 時系列解析編」で、周期は週ごとのデータであることも考慮して、4週区切りとしました。その流れを引き継いで、回帰モデルでは4つのデータ（t, t-1, t-2, t-3)を1セットとして学習用データを作成します。
また​ t+1を予測するとし、教師データとします。

X=[]
y=[]
idx=4
for num in range(idx-1, len(A_data["A"])-idx):
 tmp_list=[]
 for i in range(idx):
   tmp_list.append(A_data.iloc[num-(idx-1) + i, 0])
 X.append(tmp_list)
 y.append(A_data.iloc[num+1, 0])

「vol.2 : 時系列解析編」にて119週までをtrainデータとし、120週から150週までをtestデータとしました。testデータは30週分です。
精度を検証するため、回帰モデルを作成する際も期間（予測対象数）を合わせます。

import numpy as np
X=np.array(X)
y=np.array(y)
num=int(X.shape[0]*0.8)
train_X=X[:num]
train_y=y[:num]
test_X=X[num:num+30]
test_y=y[num:num+30]

モデル作成

モデルを作成します。

from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(train_X, train_y)
# 決定係数の出力です
print(model.score(test_X, test_y))​

-0.1865278239571635

test_Xの中身を確認します。

test_X.shape

(30, 4)

回帰モデルでは、基本的に予測を行う対象はt+1としたので、それ以降も予測できるようにscore_predict関数を作成します。score_predict関数では、入力データ, 予測したいデータのステップ数を引数で指定することで、関数内部ではfor文を用いて予測が繰り返し行われます。

def score_predict(model, base, steps):
 scores= []
 for i in range(steps):
   t= model.predict(np.array([base]))
   base= np.hstack((base[1:], t[0]))
   scores.append(t[0])
 return np.array(scores)

score_predict(model, test_X[0], 10)

array([76390.16960366, 78224.0166397 , 78449.44197072, 83239.2595787 ,
83208.86282825, 84140.98678069, 84495.72172009, 85699.91394122,
86125.73152228, 86596.77044898])

グラフの可視化、二乗誤差の出力・精度確認

予測期間での予測値を代入しグラフを可視化します。
実際の売上は青色、予測値は赤色でプロットします。
同時に二乗誤差を出力し、精度を確認します。

import matplotlib.pyplot as plt
x = list(range(30))
y1= test_y[:30]
y2 = score_predict(model, test_X[0], 30)
# グラフの描画
plt.plot(x, y1,color="r")
plt.plot(x, y2)
plt.show()
#二乗誤差を出力し、精度を確認します。
from sklearn.metrics import mean_squared_error
Y_train_pred = model.predict(train_X) 
Y_test_pred = score_predict(model, test_X[0], 30)
print('MSE train data: ', mean_squared_error(train_y, Y_train_pred)) # 学習データを用いたときの平均二乗誤差を出力
print('MSE test data: ', mean_squared_error(test_y, Y_test_pred))         # 検証データを用いたときの平均二乗誤差を出力

MSE train data: 1221112749.7203033
MSE test data: 990164256.8432528

予測と実際の値にかなり差が出ています。
別の回帰モデルも作成してみたいと思います。

【ラッソ回帰】

ラッソ回帰を用いて回帰分析をしていきます。
ラッソ回帰は、アイデミープレミアムプランの「教師あり学習（回帰）」講座の「2.1.3 ラッソ回帰」で学習したモデルです。
ラッソ回帰とはL1正則化を行いながら線形回帰の適切なパラメータを設定する回帰モデルです。

モデル作成
グラフの可視化、二乗誤差の出力・精度確認

予測期間での予測値を代入しグラフを可視化します。
実際の売上は青色、予測値は赤色でプロットします。
同時に二乗誤差を出力し、精度を確認します。

from sklearn.linear_model import Lasso
model_l = Lasso()
model_l.fit(train_X, train_y)
print(model_l.score(test_X, test_y))
import matplotlib.pyplot as plt
x = list(range(30))
y1= test_y[:30]
y2 = score_predict(model_l, test_X[0], 30)
# グラフの描画
plt.plot(x, y1,color="r")
plt.plot(x, y2)
plt.show()
#二乗誤差を出力し、精度を確認します。
from sklearn.metrics import mean_squared_error
Y_train_pred = model_l.predict(train_X) 
Y_test_pred = score_predict(model_l, test_X[0], 30)
print('MSE train data: ', mean_squared_error(train_y, Y_train_pred)) # 学習データを用いたときの平均二乗誤差を出力
print('MSE test data: ', mean_squared_error(test_y, Y_test_pred))         # 検証データを用いたときの平均二乗誤

-0.18652782504751397

MSE train data: 1221112749.7203028
MSE test data: 990164257.460194

線形重回帰モデルと全く同じ結果が得られました。コードが間違っているのかと思い、何度か修正しましたが得られた結果は全く同じでした。ラッソ回帰は線形回帰に正則化項を加えた手法のため、基本的には同じ処理を行っているので全く同じ結果になることがあるようです。

【ランダムフォレスト】

ランダムフォレストを用いて分析をしていきます。
ランダムフォレストは、アイデミープレミアムプランの「教師あり学習（分類）」講座の「1.2.5 ランダムフォレスト」で学習したモデルです。
ランダムフォレストは、前述の決定木の簡易版を複数作り、分類の結果を多数決で決める手法です。複数の簡易分類器を一つの分類器にまとめて学習させる、 アンサンブル学習の一手法でもあります。
ランダムフォレストの特徴は、決定木と同じように、外れ値によって結果が左右されにくいことです。また、線形分離可能でない複雑な識別範囲を持つデータ集合の分類にも使えます。

モデル作成
グラフの可視化、二乗誤差の出力・精度確認

予測期間での予測値を代入しグラフを可視化します。
実際の売上は青色、予測値は赤色でプロットします。
同時に二乗誤差を出力し、精度を確認します。

from sklearn.ensemble import RandomForestRegressor
model = RandomForestRegressor(max_depth=2, random_state=0)
model.fit(train_X, train_y)
print(model.score(test_X, test_y))

import matplotlib.pyplot as plt
x = list(range(30))
y1= test_y[:30]
y2 = score_predict(model, test_X[0], 30)
# グラフの描画
plt.plot(x, y1,color="r")
plt.plot(x, y2)
plt.show()
#二乗誤差を出力し精度を確認します。
from sklearn.metrics import mean_squared_error
Y_train_pred = model.predict(train_X) 
Y_test_pred = score_predict(model, test_X[0], 30)
print('MSE train data: ', mean_squared_error(train_y, Y_train_pred)) # 学習データを用いたときの平均二乗誤差を出力
print('MSE test data: ', mean_squared_error(test_y, Y_test_pred))         # 検証データを用いたときの平均二乗誤差を出力

-0.32578945074021126

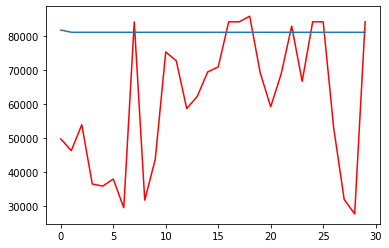
MSE train data: 822769885.1958103
MSE test data: 794316664.654536

こちらもあまりうまく学習ができていませんね、、
さらに別のモデルを作成してみたいと思います。

【XGBOOST】

XGBOOST用いて分析をしていきます。
XGBOOSTは、アイデミープレミアムプランの講座のなかでは学習しないのですが、発展的な内容としてチューターの先生に提案いただいたモデルです。
XGBOOSTとは、ブースティングと決定木を組み合わせた手法です。XGBOOSTは、誤差を予測するモデルです。１つ目の決定木では予測できなかった『誤差』を目的変数として、２つ目の決定木を構築することができます。

モデル作成
グラフの可視化、二乗誤差の出力・精度確認

予測期間での予測値を代入しグラフを可視化します。
実際の売上は青色、予測値は赤色でプロットします。
同時に二乗誤差を出力し、精度を確認します。

import xgboost as xgb
model = xgb.XGBRegressor()
model.fit(train_X, train_y)
print(model.score(test_X, test_y))
import matplotlib.pyplot as plt
x = list(range(30))
y1= test_y[:30]
y2 = score_predict(model, test_X[0], 30)
# グラフの描画
plt.plot(x, y1,color="r")
plt.plot(x, y2)
plt.show()
#二乗誤差を出力し、精度を確認します。
from sklearn.metrics import mean_squared_error
Y_train_pred = model.predict(train_X) 
Y_test_pred = score_predict(model, test_X[0], 30)
print('MSE train data: ', mean_squared_error(train_y, Y_train_pred)) # 学習データを用いたときの平均二乗誤差を出力
print('MSE test data: ', mean_squared_error(test_y, Y_test_pred))         # 検証データを用いたときの平均二乗誤差を出力

-0.7103202140780971

MSE train data: 131540433.9671928
MSE test data: 895148680.0246867

うーん、何とも言えない結果です。
最後にもう一つ試してみます。

【GRIDSERCH】

GRIDSERCHを用いて分析をしていきます。
GRIDSERCHは、アイデミープレミアムプランの「教師あり学習（分類）」講座の「3.4.1 グリッドサーチ」で学習したパラメーターセットを作成するために用いられる方法です。
https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.GridSearchCV.html

モデル作成
グラフの可視化、二乗誤差の出力・精度確認

予測期間での予測値を代入しグラフを可視化します。
実際の売上は青色、予測値は赤色でプロットします。
同時に二乗誤差を出力し、精度を確認します。

-0.26293081644591276

MSE train data: 537441859.0717394
MSE test data: 707148711.2297547

表示されたグラフの形は全く一致していないのですが、こちらのXGBOOSTをGRIDSERCHを使って一番いいパラメーターで調整したところ、一番精度が優れているという結果になりました。

【まとめ】

「vol.2 : 時系列解析編」 では、SARIMAモデル・PROPHETモデルを用いて、時系列解析を行い、testデータに対しては、PROPHETモデルの方が SARIMAモデルよりも優れているということがわかりました。
今回「vol.3 : 回帰編」では最後に作成したXGBOOSTをGRIDSERCHを使って一番いいパラメーターで調整したところ、一番精度が優れているという結果になりました。

PROPHETモデルとXGBOOSTの結果を比較すると、桁が多くてわかりづらいのですが、XGBOOSTの結果の方が精度が優れています。
よって今回作成したSARIMAモデル・PROPHETモデル・線形重回帰・ラッソ回帰・ランダムフォレスト・XGBOOSTのなかでは、XGBOOSTがもっとも精度が優れているいうことがわかりました。

作業時間ですが、回帰モデル5つの作成時間は約2時間でした。
時系解析モデルの作成時間は約2時間、データを揃えるのに約10時間、データの整理に約10時間かかったので、モデル作成においては、データの準備が多くの時間を占めているということがよくわかります。

時間をかけてさまざまな方法を試してきましたが、まだまだ実務に使える精度にはなっていないので、今後さらにデータを加えたり、分析の方法をかえることで売上予測の精度を上げていきたいです。
そして売上予測を在庫管理に活用し、売上向上とともに過剰在庫を削減する目標を達成するのがとても楽しみです。

さいごに

生粋の文系、数学ちんぷんかんぷんの私。作りたい成果物は決まっていましたが、私に作成できるのかとても不安でした。
はじめは外国語を勉強するような感覚でとにかくアイデミープレミアムプランの学習を進めました。slackでの質疑応答はもちろん、モデルの作成にあたり、チューターの先生には28回カウンセリングしていただきました。先生のご協力なくしては、このモデルは完成しなかったと思います。この場をかりてお礼申し上げます。
またこれからモデルのアップデートもしていきたいので、引き続きどうぞよろしくお願いします。

「vol.3 : 回帰編」はこちらで終わりです。
もしよければ、「vol.1 : データ整理編」「vol.2 : 時系列解析編」もあわせてぜひご覧くださいませ。
最後まで読んでいただき、ありがとうございました。