
【プログラミング初心者】が売上を予測してみました (vol.2:時系列解析編)
この記事は、週毎の売上分析、予測をまとめたものです。
内容は3部構成になっています。
vol.1 : データ整理編
vol.2 : 時系列解析編
vol.3 : 回帰編
今回は「vol.2 : 時系列解析編」です。
前回までのおさらい
「vol.1 : データ整理編」では、excelファイルのデータを整理し、csvデータに変換しました。「vol.2 : 時系列解析編」ではcsvデータを用いて、SARIMAモデル・PROPHETモデルを作成したいと思います。苦労して整えたデータがどのように活躍してくれるのか、とても楽しみです。
【SARIMAモデル】
SARIMAモデルを用いて時系列解析をしていきます。
SARIMAモデルは、アイデミープレミアムプランの「時系列解析Ⅰ(統計学的モデル)」講座のなかで学習したモデルです。
SARIMAモデルとは、ARIMAモデルをさらに季節周期を持つ時系列データにも拡張できるようにしたモデルです。 非定常過程のデータに対して適用できるのが大きな特徴です。
csvデータの読み込み
まずはcsvデータを読み込みます。
import pandas as pd
df= pd.read_csv("/content/drive/MyDrive/new_df.csv", index_col=0)
df
index指定
MD週の列が文字列になってしまっているため、このままでは使えないので取り扱いをしやすいindexに指定します。
時系列モデルでは、DATETIME型で入力が求められるので、DATETIME型のindexを作成しています。
index=pd.date_range("2018-03-05", "2021-02-28", freq="W")
indexDatetimeIndex(['2018-03-11', '2018-03-18', '2018-03-25', '2018-04-01',
'2018-04-08', '2018-04-15', '2018-04-22', '2018-04-29',
'2018-05-06', '2018-05-13',
...
'2020-12-27', '2021-01-03', '2021-01-10', '2021-01-17',
'2021-01-24', '2021-01-31', '2021-02-07', '2021-02-14',
'2021-02-21', '2021-02-28'],
dtype='datetime64[ns]', length=156, freq='W-SUN')
df.index=index
df
A-K店舗まで11店舗のデータがありますが、今回はA店舗のみ1店舗の売上を予測していきます。データは全部で156週分ありますが、学習に使用するデータとして120週分使用します。
A_data=df.drop(["MD週", 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K'], axis=1)
A_data_all = A_data
A_data=A_data.iloc[:120]
A_dataA
2018-03-11 86937
2018-03-18 120591
2018-03-25 127374
2018-04-01 113448
2018-04-08 93747
... ...
2020-05-24 5599
2020-05-31 17881
2020-06-07 84231
2020-06-14 63342
2020-06-21 51153
120 rows × 1 columns
モデル作成
今後データの取り扱いがしやすいよう、trainデータをpickleを使ってファイル化を行います。
SARIMAXクラスでは、オーダーとシーズナルオーダーを引数として指定する必要があります。https://www.statsmodels.org/stable/generated/statsmodels.tsa.statespace.sarimax.SARIMAX.html
これらを取得するために、selectparameter関数を実行します。
selectparameter関数は周期性を引数で指定する必要があります。今回のデータでは週毎のデータであることより、4が妥当であると思うため、4を指定します。
import warnings
import itertools
import pandas as pd
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt
# orderの最適化関数
def selectparameter(DATA, s):
p = d = q = range(0, 2)
pdq = list(itertools.product(p, d, q))
seasonal_pdq = [(x[0], x[1], x[2], s) for x in list(itertools.product(p, d, q))]
parameters = []
BICs = np.array([])
for param in pdq:
for param_seasonal in seasonal_pdq:
try:
mod = sm.tsa.statespace.SARIMAX(DATA,
order=param,
seasonal_order=param_seasonal)
results = mod.fit()
parameters.append([param, param_seasonal, results.bic])
BICs = np.append(BICs, results.bic)
except:
continue
return parameters[np.argmin(BICs)]
# 周期は週ごとのデータであることも考慮してs=4となります
# orderはselectparameter関数の0インデックス, seasonal_orderは1インデックスに格納されています
best_params = selectparameter(A_data, 4)
SARIMA_shop_sales = sm.tsa.statespace.SARIMAX(A_data.A, order=best_params[0],
seasonal_order=best_params[1],
enforce_stationarity=False, enforce_invertibility=False).fit()グラフの可視化
学習したモデルを使用し、予測期間を指定し予測値を可視化します。
実際の売上は青色、予測値は赤色でプロットします。
# predに予測期間での予測値を代入してください
pred = SARIMA_shop_sales.predict('2020-06-28', '2021-01-17')
# グラフを可視化してください。予測値は赤色でプロットしてください
plt.plot(A_data_all.iloc[120:])
plt.plot(pred, "r")
plt.show()
予測が進むにつれて、数値のズレが大きくなっていくのがわかります。
実際の予測された値を数値で見てみます。
pred2020-06-28 67491.470543
2020-07-05 59957.387466
2020-07-12 41226.138687
2020-07-19 42883.041112
2020-07-26 62842.889808
2020-08-02 55308.806731
2020-08-09 36577.557952
2020-08-16 38234.460377
2020-08-23 58194.309072
2020-08-30 50660.225995
2020-09-06 31928.977216
2020-09-13 33585.879641
2020-09-20 53545.728337
2020-09-27 46011.645260
2020-10-04 27280.396481
2020-10-11 28937.298906
2020-10-18 48897.147602
2020-10-25 41363.064525
2020-11-01 22631.815746
2020-11-08 24288.718171
2020-11-15 44248.566866
2020-11-22 36714.483789
2020-11-29 17983.235011
2020-12-06 19640.137436
2020-12-13 39599.986131
2020-12-20 32065.903054
2020-12-27 13334.654275
2021-01-03 14991.556700
2021-01-10 34951.405396
2021-01-17 27417.322319
Freq: W-SUN, dtype: float64
二乗誤差の出力、精度確認
二乗誤差を出力し、精度を確認します。
from sklearn.metrics import mean_squared_error
print('MSE train data: ', mean_squared_error(train_df_pred.A.values, train_y.values)) # 学習データを用いたときの平均二乗誤差を出力
print('MSE test data: ', mean_squared_error(A_data_all.iloc[120:150].A.values, pred.values)) # 検証データを用いたときの平均二乗誤差を出力
sarima_train_result= mean_squared_error(train_df_pred.A.values, train_y.values)
sarima_test_result= mean_squared_error(A_data_all.iloc[120:150].A.values, pred.values)MSE train data: 1646253544.7072015
MSE test data: 1300729991.4137871
精度がいいのか、はたまた悪いのかよくわからないです、、 他のモデルと比較をしてみたいと思います。
【PROPHETモデル】
PROPHETモデルを用いて時系列解析をしていきます。
PROPHETモデルは、アイデミープレミアムプランの講座のなかでは学習しないのですが、発展的な内容としてチューターの先生に提案いただいたモデルです。
PROPHETは、非線形トレンドが年次、週次、および日次の季節性に加えて休日の影響に適合する加法モデルに基づいて時系列データを予測するための手順です。これは、強い季節効果と数シーズンの履歴データを持つ時系列で最適に機能します。PROPHETは、欠測データやトレンドの変化に対して堅牢であり、通常、外れ値を適切に処理します。
https://facebook.github.io/prophet/docs/quick_start.html
モデル作成
trainデータを作成します。
PROPHETモデルでは、ターゲットをy、時系列をdsで指定します。
train_df=train_data
train_df.columns=["y"]
train_df.columns
train_df["ds"]=train_df.index
train_df
SARIMAモデルと比較するため、同様に120週から150週までをtestデータとしました。
test_data=A_data[120:150]
test_data.columns=["y"]
test_data.columns
test_data["ds"]=test_data.index
test_data.head()
trainデータを用いてモデルを学習させます。
from fbprophet import Prophet
model = Prophet()
model.fit(train_df)testデータを用いて予測を行います。
from sklearn.metrics import mean_squared_error
Y_test_pred = model.predict(test_data)
Y_train_pred= model.predict(train_df)表示のために、indexを合わせます。
Y_test_pred.index= test_data.index
グラフの可視化
先ほど求めた予測値を可視化します。
実際の売上は青色、予測値はオレンジ色でプロットします。
plt.plot(test_data.y,label = 'True')
plt.plot(Y_test_pred.yhat,label='Predict')
plt.legend()
こちらも予測が進むにつれてズレは大きくなっていますが、SARIMAモデルに比べると上がる、下がるの動きはつかめています。
二乗誤差の出力、精度確認
SARIMAモデルとの比較二乗誤差を出力し、精度を確認します。
print('MSE train data: ', mean_squared_error(train_df.y.values, Y_train_pred.yhat.values)) # 学習データを用いたときの平均二乗誤差を出力
print('MSE test data: ', mean_squared_error(test_data.y.values, Y_test_pred.yhat.values)) # 検証データを用いたときの平均二乗誤差を出力
prof_train_result= mean_squared_error(train_df.y.values, Y_train_pred.yhat.values)
prof_test_result= mean_squared_error(test_data.y.values, Y_test_pred.yhat.values)MSE train data: 796597849.654555
MSE test data: 1917269105.940969
【SARIMAモデルとPROPHETモデルの比較】
SARIMAモデルとPROPHETモデルの比較を行います。
予測を行うというプロセスが同条件で比較ができないのですが、同じ区間を予測した場合の精度を数値として確認していきます。
#SARIMAモデルとprophetモデルの比較を行います
if sarima_train_result < prof_train_result:
print("trainデータに対してPROPHETモデルのほうが精度がいいです", prof_train_result)
else:
print("trainデータに対してSARIMAモデルのほうが精度がいいです", sarima_train_result)
if sarima_test_result < prof_test_result:
print("testデータに対してPROPHETモデルのほうが精度がいいです", prof_test_result)
else:
print("testデータに対してSARIMAモデルのほうが精度がいいです", sarima_test_result)trainデータに対してSARIMAモデルのほうが精度がいいです 1646253544.7072015
testデータに対してPROPHETモデルのほうが精度がいいです 1917269105.940969
testデータに対しては、PROPHETモデルの方がSARIMAモデルよりも優れていることがわかりますね。
念の為、2つのモデルの差分も出してみます。
prof_test_result- sarima_test_result616539114.5271819
【標準化】
精度が上がる可能性があるので、学習用データを標準化してみます。
標準化は、アイデミープレミアムプランの「教師なし学習」講座のなかで学習した内容になります。各特徴量について平均が0、分散が1となるように変換します。こちらを標準化といいます。
標準化モデル作成
sklearnのStandardScalerのインスタンスを作成し、学習用データでfitさせます。fitさせた後、学習用データ、全データそれぞれに標準化処理を加えます。
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
ss.fit(A_data_all)
A_data_all_sd= ss.transform(A_data_all)
train_data_sd= ss.transform(train_data)train_data["A"]= train_data_sd
train_data_sd=train_data
A_data_all["A"]= A_data_all_sd
A_data_all_sd= A_data_alltrain_data_sd
パラメーターを設定します。
best_params = selectparameter(train_data_sd, 4)
SARIMA_shop_sales_sd = sm.tsa.statespace.SARIMAX(train_data_sd.A, order=best_params[0],
seasonal_order=best_params[1],
enforce_stationarity=False, enforce_invertibility=False).fit()グラフの可視化
PROPHETモデルと比較するため、120週から150週までをtestデータとします。testデータは30週分です。
予測期間での予測値を代入しグラフを可視化します。
実際の売上は青色、予測値は赤色でプロットします。
# predに予測期間での予測値を代入してください
pred = SARIMA_shop_sales_sd.predict('2020-06-21', '2021-02-21')
# グラフを可視化してください。予測値は赤色でプロットしてください
plt.plot(A_data_all_sd.iloc[118:])
plt.plot(pred, "r")
plt.show()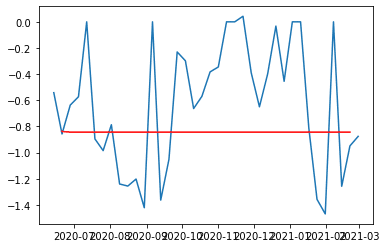
予測値が-0.8 から微動だにしていません、、
train_df_pred=A_data_all_sd.iloc[1:120]
train_y=SARIMA_shop_sales_sd.predict('2018-03-18', '2020-06-21')
pred= SARIMA_shop_sales_sd.predict('2020-06-28', '2021-01-17')二乗誤差の出力、精度確認
念の為二乗誤差を出力し、精度を確認します。
from sklearn.metrics import mean_squared_error
print('MSE train data: ', mean_squared_error(train_df_pred.A.values, train_y.values)) # 学習データを用いたときの平均二乗誤差を出力
print('MSE test data: ', mean_squared_error(A_data_all_sd.iloc[120:150].A.values, pred.values)) # 検証データを用いたときの平均二乗誤差を出力
sarima_train_result= mean_squared_error(train_df_pred.A.values, train_y.values)
sarima_test_result= mean_squared_error(A_data_all_sd.iloc[120:150].A.values, pred.values)MSE train data: 0.8846531979067381
MSE test data: 0.2928238647024817
うーん、こちらはあまりうまくいきませんでした。
時系列解析モデルにおいて、testデータに対しては、PROPHETモデルの方が SARIMAモデルよりも優れているということがわかりました。
まだまだ精度を比較していきたいので、時系列解析に続けてさらに回帰モデルも試してみたいと思います。
ふりかえり
時間の経過に伴い変化するデータという点を踏まえて、時系列解析をまず試してみました。周期は週ごとのデータであることも考慮して、4週区切りとしています。8週、16週も試してみたのですが、一番精度が高かった4週を選びました。
作業時間ですが、時系解析モデルの作成時間は約2時間でした。
trainデータとtestデータの期間指定を何パターンか試してみたので、少し検証の時間がかかりましたが、データ整理に比べるとかなりスムーズに進んだように思います。
最後まで読んでいただき、ありがとうございます。
「vol.2 : 時系列解析編」はこちらで終わりです。
続きは「vol.3 : 回帰編」です。「vol.1 : データ整理編」と合わせて、こちらもぜひご覧くださいませ。
